verilog booth编码乘法器

Booth编码

首先介绍一下波斯编码，可以通过理解下面的等式：
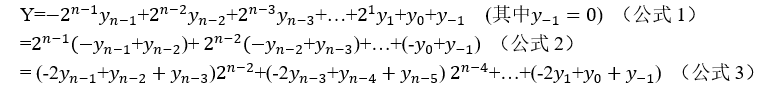可以证明的是，这三个公式是相等的，一个有符号的二进制数的补码用公式1来表示，可以等价地写成公式2和公式3。公式2其实就对应的2位一组的booth编码，公式3对应的3位一组的booth编码
这个过程就是对Y进行编码的过程。编码之后，乘数Y中的位被划分为不同的组， 每一组包括3位，这些组互相交叠。
Booth编码可以减少部分积的数目（即减少乘数中1的个数），用来计算有符号乘法，提高乘法运算的速度。

如上图所示为二进制乘法的过程，也是符合我们正常计算时的逻辑，我们假设有一个8位乘数（Multiplier），它的二进制值为0111_1110，它将产生6行非零的部分积，因为它有6个非零值（即1）。如果我们利用公式2：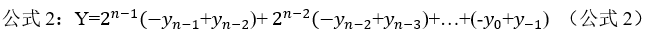
将这个二进制值改为1000_00-10，其中低四位中的-1表示负1，可以证明两个值是相等的。
这个变换过程可以这样简单理解，那就是在原值的末尾加辅助位0，变为0111_1110_0，然后利用低位减去高位，就对应-yn-1+yn-2，即得到1000_00-10。其实也对应公式2的对应编码，这样一变换可以减少0的数目，从而减少加的次数，我们只需相加两个部分积，但是最终的加法器必须也能执行减法。这种形式的变换称为booth encoding（即booth编码），它保证了在每两个连续位中最多只有一个是1或-1。部分积数目的减少意味着相加次数的减少，从而加快了运算速度（并减少了面积）。从形式上来说，这一变换相当于把乘数变换成一个四进制形式。波斯编码过程如下：

我们以6*14为例，对booth乘法运算进行举例：6的有符号二进制表示为00110，14的有符号二进制表示为01110，01110的booth编码表示为100-10，乘累加结果表示为P：

对应的verilog 代码如下：

`timescale 1ns / 1p
module booth_mult#(parameter D_IN=8)(
     input clk,
     input rst_n,
     
     input start,
     input [D_IN-1:0]mul_A,
     input [D_IN-1:0]mul_B,
     
     output reg done,
     output reg [2*D_IN-1:0]Product     
);
     
     reg [1:0]                    state;
     reg [2*D_IN-1:0]            mult_A;  // result of mul_A
     reg [D_IN:0]                mult_B;  // result of mul_A
     reg [2*D_IN-1:0]            inv_A;  // reverse result of mul_A
     reg  [2*D_IN-1:0]            result_tmp;  // operation register 
     wire [1:0]                    booth_code;
     assign booth_code = mult_B[1:0];
     assign stop=(~|mult_B)||(&mult_B);

     always @ ( posedge clk or negedge rst_n )
        if( !rst_n ) begin
            state <= 0;
            mult_A <= 0;
            inv_A <= 0;
            result_tmp  <= 0;
            done <= 0;
            Product<=0;
        end
        else if( start )
            case( state )    
                0: begin 
                    mult_A <= {{D_IN{mul_A[D_IN-1]}},mul_A}; 
                    inv_A <= ~{{D_IN{mul_A[D_IN-1]}},mul_A} + 1'b1 ; 
                    result_tmp <= 0; 
                    mult_B <= {mul_B,1'b0};
                    state <= state + 1'b1; 
                end
                1: begin
                    if(~stop) begin 
                         case(booth_code)
                            2'b01 : result_tmp <= result_tmp + mult_A;
                            2'b10 : result_tmp <= result_tmp + inv_A;
                            default: result_tmp <= result_tmp;
                        endcase 
                        mult_A <= {mult_A[14:0],1'b0};
                        inv_A <=  {inv_A[14:0],1'b0};
                        mult_B <= {mult_B[8],mult_B[8:1]};
                    end
                    else 
                        state <= state + 1'b1;
                end
                2:begin
                    done<=1'b1;
                    Product<= result_tmp;
                    state <= state+1;
                end
                3: begin
                    done<=1'b0;
                    state<=0;
                end
            endcase
endmodule

下面是仿真对应的testbench：

`timescale 1ns / 1ps
module tb_multi_seq();

    reg clk;
    reg rst_n;
     
    reg start;
    reg [7:0]mul_A;
    reg [7:0]mul_B;

    wire done;
    wire [15:0]Product;
     
   always #10 clk = ~clk;
    initial begin      
        rst_n = 0;         
        clk = 1;
        #10; 
        rst_n = 1;
     end
  booth_mult#(.D_IN(8)) 
    U1 (
        .clk(clk),
        .rst_n(rst_n),
        .start(start),
        .mul_A(mul_A),
        .mul_B(mul_B),
        .done(done),
        .Product(Product)
    );
     /***********************************/
    reg [3:0]i;
    always @ ( posedge clk or negedge rst_n )
        if( !rst_n )
            begin
                i <= 4'd0;
                start <= 1'b0;
                mul_A <= 8'd0;
                mul_B <= 8'd0;             
            end                
        else 
            case( i )
                0: // mul_A = 10 , mul_B = 2
                if( done ) begin start <= 1'b0; i <= i + 1'b1; end
                else begin mul_A <= 8'd10; mul_B <= 8'd2; start <= 1'b1; end
                
                1: // mul_A = 2 , mul_B = 10
                if( done ) begin start <= 1'b0; i <= i + 1'b1; end
                else begin mul_A <= 8'd2; mul_B <= 8'd10; start <= 1'b1; end
                
                2: // mul_A = 11 , mul_B = -5
                if( done ) begin start <= 1'b0; i <= i + 1'b1; end
                else begin mul_A <= 8'd11; mul_B <= 8'b11111011; start <= 1'b1; end
                
                3: // mul_A = -5 , mul_B = -11
                if( done ) begin start <= 1'b0; i <= i + 1'b1; end
                else begin mul_A <= 8'b11111011; mul_B <= 8'b11110101; start <= 1'b1; end
                
                4: begin i <= 4'd4; end
            endcase
 endmodule

以及仿真波形图
2bit编码比较简单，接下来可以继续进行3bit 编码的booth编码乘法器。