SLAM十四讲作业2

熟悉 Eigen 矩阵运算

5. 编程实现 A 为 100 * 100 随机矩阵时，⽤ QR 和 Cholesky 分解求 x 的程序

QR分解代码:

#include <iostream>
using namespace std;
#include <ctime>

// Eigen 部分
#include <Eigen/Core>

// 稠密矩阵的代数运算（逆，特征值等）
#include <Eigen/Dense>

// Eigen 固定⼤⼩矩阵最⼤⽀持到50
#define MATRIX_SIZE 50

const int N = 100;

int main(){
    // 矩阵大小超过50，使用动态矩阵
    Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > A;
    Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > Q,R;
    Eigen::HouseholderQR<Eigen::MatrixXd> QR;

    A = Eigen::MatrixXd::Random(N,N);

    QR.compute(A);
    
    Q = QR.householderQ();
    R = QR.matrixQR().triangularView<Eigen::Upper>();

    cout << "QR2(): HouseholderQR-----------------------------------"<< std::endl;
    //cout << "A "<< endl <<A << endl << endl;
    //cout << "Q "<< endl <<Q << endl << endl;
    //cout << "R "<< endl <<R << endl << endl;

    return 0;
}

Cholesky 分解

#include <iostream>
#include <cstdlib>
#include <ctime>
#include <time.h>

using namespace std;

// Eigen 部分
#include <Eigen/Core>

// 稠密矩阵的代数运算（逆，特征值等）
#include <Eigen/Dense>

// LLT LDLT
#include <Eigen/Cholesky>
using namespace Eigen;

// Eigen 固定⼤⼩矩阵最⼤⽀持到50
#define MATRIX_SIZE 50

const int N = 100;

int main(){
    cout<<"----------------way1----------------"<<endl;
    // 用A = LLt 生成元素都为正的下三角矩阵即可生成随机正定矩阵
    Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > U;
    U = Eigen::MatrixXd::Random(N,N);
    for(int i=0;i<N;i++){
        for(int j=i;j<N;j++){
            if(U(i,j)<=0){
                U(i,j) = -U(i,j) + 1;
            }
        }
        for(int j=0;j<i;j++){
            U(i,j)=0;
        }
    }
    cout << U << endl;

    Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > L = U.transpose();

    cout <<"--------L--------"<<endl;
    cout<<L<<endl;

    Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > A = L*U;

    cout <<"--------A--------"<<endl;
    cout<<A<<endl;

    LLT<MatrixXd> lltOfA(A); // compute the Cholesky decomposition of A
    MatrixXd Lcal = lltOfA.matrixL(); 

    cout <<"--------计算出来的L--------"<<endl;
    cout<<Lcal<<endl;

    cout<<"----------------way2----------------"<<endl;
    Matrix< double, Eigen::Dynamic, Eigen::Dynamic > X,Xsym,A2;
    X = MatrixXd::Random(N,N);

    Xsym = (X+X.transpose());

    Matrix< double, Eigen::Dynamic, Eigen::Dynamic > I = MatrixXd::Identity(N, N);
    A2 = Xsym + N*I;

    cout <<"--------计算出来的A2--------"<<endl;
    cout<<A2<<endl;

    LLT<MatrixXd> lltOfA2(A2); // compute the Cholesky decomposition of A
    MatrixXd Lcal2 = lltOfA2.matrixL(); 

    cout <<"--------计算出来的L2--------"<<endl;
    cout<<Lcal2<<endl;

    cout <<"--------验证A2--------"<<endl;
    cout<<Lcal2*Lcal2.transpose()<<endl;

    return 0;
}

几何运算练习

key : 使⽤Eigen/Geometry
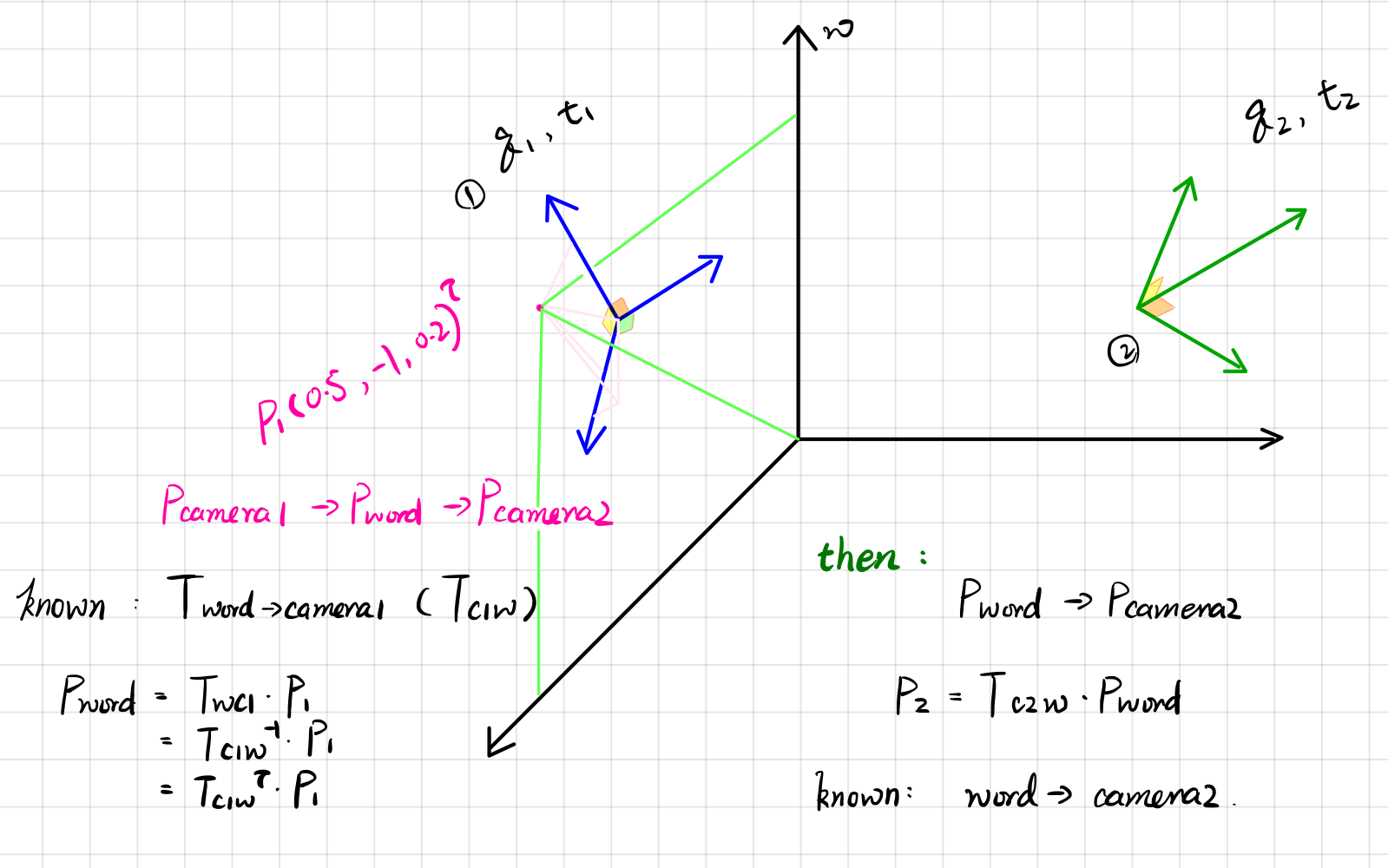
  设有⼩萝⼘⼀号和⼩萝⼘⼆号位于世界坐标系中。
  ⼩萝⼘⼀号的位姿为：\(q1 = [0.55, 0.3, 0.2, 0.2]; t1 =[0.7, 1.1, 0.2]^T\)（q 的第⼀项为实部）。这⾥的q 和t 表达的是\(T_{cw}\)，也就是世界到相机的变换关系。
  ⼩萝⼘⼆号的位姿为 \(q2 = [-0.1, 0.3,-0.7, 0.2]; t2 = [-0.1, 0.4, 0.8]^T\) 。
  现在，⼩萝⼘⼀号看到某个点在⾃⾝的坐标系下，坐标为 \(p1 = [0.5, -0.1, 0.2]^T\)，求该向量在⼩萝⼘⼆号坐标系下的坐标。请编程实现。

欧式群

\[\operatorname{SE}(3)=\left\{\boldsymbol{T}=\left[\begin{array}{cc}\boldsymbol{R} & \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1\end{array}\right] \in \mathbb{R}^{4 \times 4} \mid \boldsymbol{R} \in \operatorname{SO}(3), \boldsymbol{t} \in \mathbb{R}^{3}\right\} \]

注 :

1. 四元数在使⽤前需要归⼀化

#include <iostream>
#include <cstdlib>
#include <ctime>
#include <time.h>

using namespace std;


// Eigen 部分
#include <Eigen/Core>

// 稠密矩阵的代数运算（逆，特征值等）
#include <Eigen/Dense>

// LLT LDLT
#include <Eigen/Cholesky>
// 几何运算
#include<Eigen/Geometry>
using namespace Eigen;

int main(){
    Quaterniond q1(0.55,0.3,0.2,0.2);//定义四元数Q1
    Quaterniond q2(-0.1,0.3,-0.7,0.2);

    // 归一化
    q1.normalize();
    q2.normalize();

    Vector3d t1(0.7,1.1,0.2),t2(-0.1,0.4,0.8),p1(0.5,-0.1,0.2);// Vector3d 实质上是 Eigen::Matrix<double, 3, 1>

    Isometry3d T_c1w= Isometry3d::Identity();// word -> camera1 
    Isometry3d T_c2w= Isometry3d::Identity();// word -> camera2

    T_c1w.rotate(q1.toRotationMatrix());//四元数转化为旋转矩阵
    T_c1w.pretranslate ( t1 );
    // cout<<T_cw1.matrix() << "\n";

    T_c2w.rotate(q2.toRotationMatrix());//四元数转化为旋转矩阵
    T_c2w.pretranslate ( t2 );

    Vector3d p_word;
    p_word = T_c1w.inverse()*p1;
    // cout << p_word<< "\n";

    Vector3d p2;
    p2 = T_c2w*p_word;

    cout << p2 << endl;

    return 0;
}

旋转的表达

  课程中提到了旋转可以⽤旋转矩阵、旋转向量与四元数表达，其中旋转矩阵与四元数是⽇常应⽤中常见的表达⽅式。
  完成下述内容的证明。

1. 设有旋转矩阵\(R\),证明\(R^TR = I\)且 \(det(R) = +1\)
2. 设有四元数 \(q\)，我们把虚部记为\(\varepsilon\)，实部记为 \(\eta\)，那么 \(q = (\varepsilon , \eta)\)。请说明 \(\varepsilon\) 和 \(\eta\) 的维度。
3. 定义运算 + 和 \(\oplus\)为：

\[q^{+}=\left[\begin{array}{cc} \eta 1+\varepsilon^{\times} & \varepsilon \\ -\varepsilon^{\mathrm{T}} & \eta \end{array}\right], \quad \boldsymbol{q}^{\oplus}=\left[\begin{array}{cc} \eta \mathbf{1}-\varepsilon^{\times} & \varepsilon \\ -\varepsilon^{\mathrm{T}} & \eta \end{array}\right] \]

    其中运算 \(\times\)含义与 ^ 相同，即取 \(\varepsilon\) 的反对称矩阵（它们都成叉积的矩阵运算形式），\(1\) 为单位矩
阵。
    证明对任意单位四元数 \(q_1, q_2\)，四元数乘法可写成矩阵乘法：

\[q_1q_2 = q_1^{+}q_2 \]

或者

\[q_1q_2 = q_2^{\oplus}q_1 \]