2020牛客暑期多校训练营（第七场）补题

B. Mask Allocation

题意

有$n \cdot m$个口罩，现在问你怎样分配使得口罩既能全部平均分给$n$个医院，也能全部平均分配给$m$个医院。求出最少的盒子数，并且按照字典序大的结果输出

思路

比赛时想到一个画正方形的思路，盒子数即$n \cdot m$的大矩形能由最少正方形组成，取正方形对应的边长的和

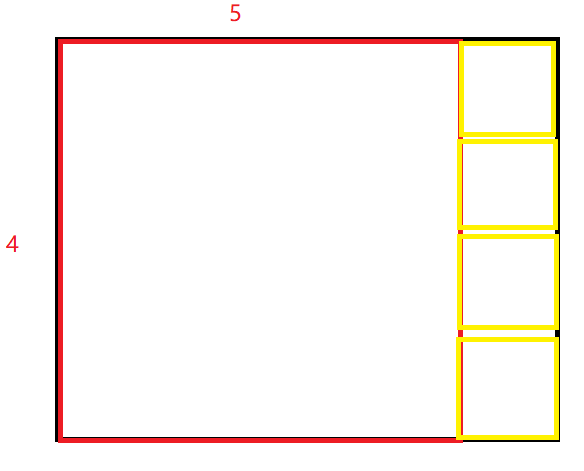
如图为样例5 4，显然盒子数为$4 \times 1 + 1 \times 4 = 8$

然后观察发现这不就是每次都在当前区域取$\lfloor m \div n \rfloor$个以$n$(假设m > n)为边长的正方形

余下的区域为$m \% n$$ \times n$，重复上述操作直到区域为0

可以用一个记忆划搜索来做，和gcd有异曲同工之妙，

输出也是一个问题，但是没有关系(杰哥nb!!)，递归输出一遍即可

代码

/*************************************************************************
 > FileName:
 > Author:      Lance
 > Mail:        lancelot_hcs@qq.com
 > Date:        9102.1.8
 > Description:
 ************************************************************************/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const double pi = acos(-1.0);
const double eps = 1e-6;
const int mod = 1e9 + 7;
#define debug(a) cout << "*" << a << "*" << endl
const int INF = 0x3f3f3f3f;//int2147483647//ll9e18//unsigned ll 1e19
const int maxn = 1000005;
//sacnf("%lf") printf("%f")
ll read() {
    ll x = 0,f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
        f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}

int t, n, m, flag;
int dp[10005][10005];

int dfs(int m, int n) {
    if (n == 0) return 0;
    if (dp[m][n]) return dp[m][n];
    else return dp[m][n] = dfs(n, m % n) + m / n * n;
}

void print(int m, int n) {
    if (n == 0) return;
    int all = m / n * n;
    for (int i = 0; i < all; i++)
        if (flag == 0) {
            printf("%d", n);
            flag = 1;
        } else printf(" %d", n);
    print(n, m % n);
}
 
void solve() {
    scanf("%d", &t);
    while (t--) {
        flag = 0;
        n = read(), m = read();
        if (m < n) swap(m, n);
        ll s = m / n;
        ll yu = m % n;
        if (yu == 0) {
            printf("%d\n", m / n * n);
            for (int i = 0; i < m; i++)
                if (i == 0) printf("%d", n);
                else printf(" %d", n);
            puts("");
        } else {
            ll ans = dfs(m, n);
            printf("%lld\n", ans);     
            print(m, n);
            puts("");
        }
    }
}
 
int main() {
//    freopen("F:/Overflow/in.txt","r",stdin);
//    ios::sync_with_stdio(false);
    solve();
    return 0;
}

H. Dividing

题意

给定n和k的取值范围，问有多少个合法的二元组，满足题目条件

思路

根据题目的意思，可以发现当且仅当n = 1 或n为k的倍数或n - 1为k的倍数时，(n, k)满足题目条件

n = 1时，有N + K - 1个

然后分别讨论n为k的倍数和n - 1为k的倍数的情况

n是k的倍数，$n=x\cdot k$，因为$n \leq 10^{12}$，那么可以减掉(x-1)个k，将n变为k，再/k为1

n - 1为k的倍数，同理

计算步骤

$\sum_{k=1}^{K} \sum_{n=1}^{N}(n \% k=0|| n \% k=1) \Rightarrow \sum_{k=2}^{K} \frac{n}{k}+\sum_{k=2}^{K}\left(\frac{n-1}{k}\right) + K + N - 1$

然后解锁一个数论分块的知识盲区

面对这样一个问题

\[\sum_{i=1}^{n}\left\lfloor\frac{n}{i}\right\rfloor \]
可以选择用O(n)的复杂度去暴力求解，但我们可以发现$n\div i$的值在某一段中是相等的，比方说5/ 3， 5/ 4 ，5/5的大小都为1，所以可以用这一段的长度Len 乘以这一段的值就是可以快速求和。
int ans = 0;
for(int l = 1, r = 0; l <= n; l = r + 1) {
    r = n / (n / l);  			// 求区间的右端，这是一个数学规律 
    ans += (r - l + 1) * (n / l);
} 

代码

/*************************************************************************
 > FileName:
 > Author:      Lance
 > Mail:        lancelot_hcs@qq.com
 > Date:        9102.1.8
 > Description:
 ************************************************************************/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const double pi = acos(-1.0);
const double eps = 1e-6;
const int mod = 1e9 + 7;
#define debug(a) cout << "*" << a << "*" << endl
const int INF = 0x3f3f3f3f;//int2147483647//ll9e18//unsigned ll 1e19
const int maxn = 1000005;
//sacnf("%lf") printf("%f")
ll read()
{
    ll x = 0,f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
	{
		if (ch == '-')
		f = -1;
		ch = getchar();
	}
    while (ch >= '0' && ch <= '9')
	{
		x = x * 10 + ch - '0';
		ch = getchar();
	}
    return x * f;
}
ll t, n, N, K, ans = 0;

void solve()
{
	N = read(), K = read();
	// n是k的倍数 n=xk
	for (ll i = 2, j; i <= K; i = j + 1) {
		ll x = N / i;
		if (x == 0) break;
		j = N / x;
		ans = (ans + ((min(j, K) - i + 1) % mod * (x % mod))) % mod;
	}
	// n-1是k的倍数 n=xk+1
	for (ll i = 2, j; i <= K; i = j + 1) {
		ll x = (N - 1) / i;
		if (x == 0) break;
		j = (N - 1) / x;
		ans = (ans + ((min(j, K) - i + 1)) % mod * (x % mod)) % mod;
	}
	ans = (ans + N + K - 1) % mod;
	cout << ans << '\n';
}

int main()
{

//    freopen("F:/Overflow/in.txt","r",stdin);
//    ios::sync_with_stdio(false);
    solve();
    return 0;
}

J. Pointer Analysis

J. Pinter Analysis

题意

四种赋值操作分别为，

Uppercase = Uppercase

Uppercase = Lowercase

Uppercase. Lowercase = Uppercase

Uppercase = Uppercase. Lowercase

给定n条赋值语句，可以通过任意顺序，次数来执行这些赋值语句，问每一个普通变量所能指向的最大对象集合

思路

理解了两种思路:

模拟

用每个大写字母对象集合可以用set存储

其中set $SS[i]$用来存储i的对象集合

set $amore[i][j]$用来存储i.j的对象集合

按上面的四种情况分类处理

内部循环可控制在26以内，故复杂度为$O\left(N^{2}\right)$

状压

代码

/*************************************************************************
 > FileName:
 > Author:      Lance
 > Mail:        lancelot_hcs@qq.com
 > Date:        9102.1.8
 > Description:
 ************************************************************************/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const double pi = acos(-1.0);
const double eps = 1e-6;
const int mod = 1e9 + 7;
#define debug(a) cout << "*" << a << "*" << endl
const int INF = 0x3f3f3f3f;//int2147483647//ll9e18//unsigned ll 1e19
const int maxn = 250;
//sacnf("%lf") printf("%f")
ll read()
{
    ll x = 0,f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
        f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
 
int t, n;
struct node {
    string s_1, equal, s_2;
}N[maxn];
 
struct SET {
    set<char> S;
}SS[70];
set<char> amore[70][70];
 
inline bool check_low(char c) {
    return c >= 'a' && c <= 'z';
}
 
void solve()
{
    int n;
    n = read();
    for (int i = 0; i < n; i++) cin >> N[i].s_1 >> N[i].equal >> N[i].s_2;
    for (int j = 0; j < n; j++) {
        for (int i = 0; i < n; i++) {
            int l1 = N[i].s_1.size(), l2 = N[i].s_2.size();
            int tem_1 = N[i].s_1[0] - 'A', tem_2 = N[i].s_2[0] - 'A';
            if (l1 == 1 && l2 == 1) {
             
                if (check_low(N[i].s_2[0])) {
                    SS[tem_1].S.insert(N[i].s_2[0]);
                } else {
                    for (auto it : SS[tem_2].S) {
                        SS[tem_1].S.insert(it);
                    }
                }
            } else { // cap.low
                if (l1 == 3) {
                    int cap = N[i].s_1[0] - 'A', low = N[i].s_1[2] - 'a';
                    for (auto it_1 : SS[tem_1].S) {
                        for (auto it_2 : SS[tem_2].S) {
                            amore[it_1 - 'a'][low].insert(it_2);
                        }
                    }
                } else {
                    int cap = N[i].s_2[0] - 'A', low = N[i].s_2[2] - 'a';
                    for (auto it_1 : SS[tem_2].S) {
                        for (auto it_2 : amore[it_1 - 'a'][low]) {
                            SS[tem_1].S.insert(it_2);
                        }
                    }
                }
            }  
        }
 
    }
     
    for (int i = 0; i < 26; i++) {
        printf("%c: ", char(i + 'A'));
        for (auto it : SS[i].S) cout << it;
        puts("");
    }
}
 
int main()
{
 
//    freopen("F:/Overflow/in.txt","r",stdin);
//    ios::sync_with_stdio(false);
    solve();
    return 0;
}

/*************************************************************************
 > FileName:
 > Author:      Lance
 > Mail:        lancelot_hcs@qq.com
 > Date:        9102.1.8
 > Description:
 ************************************************************************/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const double pi = acos(-1.0);
const double eps = 1e-6;
const int mod = 1e9 + 7;
#define debug(a) cout << "*" << a << "*" << endl
const int INF = 0x3f3f3f3f;//int2147483647//ll9e18//unsigned ll 1e19
const int maxn = 250;
const int M = 26 + 26 * 26;
//sacnf("%lf") printf("%f")
ll read()
{
    ll x = 0,f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
        f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
int t, n;
struct node {
    string s_1, equal, s_2;
}N[maxn];
 
int f[M];
 
inline bool check_low(char c) {
    return c >= 'a' && c <= 'z';
}
 
inline int turn(char c) {
    if (check_low(c)) return c - 'a';
    else if(c >= 'A' && c <= 'Z') return c - 'A';
}
int con1 = 0, con2 = 0, con3 = 0, con4 = 0;
void solve()
{
    n = read();
    for (int i = 0; i < n; i++) cin >> N[i].s_1 >> N[i].equal >> N[i].s_2;
     
    for (int i = 0; i < 26 * M; i++) {
        for (int j = 0; j < n; j++) {
            int l1 = N[j].s_1.size(), l2 = N[j].s_2.size();
            if (islower(N[j].s_2[0])) f[N[j].s_1[0]-'A'] |= 1 << (N[j].s_2[0] -'a'),con1++;
            else if (l1 == 1 && l2 == 1) f[N[j].s_1[0] - 'A'] |= f[N[j].s_2[0] -'A'], con2++;
            else if (l1 > l2)
                for (int k = 0; k < 26; k++) {
                    if (f[N[j].s_1[0] - 'A'] >> k & 1)
                        f[26 + k * 26 + N[j].s_1[2] - 'a'] |= f[N[j].s_2[0] - 'A'], con3++;
                }
                         
            else
                for (int k = 0; k < 26; k++)
                    if (f[N[j].s_2[0] - 'A']>>k&1)
                        f[N[j].s_1[0] - 'A'] |= f[26 + k * 26 + N[j].s_2[2] -'a'];         
        }
    }
    for (int i = 0; i < 26; i++) {
        printf("%c: ", char(i + 'A'));
        for (int j = 0; j < 26; j++) if (f[i] >> j & 1) printf("%c", char('a' + j));
        puts("");
    }
}
 
int main()
{
 
//    freopen("F:/Overflow/in.txt","r",stdin);
//    ios::sync_with_stdio(false);
    solve();
    return 0;
}

参考博客

https://blog.nowcoder.net/n/128cf2deb7a54cbaa825427092e84ebc

https://blog.csdn.net/qq_43765333/article/details/107747083

posted @ 2020-08-02 18:17 Lancelot& 阅读(228) 评论(0) 收藏举报

刷新页面返回顶部

动无常则若危若安

2020牛客暑期多校训练营（第七场）补题

B. Mask Allocation

题意

思路

代码

H. Dividing

题意

思路

代码

J. Pointer Analysis

题意

思路

代码

参考博客

公告

动无常则 若危若安

2020牛客暑期多校训练营（第七场）补题

B. Mask Allocation

题意

思路

代码

H. Dividing

题意

思路

代码

J. Pointer Analysis

题意

思路

代码

参考博客

公告

动无常则若危若安