Unity 凹多边形三角剖分

游戏中需要实现一个小功能，显示一个玩家的能力图，这个图是一个有6个顶点任意摆放组合的多边形。而绘制多边形主要用到的知识就是Mesh构建，mesh的构建主要需要顶点列表，三角形列表，法线列表、uv列表等等等等，在这里我们只考虑顶点列表和三角形列表。那么我们需要做的就是给定一组顶点之后，如何用三角形进行划分，以便绘制。

以下讨论的多边形：1.三角形顶点列表为顺时针顺序。2.多边形不能包含空洞。

参照文章：https://blog.csdn.net/huangzengman/article/details/77114082，表示感谢

 

1.凸多边形

凸多边形三角剖分比较简单，可以使用第一个点依次连接后面的其他点来组成一组共同顶点的三角形。当然这是最简单的凸多边形剖分算法，还有其他最优剖分算法，需要考虑权重等，但我们不需要。

   

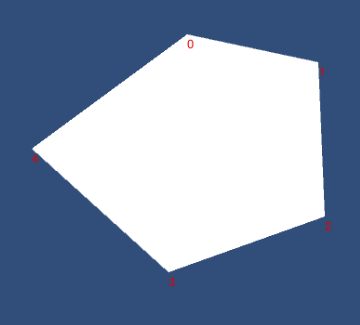
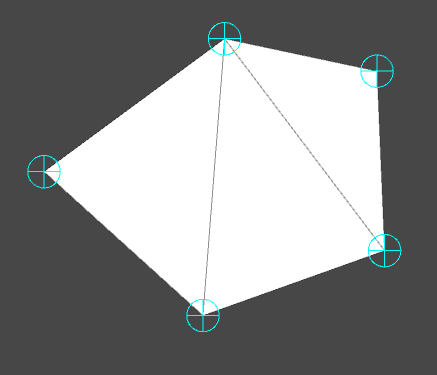
                                            a                                                                                                     b

图a为凸多边形，标出了顶点序号。

图b为三角剖分后，unity中所显示的三角形网格。

 

2.凹多边形

凹多边形的剖分则需要判断点与多边形的关系，以此来确定可划分顶点与不可划分顶点。

 

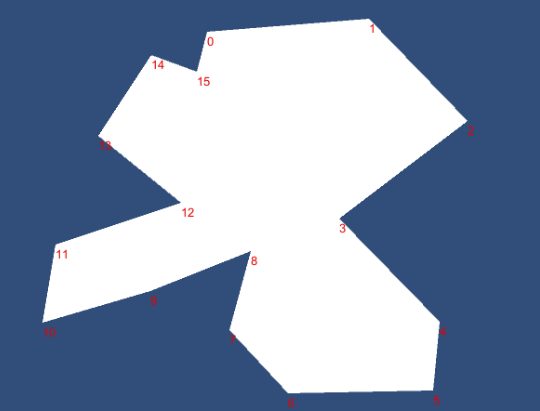
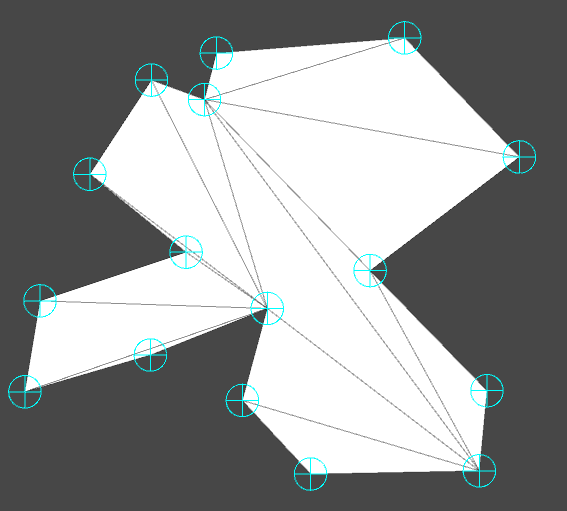
                                                             a                                                                                                                                                b

图a为凹多边形（没有空洞），标出了顶点序号。

图b为三角剖分后，unity中所显示的三角形网格。

代码如下，参考上述连接：

1.MeshDrawBase.cs           基础类

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public abstract class MeshDrawBase : MonoBehaviour {

    protected MeshFilter targetFilter;
    protected Mesh mesh;
    protected int[] tris;
    protected Vector2[] uvs;
    protected Vector3[] normals;

    // Use this for initialization
    void Awake () {
        targetFilter = GetComponent<MeshFilter>();
    }
    
    // Update is called once per frame
    protected virtual void Update () {
        DrawMesh();
    }

    protected abstract void DrawMesh();
}

2.Polygon.cs                       用于绘制多边形

using System.Collections.Generic;
using UnityEngine;

public class Polygon : MeshDrawBase
{
    public List<Vector3> points = new List<Vector3>();
    public List<int> indexes = new List<int>();
    int index = 0;
    Color[] colors;

    void Start()
    {
        /*points.Add(new Vector3(0, 0, 0));
        points.Add(new Vector3(0, 1, 0));
        points.Add(new Vector3(1, 1, 0));
        points.Add(new Vector3(0.7f, 0.8f, 0));
        points.Add(new Vector3(1, 0.5f, 0));
        points.Add(new Vector3(0.7f, 0.3f, 0));
        points.Add(new Vector3(1, 0, 0));
        indexes.Add(0);
        indexes.Add(1);
        indexes.Add(2);
        indexes.Add(3);
        indexes.Add(4);
        indexes.Add(5);
        indexes.Add(6);*/
    }

    protected override void DrawMesh()
    {
        if(Input.GetKeyDown(KeyCode.D))
        {
            DrawPolygon();
        }
    }

    private void DrawPolygon()
    {
        mesh = new Mesh();
        mesh.name = "Polygon";
        mesh.vertices = points.ToArray();
        
        tris = Triangulation.WidelyTriangleIndex(new List<Vector3>(points), indexes).ToArray();

        mesh.triangles = tris;

        normals = new Vector3[mesh.vertices.Length];
        for(int i = 0; i < mesh.vertices.Length; ++i)
        {
            normals[i] = new Vector3(0, 0, 1);
        }

        mesh.normals = normals;
        
        mesh.RecalculateBounds();
        mesh.RecalculateTangents();

        targetFilter.mesh = mesh;
    }

    protected override void Update()
    {
        base.Update();
        if(Input.GetMouseButtonDown(0))
        {
            Ray ray = Camera.main.ScreenPointToRay(Input.mousePosition);
            RaycastHit hit;
            if(Physics.Raycast(ray, out hit, Mathf.Infinity))
            {
                var worldHitPos = hit.point;
                var localHitPos = transform.InverseTransformPoint(worldHitPos);

                points.Add(localHitPos);
                indexes.Add(index++);
            }
        }

        if(Input.GetKeyDown(KeyCode.R))
        {
            this.Reset();
        }
    }

    private void Reset()
    {
        points.Clear();

        targetFilter.mesh = null;
        Destroy(mesh);
    }

    private void OnGUI()
    {
        if (points.Count == 0) return;

        GUI.color = Color.red;

        for(int i = 0; i < points.Count; ++i)
        {
            var worldPos = transform.TransformPoint(points[i]);
            var screenPos = Camera.main.WorldToScreenPoint(worldPos);
            var uiPos = new Vector3(screenPos.x, Camera.main.pixelHeight - screenPos.y, screenPos.z);

            GUI.Label(new Rect(uiPos, new Vector2(100, 80)), i.ToString());
        }
    }

    private void OnDrawGizmos()
    {
        if (points.Count == 0) return;

        Gizmos.color = Color.cyan;
        foreach(var pos in points)
        {
            var worldPos = transform.TransformPoint(pos);
            Gizmos.DrawWireSphere(worldPos, .2f);
        }
    }
}

3.Triangulation.cs               三角剖分工具类

using UnityEngine;
using System.Collections.Generic;

/// <summary>
/// 三维模型重建中的凹多边形三角剖分，适用于不带空洞的凹多边形
/// ref: https://blog.csdn.net/huangzengman/article/details/77114082
/// </summary>
public static class Triangulation
{
    const double epsilon = 1e-7;

    static bool floatLess(float value, float other)
    {
        return (other - value) > epsilon;
    }

    static bool floatGreat(float value, float other)
    {
        return (value - other) > epsilon;
    }

    static bool floatEqual(float value, float other)
    {
        return Mathf.Abs(value - other) < epsilon;
    }

    static bool Vector3Equal(Vector3 a, Vector3 b)
    {
        return floatEqual(a.x, b.x) && floatEqual(a.y, b.y) && floatEqual(a.z, b.z);
    }

    /// <summary>
    /// 凸多边形，顺时针序列，以第1个点来剖分三角形，如下：
    /// 0---1
    /// |   |
    /// 3---2  -->  (0, 1, 2)、(0, 2, 3)
    /// </summary>
    /// <param name="verts">顺时针排列的顶点列表</param>
    /// <param name="indexes">顶点索引列表</param>
    /// <returns>三角形列表</returns>
    public static List<int> ConvexTriangleIndex(List<Vector3> verts, List<int> indexes)
    {
        int len = verts.Count;
        //若是闭环去除最后一点
        if (len > 1 && Vector3Equal(verts[0], verts[len - 1]))
        {
            len--;
        }
        int triangleNum = len - 2;
        List<int> triangles = new List<int>(triangleNum * 3);
        for (int i = 0; i < triangleNum; i++)
        {
            triangles.Add(indexes[0]);
            triangles.Add(indexes[i + 1]);
            triangles.Add(indexes[i + 2]);
        }
        return triangles;
    }

    /// <summary>
    /// 三角剖分
    /// 1.寻找一个可划分顶点
    /// 2.分割出新的多边形和三角形
    /// 3.新多边形若为凸多边形，结束；否则继续剖分
    /// 
    /// 寻找可划分顶点
    /// 1.顶点是否为凸顶点：顶点在剩余顶点组成的图形外
    /// 2.新的多边形没有顶点在分割的三角形内
    /// </summary>
    /// <param name="verts">顺时针排列的顶点列表</param>
    /// <param name="indexes">顶点索引列表</param>
    /// <returns>三角形列表</returns>
    public static List<int> WidelyTriangleIndex(List<Vector3> verts, List<int> indexes)
    {
        int len = verts.Count;
        if (len <= 3) return ConvexTriangleIndex(verts, indexes);

        int searchIndex = 0;
        List<int> covexIndex = new List<int>();
        bool isCovexPolygon = true;//判断多边形是否是凸多边形

        for (searchIndex = 0; searchIndex < len; searchIndex++)
        {
            List<Vector3> polygon = new List<Vector3>(verts.ToArray());
            polygon.RemoveAt(searchIndex);
            if (IsPointInsidePolygon(verts[searchIndex], polygon))
            {
                isCovexPolygon = false;
                break;
            }
            else
            {
                covexIndex.Add(searchIndex);
            }
        }

        if (isCovexPolygon) return ConvexTriangleIndex(verts, indexes);

        //查找可划分顶点
        int canFragementIndex = -1;//可划分顶点索引
        for (int i = 0; i < len; i++)
        {
            if (i > searchIndex)
            {
                List<Vector3> polygon = new List<Vector3>(verts.ToArray());
                polygon.RemoveAt(i);
                if (!IsPointInsidePolygon(verts[i], polygon) && IsFragementIndex(i, verts))
                {
                    canFragementIndex = i;
                    break;
                }
            }
            else
            {
                if (covexIndex.IndexOf(i) != -1 && IsFragementIndex(i, verts))
                {
                    canFragementIndex = i;
                    break;
                }
            }
        }

        if (canFragementIndex < 0)
        {
            Debug.LogError("数据有误找不到可划分顶点");
            return new List<int>();
        }

        //用可划分顶点将凹多边形划分为一个三角形和一个多边形
        List<int> tTriangles = new List<int>();
        int next = (canFragementIndex == len - 1) ? 0 : canFragementIndex + 1;
        int prev = (canFragementIndex == 0) ? len - 1 : canFragementIndex - 1;
        tTriangles.Add(indexes[prev]);
        tTriangles.Add(indexes[canFragementIndex]);
        tTriangles.Add(indexes[next]);
        //剔除可划分顶点及索引
        verts.RemoveAt(canFragementIndex);
        indexes.RemoveAt(canFragementIndex);

        //递归划分
        List<int> leaveTriangles = WidelyTriangleIndex(verts, indexes);
        tTriangles.AddRange(leaveTriangles);

        return tTriangles;
    }

    /// <summary>
    /// 是否是可划分顶点:新的多边形没有顶点在分割的三角形内
    /// </summary>
    private static bool IsFragementIndex(int index, List<Vector3> verts)
    {
        int len = verts.Count;
        List<Vector3> triangleVert = new List<Vector3>();
        int next = (index == len - 1) ? 0 : index + 1;
        int prev = (index == 0) ? len - 1 : index - 1;
        triangleVert.Add(verts[prev]);
        triangleVert.Add(verts[index]);
        triangleVert.Add(verts[next]);
        for (int i = 0; i < len; i++)
        {
            if (i != index && i != prev && i != next)
            {
                if (IsPointInsidePolygon(verts[i], triangleVert))
                {
                    return false;
                }
            }
        }
        return true;
    }

    /// <summary>
    /// 射线与线段相交性判断
    /// </summary>
    /// <param name="ray">射线</param>
    /// <param name="p1">线段头</param>
    /// <param name="p2">线段尾</param>
    /// <returns></returns>
    private static bool IsDetectIntersect(Ray2D ray, Vector3 p1, Vector3 p2)
    {
        float pointY;//交点Y坐标，x固定值
        if (floatEqual(p1.x, p2.x))
        {
            return false;
        }
        else if(floatEqual(p1.y, p2.y))
        {
            pointY = p1.y;
        }
        else
        {
            //直线两点式方程：(y-y2)/(y1-y2) = (x-x2)/(x1-x2)
            float a = p1.x - p2.x;
            float b = p1.y - p2.y;
            float c = p2.y / b - p2.x / a;

            pointY = b / a * ray.origin.x + b * c;
        }
        
        if (floatLess(pointY, ray.origin.y))
        {
            //交点y小于射线起点y
            return false;
        }
        else
        {
            Vector3 leftP = floatLess(p1.x, p2.x) ? p1 : p2;//左端点
            Vector3 rightP = floatLess(p1.x, p2.x) ? p2 : p1;//右端点
            //交点x位于线段两个端点x之外，相交与线段某个端点时，仅将射线L与左侧多边形一边的端点记为焦点(即就是：只将右端点记为交点)
            if (!floatGreat(ray.origin.x, leftP.x) || floatGreat(ray.origin.x, rightP.x))
            {
                return false;
            }
        }

        return true;
    }

    /// <summary>
    /// 点与多边形的位置关系
    /// </summary>
    /// <param name="point">判定点</param>
    /// <param name="polygonVerts">剩余顶点按顺序排列的多边形</param>
    /// <returns>true:点在多边形之内，false:相反</returns>
    private static bool IsPointInsidePolygon(Vector3 point, List<Vector3> polygonVerts)
    {
        int len = polygonVerts.Count;
        Ray2D ray = new Ray2D(point, new Vector3(0, 1)); //y方向射线
        int interNum = 0;

        for (int i = 1; i < len; i++)
        {
            if (IsDetectIntersect(ray, polygonVerts[i - 1], polygonVerts[i]))
            {
                interNum++;
            }
        }

        //不是闭环
        if (!Vector3Equal(polygonVerts[0], polygonVerts[len - 1]))
        {
            if (IsDetectIntersect(ray, polygonVerts[len - 1], polygonVerts[0]))
            {
                interNum++;
            }
        }
        int remainder = interNum % 2;
        return remainder == 1;
    }
}

使用方法：新建一个Quad，将Polygon.cs脚本添加上，用鼠标点击来确定多边形的个顶点位置，之后按D进行绘制。

git：https://gitee.com/planefight/RunSprite_Tri.git

 

 

参照论文：

三维模型重建中的凹多边形三角剖分：