MIT Linear algebra notes
第十五节课 投影
投影矩阵P = A * A^T / (A^T * A) （PS：一维情况下）
投影矩阵的列空间是通过向量A的一条直线
投影矩阵的秩为1
投影矩阵是对称矩阵
投影矩阵的平方仍然是投影矩阵，即 P^2 = P ,做一次投影后，在做一次投影，得到的位置仍然是第一次投影的位置
投影矩阵P = A * (（A^T * A）^(-1) ) * A^T (PS: 多维情况写）
-------------------------------------------------------------
第十四节课 正交向量和正交子空间
首先介绍了正交的概念
矩阵的行空间和零空间正交，因为Ax = 0，将矩阵拆为每一行，相乘等于0，行空间中除了矩阵中的行，还有矩阵中每一行的线性组合，但每一行相乘都为0 ，故正交
A^T * A 的到的是方阵且是对称阵
当处理的数据（矩阵A的形式体现）中含有一些脏数据且不知道哪些数据是脏数据时，可以将方程Ax = 0转化为A^T * A * x = A^T * B
-------------------------------------------------------------
第十三节课 复习一
矩阵的平方等于0，不能推出矩阵为0矩阵
如果矩阵A，B含有相同的4个子空间，那么A = cB，是错误的
矩阵交换了其中的两行，矩阵的行空间和零空间不变
--------------------------------------------------------------
第十二节课 图和网络
图包含节点和边
根据图写出矩阵形式，联系到KCL定律。惊了
没有回路的图，表示线性无关
没有回路的图称作树
介绍了图上的欧拉公式
--------------------------------------------------------------
第十一节课 矩阵空间、秩1矩阵和小世界图
-----------------------------------------------------------------
第十节课 四个基本子空间
四个基本子空间是列子空间、零子空间、行子空间、A转置的零子空间
矩阵A是m * n的矩阵
行子空间和A转置的零子空间为A矩阵转制后的子空间，计算方法和原来有些类似
（A， I） --> (R, E)
E * A = R
对矩阵A做化简为R（行最简）的线性变换，右边的增广矩阵I其实是相当于记录了变换方法
最后将向量空间扩展到矩阵空间，矩阵和矩阵之间的运算也可以满足空间的定义
举例三种矩阵，上三角矩阵、对称矩阵、对角线矩阵
以对角线矩阵为例，两个对角线矩阵进行加和数乘操作后所得到的新矩阵仍是对角线矩阵
------------------------------------------------------------------
第九节课 线性相关性、基、维数
线性相关，Ax = 0有非全零解
线性无关，向量组合不为0
基是一组线性无关的向量，并生成空间
维数指基向量的个数
矩阵A的秩r = 矩阵中主列的个数 = 矩阵A列空间的维数
零空间的维数 = 矩阵中自由变量的个数 = n - r
-------------------------------------------------------------------------
第八节课 可解性及解的结构
Ax = B的解为特解+零向量解
A矩阵为n列，m行，r为矩阵的秩，R为行最简矩阵
当r = n = m时，R = I，行最简矩阵等于单位矩阵，此时存在1解
当r = n < m时，
，此时方程存在1解或0解
当r = m < n时，R = （I， F）（PS：F的列可以和I的列相间出现），此时存在无穷解
当r < n, r < m时，
，此时无解或无穷解
矩阵的秩决定了方程组解的数目
------------------------------------------------------------------
第七节课 主变量、特解
主列指的是主元所在的列，其他列称为自由列
矩阵A先将下方都化为0变为矩阵U
关于AX = 0，求出X的解
定义主列的矩阵为F，化简后右侧的矩阵为I，
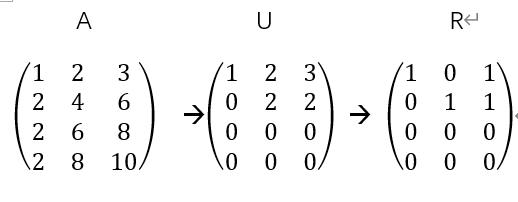
其中矩阵R右上角的列向量（1，1）记作F
X的解为
----------------------------------------------------------------------------
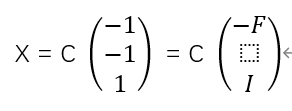
第六节课 列空间和零空间
两个向量子空间的交集仍是向量子空间
向量子空间一定包括零向量
感觉没学到什么新的东西，大一学过了
----------------------------------------------------------------------------
第五节课 转置、置换、向量空间
PA = LU 置换矩阵是行重新排列的单位矩阵
n阶矩阵的置换矩阵有n！个，置换矩阵的逆矩阵等于矩阵的转置
矩阵的转置 * 矩阵 = 对称矩阵
(R' * R)' = R' * R'' = R' * R
R^2的子空间三种情况
1.R^2空间为自己的子空间
2.经过原点的直线
3.原点
--------------------------------------------------------------------------------
第四节课 A的LU分解
这节课画质有点渣
A^(-1) * A = I，A * B * B^(-1) * A^(-1) = I
E21的求法在第1节还是第二节的课上讲过，U矩阵是A矩阵的第二行减去4倍的第一行，所以E21矩阵这样得出
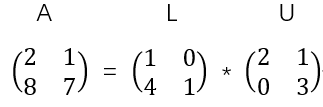
L其实为矩阵E21的逆矩阵，这个逆矩阵的求法是利用了E21的求法，所以逆操作是第一行4倍加上第二行，具体的可以看这里，（L是下三角的缩写，U是上三角的缩写）
关于高斯消元复杂度N3的证明，每变一个数需要操作n次，一列有n数，一共有n列，所以n3
-----------------------------------------------------------------------
第三节课 矩阵乘法和逆
矩阵乘法
矩阵相乘的四种做法n*m的矩阵A乘以m*p的矩阵B最后得到n*p的矩阵C
第一种做法，矩阵C中每个位置的值由两个向量的点积得到
第二种做法，矩阵A乘以矩阵B中的第一列得到矩阵C中的第一列，矩阵A乘以矩阵B的第二列得到矩阵C的第二列，以此类推
第三种做法，矩阵A的第一行乘以矩阵B得到矩阵C的第一行，以此类推
第四种做法，矩阵C等于矩阵A的每一列乘以矩阵B的每一行，然后将所得的每一个矩阵在进行相加
关于分块矩阵的做法，和矩阵同理
矩阵的逆
A^(-1) * A = I
方阵的左逆和右逆是相同的，若矩阵不为方阵则左逆和右逆不同
行列式的值不为0 ，矩阵可逆
上述矩阵所表示的向量在同一直线上，怎么组合都不能组合出单位矩阵的向量，所以上述矩阵没有逆
另上述矩阵为A，存在列向量B（3，-1）使得A*B = 0。等号两边左侧乘以A^(-1)，得到B = 0，但B≠0，所以矩阵A的逆不存在
矩阵求逆的方法，
构造（A | I）的一个矩阵，通过行变换，将矩阵的左侧变换为单位矩阵I，则矩阵右侧的部分就是矩阵A的逆矩阵
证明：矩阵的变换可以看做矩阵左侧乘以一个新的变换矩阵E，E * (A | I) ----> (E * A | E * I ) ----> ( I | E)，由于A^(-1) * A = I，所以右侧为矩阵的逆
-------------------------------------------------------------------------------------
第二节课 矩阵消元
演示了方程组的解法，先提取矩阵系数，然后将矩阵化为上三角矩阵，求解出答案后再回带到所有方程，最终得出方程的解。
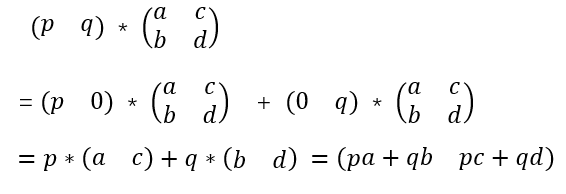
一个一维横向量左乘一个矩阵，可以将矩阵拆分为多个横向量乘以对应倍数相加。
如果矩阵右乘一个（竖）向量，以（1，0，0）为例，表示保留矩阵第一列，乘以1倍的系数，
因此单位矩阵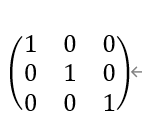
乘以一个矩阵仍等于原矩阵
最后引入了矩阵的逆，矩阵A乘以矩阵A的逆 = I（单位矩阵）
----------------------------------------------------------------------------------
第一节课 方程组的几何解释
主要讲解了方程组的横向和纵向画法，以二元方程组为例
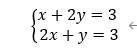
横向的画法是在二维平面图中做出每个方程所对应的直线方程，若方程组为x维方程，在x维中坐标系下，每一个方程表示x维坐标系下的x - 1维的空间，若上述方程组存在解，所有x - 1维空间相交于一点，此点的坐标就是方程组的解
纵向画法是将方程组先改写为矩阵形式
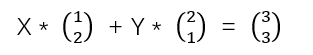
将其中的每一个向量在空间坐标系中划出，可以容易得到向量（3，3）由1个向量（1，2）和1个向量（2，1）相加，这是纵向画法的意义
----------------------------------------------------------------
2个月没有更新了，在家看了一些书，学习了一些常见的经济学的原理。
