IOI 2026 中国国家集训队作业(试题泛做)个人题解
QOJ 4802 Ternary Search
题意
给你一个长度为 \(n\) 的序列 \(a\),对每一个前缀查询:
- 任意交换相邻两项,把序列变成单峰或单谷的最小操作次数。
\(n \le 2 \times 10 ^ 5, a_i \le 10 ^ 9\)。
思路
单峰和单谷可以互相转换,方法是 \(\forall i \in [1, n], a_i \leftarrow n + 1 - a_i\)。
把单峰转换为单谷。
Part 1
看到求解邻项交换次数最小值的问题,应该想到转换为求解逆序对个数最小值。
但是很不好,这是单谷序列而不是单调序列。
对于一个单谷的序列:
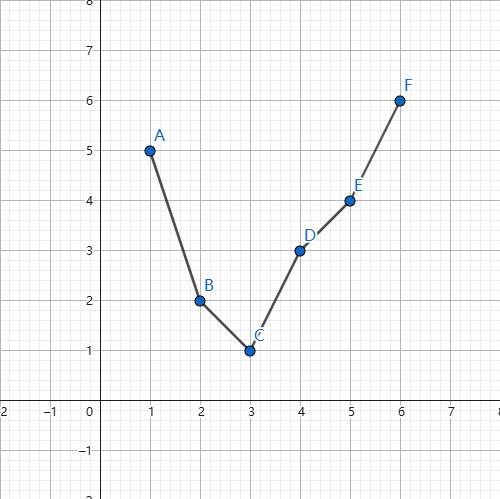
我们想要把前半部分转换一下,使得整个序列变成单调的,不难想到对一个前缀取相反数。
所以我们现在这样描述单谷序列:
- 可以将一个前缀取相反数后得到递增序列。
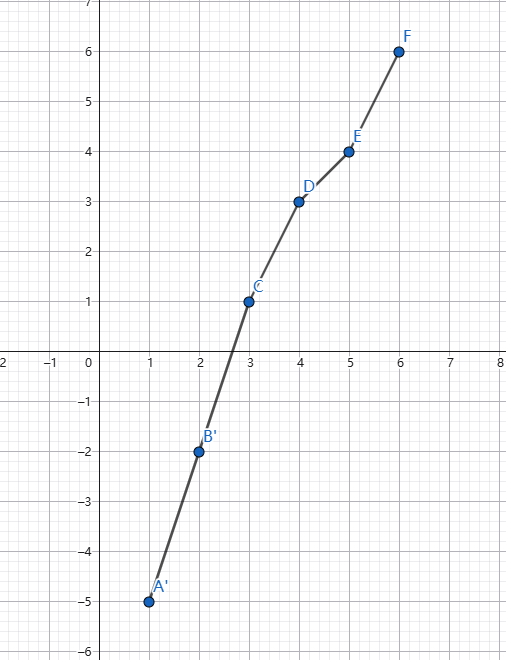
Part 2
我们现在的问题是在 \(a\) 的一个前缀里选择一些数取相反数,求逆序对个数的最小值。
因为逆序对研究数的相对大小,那么我们考虑最大值 \(mx\) 这个特殊的元素。
可以发现,最大值在取反后是严格的最小值,这意味着他只能和一侧的数构成逆序对,并且与剩下数是否取反无关,也就可以方便地计算逆序对。
具体地,对于最大值:
- 如果不取反,逆序对个数是在 \(mx\) 右边的数个数
- 如果取反,逆序对个数是在 \(-mx\) 左边的数的个数。
然后我们可以把 \(mx\) 删掉不考虑,然后得到一个有新的 \(mx'\) 的子问题。
推广上述结论,对于一个数 \(x\):
- 如果不取反,逆序对个数就是「在 \(x\) 左边的数中,比 \(x\) 晚被删去」的数的个数。
也就是「\(x\) 左边小于 \(x\) 的数个数」。 - 如果取反,就是「\(x\) 右边小于 \(x\) 的数个数」。
Part 3
接下来我们考虑新加入一个数的时候,答案的改变情况。
记 \(wl_i\) 为「\(a_i\) 左边小于 \(a_i\) 的数个数」,\(wr_i\) 为「\(a_i\) 右边小于 \(a_i\) 的数个数」。
可以发现 \(wl_i\) 在 \(a_i\) 加入的时候就已经确定了。
而随着更多的数加入,\(wr_i\) 逐渐增加,直到某一时刻超过 \(wl_i\)。
所以 \(\min(wl_i, wr_i)\) 会在某一时刻前取 \(wr_i\),该时刻后取 \(wl_i\)。
而我们需要支持加入 \(a_i\) 时给 \(\forall j, a_j \gt a_i\) 的 \(wr_j\) 更新,且需要支持单点修改。
考虑权值线段树维护。
对于这种「每个元素都有一个不同的阈值」类型问题(瞎起的名字),可以维护 \(d_i = wl_i - wr_i\),表示距离阈值的差距。(在所有时刻,保证 \(d_i \ge 0\)。)
每一次的更改就变成了给权值线段树上 \((a_i, n]\) 的区间 \(d\) 自减(\(d = 0\) 除外)。
每一个前缀的答案就是 \(\sum \min(wl_i, wr_i) = \left( \sum_i wl_i \right) - \left( \sum_i d_i \right)\)。
线段树需要维护 \(\sum d\),而且我们每次区间修改 \(d \leftarrow d - 1\) 时需要忽略 \(d = 0\) 的,
所以需要维护 \(cnt\) 表示区间内 \(d \not = 0\) 的个数,同时需要在区间修改后清空 \(d = 0\) 对应的 \(cnt\)。
此处暴力清空即可,每个下标只会被清空一次,清空总时间复杂度 \(\mathcal{O}(n \log n)\)。
另外在给 \(d\) 赋初始值 \(wl\) 时需要树状数组维护一下。
总时间复杂度 \(\mathcal{O}(n \log n)\)。
代码
const int N = 2e5 + 5;
const ll inf = 0x3f3f3f3f3f3f3f3f;
int n;
int a[N];
int v[N], vn;
ll ans[N];
struct BIT{
int c[N];
void init(){
rep(i, 1, n) c[i] = 0;
}
int lowbit(int x){
return x & -x;
}
void add(int i, int v){
for(; i <= n; i += lowbit(i)){
c[i] += v;
}
}
int query(int i){
int res = 0;
for(; i; i -= lowbit(i)){
res += c[i];
}
return res;
}
} BIT;
struct SMT{
struct node{
ll sum;
int mn, tag, cnt;
// sum_d, mn_d, add_tag, count_of_d_=_0
} t[N << 2];
#define ls(x) (x << 1)
#define rs(x) ((x << 1) | 1)
#define mid ((l + r) >> 1)
void push_up(int x){
t[x].sum = t[ls(x)].sum + t[rs(x)].sum;
t[x].cnt = t[ls(x)].cnt + t[rs(x)].cnt;
t[x].mn = inf;
if(t[ls(x)].cnt) t[x].mn = min(t[x].mn, t[ls(x)].mn);
if(t[rs(x)].cnt) t[x].mn = min(t[x].mn, t[rs(x)].mn);
}
void hard(int x, int v){
t[x].tag += v;
t[x].sum += t[x].cnt * v;
if(t[x].cnt) t[x].mn += v;
}
void push_down(int x){
if(t[x].tag){
hard(ls(x), t[x].tag);
hard(rs(x), t[x].tag);
t[x].tag = 0;
}
}
void build(int x, int l, int r){
if(l == r){
t[x].mn = inf;
t[x].sum = t[x].cnt = 0;
t[x].tag = 0;
return;
}
build(ls(x), l, mid);
build(rs(x), mid + 1, r);
push_up(x);
}
void modify_point(int x, int l, int r, int p, int v){
if(l == r){
t[x].sum = t[x].mn = v;
t[x].cnt = (v != 0);
return;
}
push_down(x);
if(p <= mid) modify_point(ls(x), l, mid, p, v);
else modify_point(rs(x), mid + 1, r, p, v);
push_up(x);
}
void add_range(int x, int l, int r, int ql, int qr, int v){
if(ql > qr) return;
if(t[x].cnt == 0) return;
if(ql <= l && r <= qr){
hard(x, v);
return;
}
push_down(x);
if(ql <= mid) add_range(ls(x), l, mid, ql, qr, v);
if(qr > mid) add_range(rs(x), mid + 1, r, ql, qr, v);
push_up(x);
}
void update(int x, int l, int r, int ql, int qr){
if(ql > qr) return;
if(t[x].mn) return;
if(l == r){
t[x].cnt = 0;
return;
}
push_down(x);
if(ql <= mid) update(ls(x), l, mid, ql, qr);
if(qr > mid) update(rs(x), mid + 1, r, ql, qr);
push_up(x);
}
#undef ls
#undef rs
#undef mid
} SMT;
void solve(){
BIT.init();
SMT.build(1, 1, n);
ll sum_l = 0;
rep(i, 1, n){
int cnt_l = BIT.query(a[i]);
sum_l += cnt_l;
BIT.add(a[i], 1);
SMT.modify_point(1, 1, n, a[i], cnt_l);
SMT.add_range(1, 1, n, a[i] + 1, n, -1);
SMT.update(1, 1, n, a[i] + 1, n);
ans[i] = min(ans[i], sum_l - SMT.t[1].sum);
}
}
void solve_test_case(){
n = read();
rep(i, 1, n){
a[i] = read();
v[i] = a[i];
ans[i] = inf;
}
sort(v + 1, v + n + 1);
vn = unique(v + 1, v + n + 1) - v - 1;
rep(i, 1, n){
a[i] = lower_bound(v + 1, v + vn + 1, a[i]) - v;
}
solve();
rep(i, 1, n) a[i] = vn + 1 - a[i];
solve();
rep(i, 1, n){
write(ans[i]);
}
}
QOJ 4788 Gravity
题意
给你一个 \(n \times n\) 的网格图,每个格子有障碍('#')或者没有('.'),一个极大的障碍的四联通块算一个物品,所有物品按照重力往下掉,要求输出最后的结果。
\(n \le 2000\)。
思路
先 bfs 把所有的连通块搜出来。
..........
..######..
..#....#..
..#.#..#..
..#..#.#..
..#....#..
..######..
..........
..#....#..
.......#..
然后按照竖列考虑,对于一个竖列上下相邻的两个物品,上面的物品最多只能下落到下面物品的位置。
令 \(h_i\) 表示第 \(i\) 个物品的下落高度,\(id_{(x, y)}\) 为 \((x, y)\) 这个障碍所在的物品编号。(\(x\) 是行编号,\(y\) 是列编号)
对于 \((x_1, y), (x_2, y), x_1 \lt x_2, \not \exists x_1 \lt x_3, \lt x_2, (x_3, y) 是障碍\) 则称 \((x_1, y), (x_2, y)\) 同列相邻。
则对于所有同列相邻的 \((x_1, y), (x_2, y), h_{id_{(x_1, y)}} \le h_{id_{(x_2, y)}} + (x_2 - x_1 - 1)\)。
差分约束系统,将 \(id_{(x_1, y)}\) 和 \(id_{(x_2, y)}\) 连边。这里方便考虑,把整个 \(n + 1\) 行当作一个物品。
代码
char read_ch(){
char c = getchar();
for(; c != '#' && c != '.'; ) c = getchar();
return c;
}
const int N = 2005;
int n, m;
bool mp[N][N], mp2[N][N];
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, 1, -1};
int bid[N][N], bcnt;
void bfs(int sx, int sy, int cur_id){
queue<pair<int, int>> q;
q.push({sx, sy});
bid[sx][sy] = cur_id;
while(!q.empty()){
int x = q.front().first, y = q.front().second;
q.pop();
rep(d, 0, 3){
int nx = x + dx[d];
int ny = y + dy[d];
if(!bid[nx][ny] && 1 <= nx && nx <= n && 1 <= ny && ny <= m && mp[nx][ny]){
bid[nx][ny] = cur_id;
q.push({nx, ny});
}
}
}
}
int calc(int x, int y){
return (x - 1) * n + y;
}
pair<int, int> rev_calc(int id){
int y = id % n, x = id / n + 1;
return make_pair(x, y);
}
struct edge{
int v, w;
};
vector<edge> e[N * N];
int dis[N * N];
bool vis[N * N];
void dijkstra(){
memset(dis, 0x3f, sizeof(dis));
dis[bcnt] = 0;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
q.push({dis[bcnt], bcnt});
while(!q.empty()){
int u = q.top().second; q.pop();
if(vis[u]) continue;
vis[u] = 1;
for(edge E : e[u]){
int v = E.v, w = E.w;
if(vis[v]) continue;
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
q.push({dis[v], v});
}
}
}
}
signed main(){
n = read(), m = read();
rep(i, 1, n){
rep(j, 1, m){
mp[i][j] = (read_ch() == '#');
}
}
rep(i, 1, n){
rep(j, 1, m){
if(mp[i][j] && !bid[i][j]){
bfs(i, j, ++bcnt);
}
}
}
bcnt++;
rep(j, 1, m){
bid[n + 1][j] = bcnt;
}
rep(x, 1, n + 1){
rep(y, 1, m){
int up = x - 1;
while(up && !mp[up][y]) up--;
if(bid[up][y] == bid[x][y] || mp[up][y] == 0) continue;
e[bid[x][y]].push_back({bid[up][y], x - up - 1});
}
}
dijkstra();
rep(i, 1, n){
rep(j, 1, m){
if(mp[i][j]){
mp2[i + dis[bid[i][j]]][j] = 1;
}
}
}
rep(i, 1, n){
rep(j, 1, m){
if(mp2[i][j]){
putchar('#');
}else{
putchar('.');
}
}
puts("");
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号