瞎说虚树
概述
虚树是针对一种特定的树上问题的做法。
虚树研究的问题中一般有 \(k\) 个特殊点,除此之外的点一般可以方便地合并考虑。
一个很经典的(也可能是主要的)用途是用来研究关键点之间的路径问题。
定义
虚树需要满足以下性质:
-
保留原树的祖先后代结构,对于均在虚树上出现的 \(u, v\),「虚树上 \(u\) 是 \(v\) 的祖先」是「原树上 \(u\) 是 \(v\) 的祖先」的充要条件。
这个结论可以推出虚树上点 \(dfn\) 的相对大小顺序和他们在树上的顺序是一样的。 -
虚树的点数是 \(O(k)\) 的,这决定了它可以应用于 \(k\) 与 \(n\) 相比特别少的情况(不同阶)。
-
虚树上需要有关键点和关键点两两求 \(\text{LCA}\) 的结果,这决定了它可以应用于关键点路径的问题。
-
所求的路径信息可以用较小复杂度的信息概况(一般是 \(O(1)\),应该也可以是 \(O(\log n)\)),这决定了我们可以把原图上一个不含关键点的路径缩成虚树上一个边。
而我们有方法得到点数 \(\le 2 \times k - 1\) 的虚树。
建树做法 1
概述
因为对于已知的 \(k\) 个关键点,其构造出的虚树应当包括(也应该只有)关键点和关键点两两求 \(\text{LCA}\) 的结果,所以我们可以先预处理出这些点。
我们不能直接枚举关键点 \(u, v\) 计算 \(\text{LCA}(u, v)\),这样是 \(O(k ^ 2 \times 单次 \text{LCA} 复杂度)\) 的。
我们利用 dfs 序的性质,可以在按照 dfn 排序后,只求出相邻两个关键点的 \(\text{LCA}\),可以证明我们能够得到所有的 \(\text{LCA}\) 结果。
证明:
记关键点序列为 $p$。记 \(S\) 为 \(\{ \text{LCA}(p_i, p_{i + 1}) \}, \forall i \in [l, r)\)。
证明:$\text{LCA}(p_l, p_r) \in S $:
记 \(u = \text{LCA}(p_l, p_r)\)。
首先,因为 \(p_l\) 到 \(p_r\) 的这些点是 \(dfn\) 递增的,而 \(p_l\)、\(p_r\) 都在 \(u\) 的子树内。
那么在遍历完 \(p_l\),没遍历到 \(p_r\) 时,一定都在 \(u\) 的子树内游荡,因为你 dfs 必须先走遍完整的子树再离开。
所以,\(S\) 中 \(dfn\) 最小的不会小于 \(dfn_{u}\)。然后,我们证明 \(\exists i \in [l, r), \text{LCA}(p_i, p_{i + 1}) = u\)。
反证,如果不存在,那么 \(S\) 中的所有点的深度都 \(\gt dep_{u}\),
这意味着,\(\forall i \in [l, r), p_i\) 和 \(p_{i + 1}\) 都在 \(u\) 的同一个儿子 \(v\) 的子树内,否则他们的 \(\text{LCA}\) 就是 \(u\) 了,这与假设矛盾。
也就是说,\(p_l\) 遍历到 \(p_r\) 始终在 \(v\) 的子树内,这意味着 \(v\) 是 \(p_l, p_r\) 的公共祖先且深度 \(\gt dep_u\),那么 \(u \not = \text{LCA}(p_l, p_r)\)。
证毕。证毕。
那么就是说,相邻两个关键点求 \(\text{LCA}\) 就能得到两两求 \(\text{LCA}\) 的结果。
求出了出现在虚树上的点有哪些,我们就能建树了。
下文中记 \(np\) 是虚树上点的集合。
我们知道,在一个树上,对于一个点 \(u\),\(fa_u\) 在 \(v\) 到根的链上,其中 \(dfn_v = dfn_u - 1\)。
或者说,\(fa_u = \text{LCA}(v, u)\)。
又根据虚树上点 \(dfn\) 相对顺序和原树上一样的结论,记 \(dfn'_u\) 为 \(u\) 在虚树上的 \(dfn\)。
将得到的在虚树上的点按照 \(dfn\) 排序,\(dfn'_{np_{i - 1}} = dfn'_{np_i} - 1\),\(\text{LCA}(np_{i - 1}, np_i)\) 就是 \(np_i\) 在虚树上的父亲。
可以参考下图理解:
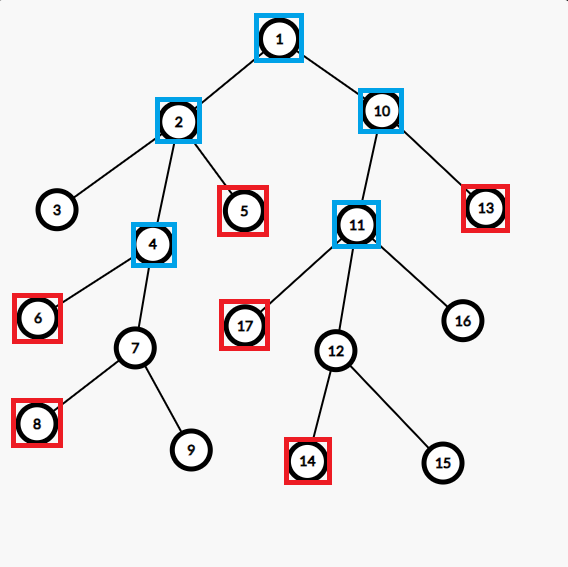
本图中,红色点是关键点,蓝色点是虚树上非关键点的点。
实现
int k; // 关键点个数
vector<int> p, np; // p: 关键点 | np: 求出的虚树上的点
struct edge{
int v, w;
};
vector<edge> vtr[N];
int rt;
void add(int u, int v){
vtr[u].push_back({v, dep[v] - dep[u]}); // dep[v] - dep[u] 求出 u -> v 路径长度
}
void build(){
np.clear();
for(int u : p){
np.push_back(u);
}
sort(p.begin(), p.end(), [](int u, int v){
return dfn[u] < dfn[v];
});
rep(i, 0, k - 2){
int LCA = lca(p[i], p[i + 1]);
np.push_back(LCA);
if(dep[LCA] < dep[rt] || rt == 0){
rt = LCA;
}
}
sort(np.begin(), np.end(), [](int u, int v){
return dfn[u] < dfn[v];
});
np.erase(unique(np.begin(), np.end()), np.end());
rep(i, 0, np.size() - 2){
add(lca(np[i], np[i + 1]), np[i + 1]);
}
}
[HEOI2014] 大工程
题意
给你一个 \(n\) 个点的树。
\(q\) 次询问,给出 \(k\) 和 \(k\) 个点,分别求:
-
两两路径长度的和。
-
两两路径中长度最小值。
-
两两路径中长度最大值。
\(n \le 10 ^ 6, q \le 5 \times 10 ^ 4, \sum k \le 2 \times n\)。
思路
虚树板子题。
显然我们需要 dp 来解决这个问题。
如果我们每次都在 \(n\) 个点的树上跑 dp,复杂度 \(O(nq)\),这不是追忆所以你不能过。
我们研究的是路径问题,一个路径可以容易的缩成一条边权为路径长度的边,且 \(n\) 和 \(k\) 的均摊不同阶,这启发我们思考虚树。
建出虚树后 dp,对于点 \(u\),依次合并进每一个儿子 \(v\) 的子树,合并前时候记录「已合并部分中关键点」和「\(v\) 子树内关键点」组成路径的贡献。
具体地:
ll res_sum, res_mx, res_mn;
ll sum[N], mn[N], mx[N];
void dfs(int u){
for(edge E : vtr[u]){
int v = E.v, w = E.w;
dfs(v);
res_sum += (1ll * sum[u] * cnt[v]) + (1ll * sum[v] * cnt[u]) + 1ll * (cnt[u] * cnt[v]) * w;
res_mx = max(res_mx, (ll)mx[u] + mx[v] + w);
res_mn = min(res_mn, (ll)mn[u] + mn[v] + w);
sum[u] += sum[v] + 1ll * cnt[v] * w;
mx[u] = max(mx[u], (ll)mx[v] + w);
mn[u] = min(mn[u], (ll)mn[v] + w);
cnt[u] += cnt[v];
}
}
代码
点击查看代码
const int N = 1e6 + 5;
const ll inf = 0x3f3f3f3f3f3f3f3f;
int n, q;
vector<int> tr[N];
int dep[N];
int st[N][21];
int dfn[N], dfncnt;
int lg[N];
void init_dfs(int u, int Fa){
st[dfncnt][0] = Fa;
dfn[u] = ++dfncnt;
dep[u] = dep[Fa] + 1;
for(int v : tr[u]){
if(v == Fa) continue;
init_dfs(v, u);
}
}
int cmp(int u, int v){
return dfn[u] < dfn[v] ? u : v;
}
void init_lca(){
lg[1] = 0;
rep(i, 2, n){
lg[i] = lg[i >> 1] + 1;
}
rep(j, 1, lg[n]){
rep(i, 1, n - (1 << j)){
st[i][j] = cmp(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
}
}
int lca(int u, int v){
if(dfn[u] > dfn[v]) swap(u, v);
int p = lg[dfn[v] - dfn[u]];
return (u == v) ? u : cmp(st[dfn[u]][p], st[dfn[v] - (1 << p)][p]);
}
int k;
vector<int> p, np;
struct edge{
int v, w;
};
vector<edge> vtr[N];
int rt;
ll cnt[N]; // special point count
void add(int u, int v){
vtr[u].push_back({v, dep[v] - dep[u]});
}
void build(){
np.clear();
for(int u : p){
np.push_back(u);
}
sort(p.begin(), p.end(), [](int u, int v){
return dfn[u] < dfn[v];
});
rep(i, 0, k - 2){
int LCA = lca(p[i], p[i + 1]);
np.push_back(LCA);
if(dep[LCA] < dep[rt] || rt == 0){
rt = LCA;
}
}
sort(np.begin(), np.end(), [](int u, int v){
return dfn[u] < dfn[v];
});
np.erase(unique(np.begin(), np.end()), np.end());
rep(i, 0, np.size() - 2){
add(lca(np[i], np[i + 1]), np[i + 1]);
}
}
ll res_sum, res_mx, res_mn;
ll sum[N], mn[N], mx[N];
void dfs_vt(int u){
for(edge E : vtr[u]){
int v = E.v, w = E.w;
dfs_vt(v);
res_sum += (1ll * sum[u] * cnt[v]) + (1ll * sum[v] * cnt[u]) + 1ll * (cnt[u] * cnt[v]) * w;
res_mx = max(res_mx, (ll)mx[u] + mx[v] + w);
res_mn = min(res_mn, (ll)mn[u] + mn[v] + w);
sum[u] += sum[v] + 1ll * cnt[v] * w;
mx[u] = max(mx[u], (ll)mx[v] + w);
mn[u] = min(mn[u], (ll)mn[v] + w);
cnt[u] += cnt[v];
}
}
void init(){
res_mn = inf, res_mx = -inf, res_sum = 0;
for(int u : np){
sum[u] = 0, mn[u] = inf, mx[u] = -inf;
}
for(int u : p){
cnt[u] = 1;
mn[u] = mx[u] = 0;
}
}
void clear(){
rt = 0;
res_sum = res_mx = res_mn = 0;
for(int u : np){
vtr[u].clear();
cnt[u] = 0;
sum[u] = mn[u] = mx[u] = 0;
}
vector<int>().swap(p);
vector<int>().swap(np);
}
void solve_test_case(){
n = read();
rep(i, 1, n - 1){
int u = read(), v = read();
tr[u].push_back(v);
tr[v].push_back(u);
}
init_dfs(1, 0);
init_lca();
q = read();
while(q--){
k = read();
p.clear();
rep(i, 1, k) p.push_back(read());
build();
init();
dfs_vt(rt);
write(res_sum, ' ');
write(res_mn, ' ');
write(res_mx, '\n');
clear();
}
}
[CF613D] Kingdom and its Cities
题意
给你一个 \(n\) 个点的树。
\(q\) 次查询,给出 \(k\) 和 \(k\) 个点。
你可以删除一个点和连接它的边,求至少删除多少点才能使得 \(k\) 个点两两不连通。
\(n, q, \sum k \le 10 ^ 5\)。
思路
和上一题类似,可以想到虚树。
建出虚树,进行 dp,\(f_u\) 表示把 \(u\) 子树内关键点断开的最小次数。
分类讨论:
-
\(u\) 是关键点,枚举每个儿子 \(v\),依次考虑。
-
\(v\) 的子树内还有关键点 \(p\) 和 \(v\) 未断开,那么需要在 \(u \rightarrow p\) 的路径上断一个点。
找不到这个点当且仅当 \(v\) 自己就是关键点且 \(w _ {(u, v)} \le 1\)(边权是路径上不含路径端点的点的数量),判无解。
其他情况 \(f_u \leftarrow f_u + f_v + 1\)。 -
否则不用管 \(v\),\(f_u \leftarrow f_u + f_v\)。
-
-
\(u\) 不是关键点,一起考虑所有儿子。
-
只有 \(\le 1\) 个 \(u\) 的儿子 \(v\) 满足 \(v\) 子树内还有关键点和 \(v\) 联通,不用管,\(f_u \leftarrow \sum f_v\)。
满足上述条件的 \(v\) 的个数 \(= 1\) 时需要把 \(u\) 的「子树内有关键点和子树的根相连」标记记为 true。
-
否则就要把 \(u\) 自己断了,\(f_u \leftarrow \left( \sum f_v \right) + 1\)。
-
代码
点击查看代码
const int N = 1e6 + 5;
const int inf = 0x3f3f3f3f;
int n, q;
vector<int> tr[N];
int dep[N], fa[N][21];
int dfn[N], dfncnt;
void init_dfs(int u, int Fa){
dfn[u] = ++dfncnt;
fa[u][0] = Fa;
dep[u] = dep[Fa] + 1;
rep(j, 1, 20){
fa[u][j] = fa[fa[u][j - 1]][j - 1];
}
for(int v : tr[u]){
if(v == Fa) continue;
init_dfs(v, u);
}
}
int lca(int u, int v){
if(dep[u] < dep[v]) swap(u, v);
per(j, 20, 0){
if(dep[fa[u][j]] >= dep[v]){
u = fa[u][j];
}
}
if(u == v) return u;
per(j, 20, 0){
if(fa[u][j] != fa[v][j]){
u = fa[u][j];
v = fa[v][j];
}
}
return fa[u][0];
}
int k;
vector<int> p, np;
struct edge{
int v, w;
};
vector<edge> vtr[N];
int rt;
void add(int u, int v){
vtr[u].push_back({v, dep[v] - dep[u]});
}
void build(){
np.clear();
for(int u : p){
np.push_back(u);
}
sort(p.begin(), p.end(), [](int u, int v){
return dfn[u] < dfn[v];
});
rep(i, 0, k - 2){
int LCA = lca(p[i], p[i + 1]);
np.push_back(LCA);
if(dep[LCA] < dep[rt] || rt == 0){
rt = LCA;
}
}
sort(np.begin(), np.end(), [](int u, int v){
return dfn[u] < dfn[v];
});
np.erase(unique(np.begin(), np.end()), np.end());
rep(i, 0, np.size() - 2){
int LCA = lca(np[i], np[i + 1]);
add(lca(np[i], np[i + 1]), np[i + 1]);
}
}
int ans;
bool no_solution;
int dp[N];
bool link[N], is[N];
void dfs_vt(int u){
int cnt_link = 0;
for(edge E : vtr[u]){
int v = E.v, w = E.w;
dfs_vt(v);
dp[u] += dp[v];
if(is[u]){
if(link[v] == 1){
dp[u]++;
}
if(is[v] && w <= 1) no_solution = 1;
}else{
cnt_link += (link[v] == 1);
}
}
if(!is[u]){
if(cnt_link >= 2){
dp[u]++;
}else if(cnt_link == 1){
link[u] = 1;
}else{
link[u] = 0;
}
}
}
void init(){
no_solution = 0;
ans = 0;
for(int u : p){
is[u] = 1;
link[u] = 1;
}
}
void clear(){
no_solution = 0;
ans = 0;
rt = 0;
for(int u : np){
vtr[u].clear();
is[u] = link[u] = 0;
dp[u] = 0;
}
}
void solve_test_case(){
n = read();
rep(i, 1, n - 1){
int u = read(), v = read();
tr[u].push_back(v);
tr[v].push_back(u);
}
init_dfs(1, 0);
q = read();
while(q--){
k = read();
p.clear();
rep(i, 1, k) p.push_back(read());
if(k == 1){
puts("0");
continue;
}
build();
init();
dfs_vt(rt);
if(no_solution) puts("-1");
else write(dp[rt]);
clear();
}
}
[NOI2021] 庆典
题意
给你一个 \(n\) 个点 \(m\) 条边的有向图,初始时边有如下性质:
-
记 \(x\) 可以到达 \(y\) 为 \(x \Rightarrow y\)。
\(\forall x, y, z\) 若 \(x \Rightarrow z \land y \Rightarrow z\),则 \(x \Rightarrow y\) 或 \(y \Rightarrow x\)。
\(q\) 次询问,给出 \(s, t\),并给出 \(k\) 条新的边(新的边可以不满足原图条件),
查询在 \(s\) 到 \(t\) 的任意一条路径上的点的个数。
\(n, q \le 3 \times 10 ^ 5, n - 1 \le m \le 6 \times 10 ^ 5, 0 \le k \le 2\)。
思路
首先容易想到强连通分量缩点。
然后我们得到了一个 DAG,但是这个 DAG 上我们的原图性质没有用处。
我们思考,现在我们研究的东西是图上点的连通性,那么在保证连通性不变的情况下,我们可以删掉一些没用的边。
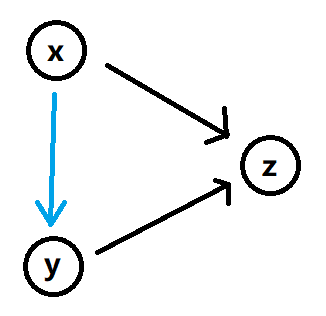
对于每一个 \(z\),满足 \(z\) 的入度 \(\ge 2\),那么就能找到 \(x, y\),满足 \((x, z), (y, z) \in E\)。
那么根据原图的性质,\(x \Rightarrow y\),这时如果删掉了 \((x, z)\) 这条边是不会影响连通性的。
那么我们把 DAG 上所有这种情况都减去一条边,所有点的入度都会 \(\le 1\),我们就得到了一棵树,边是父亲指向儿子的有向边。
代码实现中,可以通过拓扑排序的方式,只保留 \(u\) 被删除的时候(度变为 \(0\))的入边。
定义每个询问的关键点为 \(s, t\) 和 \(k\) 条边的起点、终点。
先把所有子树内没有关键点的子树全删掉,这显然没有影响。
那么此时所有的不含关键点的路径,无论有没有那 \(k\) 条边的加入,都是全部走不到或者全部走的到,且加入前后状态相同。
于是我们可以全部缩掉,建出虚树。
我们把 \(k\) 条边连上,变成了“虚图”,我们直接在虚图及其反图上跑出 \(s\) 能到的点和能到 \(t\) 的点,取其交际计算权值和即可。
这里把路径上的点权值和当作边权,多计算边权的贡献就行了。
时间复杂度 \(\mathcal{O}(q + \sum k)\),你发现 \(k\) 其实不一定要有 \(\le 2\) 的限制。
代码
点击查看代码
const int N = 3e5 + 5;
const int M = 6e5 + 5;
int n, m, q, k;
namespace gr1{ // 原图
vector<int> gr[N];
void add(int u, int v){
gr[u].push_back(v);
}
int dfn[N], dfn_cnt, low[N];
int stk[N], top;
bool in_stk[N];
int scc_cnt, scc_id[N], scc_siz[N];
void tarjan(int u){
dfn[u] = ++dfn_cnt;
low[u] = dfn[u];
stk[++top] = u;
in_stk[u] = 1;
for(int v : gr[u]){
if(!dfn[v]){
tarjan(v);
low[u] = min(low[u], low[v]);
}else if(in_stk[v]){
low[u] = min(low[u], dfn[v]);
}
}
if(low[u] == dfn[u]){
int cur_id = ++scc_cnt;
do{
scc_id[stk[top]] = cur_id;
in_stk[stk[top]] = 0;
scc_siz[cur_id]++;
} while(stk[top--] != u);
}
}
};
namespace gr3{ // gr2 拓扑排序后的树
int n, rt;
vector<int> gr[N];
void add(int u, int v){
gr[u].push_back(v);
}
int sum[N];
int st[N][21];
int dfn[N], dfn_cnt;
void init_dfs(int u, int fa){
st[dfn_cnt][0] = fa;
dfn[u] = ++dfn_cnt;
for(int v : gr[u]){
sum[v] = sum[u] + gr1::scc_siz[v];
init_dfs(v, u);
}
}
void debug(){
fprintf(stderr, "n: %d\n", n);
rep(u, 1, n){
for(int v : gr[u]){
fprintf(stderr, "edge: u: %d, v: %d\n", u, v);
}
}
}
int lg[N];
int cmp(int u, int v){
return dfn[u] < dfn[v] ? u : v;
}
void init_lca(){
lg[1] = 0;
rep(i, 2, n){
lg[i] = lg[i >> 1] + 1;
}
rep(j, 1, lg[n]){
rep(i, 1, n - (1 << j) + 1){
st[i][j] = cmp(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
}
}
int lca(int u, int v){
if(u == v) return u;
if(dfn[u] > dfn[v]) swap(u, v);
int p = lg[dfn[v] - dfn[u]];
return cmp(st[dfn[u]][p], st[dfn[v] - (1 << p)][p]);
}
}
namespace gr2{ // gr1 缩点后
int n;
int deg[N];
vector<int> gr[N];
void add(int u, int v){
gr[u].push_back(v);
}
void unique_edge(){
rep(u, 1, n){
sort(gr[u].begin(), gr[u].end());
gr[u].erase(unique(gr[u].begin(), gr[u].end()), gr[u].end());
for(int v : gr[u]){
deg[v]++;
}
}
}
void topo(){
queue<int> q;
rep(u, 1, n){
if(!deg[u]){
q.push(u);
}
}
while(!q.empty()){
int u = q.front(); q.pop();
for(int v : gr[u]){
if(!--deg[v]){
q.push(v);
gr3::add(u, v);
}
}
}
}
void debug(){
fprintf(stderr, "n: %d\n", n);
rep(u, 1, n){
for(int v : gr[u]){
fprintf(stderr, "edge: u: %d, v: %d\n", u, v);
}
}
}
}
namespace gr4{ // 虚树正向图
int n;
int head[N], e_tot;
struct edge{
int u, v, w, nxt;
} e[M];
void add(int u, int v, int w){
e[++e_tot] = {u, v, w, head[u]};
head[u] = e_tot;
}
bool vis[N];
bool vis_e[M];
void bfs(int st){
queue<int> q;
q.push(st);
vis[st] = 1;
while(!q.empty()){
int u = q.front(); q.pop();
for(int i = head[u]; i; i = e[i].nxt){
vis_e[i] = 1;
int v = e[i].v, w = e[i].w;
if(!vis[v]){
vis[v] = 1;
q.push(v);
}
}
}
}
void debug(){
fprintf(stderr, "debug gr4, e_tot: %d\n", e_tot);
rep(i, 1, e_tot){
fprintf(stderr, "i: %d, u: %d, v: %d, w: %d\n", i, e[i].u, e[i].v, e[i].w);
}
}
}
namespace gr5{ // 虚树反向图
int n;
int head[N], e_tot;
struct edge{
int u, v, w, nxt;
} e[M];
void add(int u, int v, int w){
e[++e_tot] = {u, v, w, head[u]};
head[u] = e_tot;
}
bool vis[N];
bool vis_e[M];
void bfs(int st){
queue<int> q;
q.push(st);
vis[st] = 1;
while(!q.empty()){
int u = q.front(); q.pop();
for(int i = head[u]; i; i = e[i].nxt){
vis_e[i] = 1;
int v = e[i].v, w = e[i].w;
if(!vis[v]){
vis[v] = 1;
q.push(v);
}
}
}
}
void debug(){
fprintf(stderr, "debug gr5, e_tot: %d\n", e_tot);
rep(i, 1, e_tot){
fprintf(stderr, "i: %d, u: %d, v: %d, w: %d\n", i, e[i].u, e[i].v, e[i].w);
}
}
}
int p[N], np[N], p_siz, np_siz;
void solve(){
int s = read(), t = read();
s = gr1::scc_id[s], t = gr1::scc_id[t];
// deb(s, t);
p[++p_siz] = s, p[++p_siz] = t;
np[++np_siz] = s, np[++np_siz] = t;
rep(i, 1, k){
int u = read(), v = read();
u = gr1::scc_id[u], v = gr1::scc_id[v];
// deb(u, v);
gr4::add(u, v, 0);
gr5::add(v, u, 0);
p[++p_siz] = u, p[++p_siz] = v;
np[++np_siz] = u, np[++np_siz] = v;
}
sort(p + 1, p + p_siz + 1, [](int u, int v){
return gr3::dfn[u] < gr3::dfn[v];
});
// fprintf(stderr, "debug p\n");
// rep(i, 1, p_siz){
// fprintf(stderr, "i: %d, p[i]: %d\n", i, p[i]);
// }
rep(i, 1, p_siz - 1){
np[++np_siz] = gr3::lca(p[i], p[i + 1]);
}
sort(np + 1, np + np_siz + 1, [](int u, int v){
return gr3::dfn[u] < gr3::dfn[v];
});
np_siz = unique(np + 1, np + np_siz + 1) - np - 1;
// fprintf(stderr, "debug np\n");
// rep(i, 1, np_siz){
// fprintf(stderr, "i: %d, np[i]: %d\n", i, np[i]);
// }
rep(i, 1, np_siz - 1){
int u = gr3::lca(np[i], np[i + 1]), v = np[i + 1];
// fprintf(stderr, "add edge: u: %d, v: %d\n", u, v);
gr4::add(u, v, gr3::sum[v] - gr1::scc_siz[v] - gr3::sum[u]);
gr5::add(v, u, gr3::sum[v] - gr1::scc_siz[v] - gr3::sum[u]);
}
// cerr << "virtual tree has been built\n";
// gr4::debug(), gr5::debug();
gr4::bfs(s), gr5::bfs(t);
int ans = 0;
rep(i, 1, np_siz){
int u = np[i];
if(gr4::vis[u] && gr5::vis[u]){
ans += gr1::scc_siz[u];
}
}
rep(i, 1, gr4::e_tot){
if(gr4::vis_e[i] && gr5::vis_e[i]){
ans += gr4::e[i].w;
}
}
write(ans);
rep(i, 1, np_siz){
int u = np[i];
gr4::head[u] = 0;
gr4::vis[u] = 0;
gr5::head[u] = 0;
gr5::vis[u] = 0;
}
rep(i, 1, gr4::e_tot){
gr4::vis_e[i] = gr5::vis_e[i] = 0;
}
gr4::e_tot = gr5::e_tot = 0;
p_siz = np_siz = 0;
}
void solve_test_case(){
n = read(), m = read(), q = read(), k = read();
rep(i, 1, m){
int u = read(), v = read();
gr1::add(u, v);
}
rep(u, 1, n){
if(!gr1::dfn[u]){
gr1::tarjan(u);
}
}
// fprintf(stderr, "debug gr1's tarjan result: scc_cnt: %d\n", gr1::scc_cnt);
// rep(u, 1, n){
// fprintf(stderr, "u: %d, scc_id[u]: %d\n", u, gr1::scc_id[u]);
// }
// rep(u, 1, gr1::scc_cnt){
// fprintf(stderr, "u: %d, scc_siz[u]: %d\n", u, gr1::scc_siz[u]);
// }
gr2::n = gr3::n = gr4::n = gr5::n = gr1::scc_cnt;
rep(u, 1, n){
for(int v : gr1::gr[u]){
// int u = gr1::e[i].u, v = gr1::e[i].v;
if(gr1::scc_id[u] == gr1::scc_id[v]) continue;
gr2::add(gr1::scc_id[u], gr1::scc_id[v]);
}
}
gr2::unique_edge();
// gr2::debug();
gr2::topo();
// gr3::debug();
gr3::rt = gr1::scc_cnt;
gr3::sum[gr3::rt] = gr1::scc_siz[gr3::rt];
gr3::init_dfs(gr3::rt, 0);
gr3::init_lca();
while(q--){
solve();
}
}
/*
5 6 4 1
1 2
1 3
1 4
2 5
4 5
5 4
1 4 5 1
2 3 5 3
1 2 5 2
3 4 5 1
4
4
4
0
---
5 6 1 1
1 2
1 3
1 4
2 5
4 5
5 4
2 3 5 3
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号