SZMS 251019 订题赛笔记
串串
题意
给定 \(n\) 个长度为 4 的字符串,你需要找出有多少对字符串满足恰好 \(d\) 个对应位置的字符不同。
\(n \le 5 \times 10 ^ 4, d \le 4\)。
思路
前面忘了。
注意到恰好。
注意到容易钦定若干位置相同。
注意到我们学过一个东西叫做 two tasty shit reverse act。
后面忘了。
因为你钦定不同不好做,直接改成询问多少个相同。(注意到 \(|t_1| = |t_2|\))
认真点,\(f_i\) 表示钦定 \(i\) 个相同,\(g_i\) 表示恰好 \(i\) 个相同。
后面不是忘了,是真没了。
代码
#define int ll
const int N = 5e4 + 5;
int n, d;
string s[N];
map<string, int> cnt[16];
int c[5][5] = {
{1, 0, 0, 0, 0},
{1, 1, 0, 0, 0},
{1, 2, 1, 0, 0},
{1, 3, 3, 1, 0},
{1, 4, 6, 4, 1}
};
void solve_test_case(){
cin >> n >> d;
d = 4 - d;
rep(i, 1, n){
cin >> s[i];
}
ll ans = 0;
rep(i, 1, n){
// ll res = 0;
rep(S, 0, 15){
string tmp = "";
int popcnt = 0;
per(j, 3, 0){
if(S & (1 << j)){
tmp = tmp + s[i][j];
popcnt++;
}
}
ans += c[popcnt][d] * ((popcnt - d) % 2 == 1 ? -1 : 1) * cnt[S][tmp];
// cnt[popcnt][tmp]++;
}
rep(S, 0, 15){
string tmp = "";
int popcnt = 0;
per(j, 3, 0){
if(S & (1 << j)){
tmp = tmp + s[i][j];
popcnt++;
}
}
// ans += c[popcnt][d] * ((popcnt - d) % 2 == 1 ? -1 : 1) * cnt[popcnt][tmp];
cnt[S][tmp]++;
}
// deb(ans);
}
write(ans);
}
小 B 的诗集
原题:[POI 2018 R2] 诗集 Book of poetry
题意
你有一些文章,长度 \(a_i\) 行,标题占一行。你在印刷它们,每页 \(s\) 行,若标题出现在最后一行则空行翻页。求空行最小值。
\(n, s \le 10 ^ 6\)。
做法
先 \(a_i \leftarrow (a_i + 1) \mod s\)
无法 dp,考虑贪心。
整体不好考虑,考虑局部的一步。
考虑 \(a\) 互不相同,发现到一步,如果还有至少 2 种能用的 \(a\),则必定可以不空行,否则取决于唯一选择。
贪心地选即可。
否则,我们就有重复的 \(a\),为了让以后有更多选择,我们每次保证最优策略情况下,选择剩余个数最多的就好。
代码
#define int ll
const int N = 1e6 + 5;
int n, s;
int a[N];
vector<int> pos[N], ans;
int sum, cnt;
priority_queue<pair<int, int>> q;
void solve_test_case(){
n = read(), s = read();
rep(i, 1, n){
a[i] = (read() + 1) % s;
pos[a[i]].push_back(i);
}
rep(i, 0, s - 1){
if(!pos[i].empty()){
q.push({pos[i].size(), i});
}
}
rep(i, 1, n){
if(sum % s == s - 1){
sum = 0;
cnt++;
}
pair<int, int> mx1 = q.top(); q.pop();
if((sum + mx1.second) % s == s - 1 && !q.empty()){
pair<int, int> mx2 = q.top(); q.pop();
ans.push_back(pos[mx2.second].back());
pos[mx2.second].pop_back();
sum = (sum + mx2.second) % s;
q.push(mx1);
if(!pos[mx2.second].empty()) q.push({pos[mx2.second].size(), mx2.second});
}else{
ans.push_back(pos[mx1.second].back());
pos[mx1.second].pop_back();
sum = (sum + mx1.second) % s;
if(!pos[mx1.second].empty()) q.push({pos[mx1.second].size(), mx1.second});
}
}
write(cnt);
for(int x : ans) write(x, ' ');
}
Journey
原题:[CERC2016] 爵士之旅 Jazz Journey
题意
黑曼巴要去 \(n\) 个城市表演肘击,他的行程是一个长为 \(d\) 的序列 \(a\)。
由于黑曼巴坐飞机太久有概率遇到佐巴扬,所以他总是直飞。
黑曼巴有 \(m\) 个飞行员飞的若干航班,包括:
-
单程票,\(u\) 单向到 \(v\)。
-
双程票,但要求必须先从 \(u\) 到 \(v\) 以后,才可以选择从 \(v\) 到 \(u\)(也就是说可以不飞)。
黑曼巴还需要留钱去【数据删除】,所以请帮他省钱。
\(n, d, m \le 3 \times 10 ^ 5\)。
思路
注意到如果端点集合不同,就独立。
所以只需要考虑两个城市之间互相飞飞飞。
记录一下 \(u\) 飞 \(v\)(和反过来),\(u\) 飞 \(v\) 飞 \(u\)(和反过来)。
为了保证单程换双程一定不劣(懒得特判),并考虑双程当单程用:
u_v = min(u_v, u_v_u);
v_u = min(v_u, v_u_v);
u_v_u = min(u_v_u, u_v + v_u);
v_u_v = min(v_u_v, v_u + u_v);
不妨钦定 u_v_u \(\lt\) v_u_v,然后考虑匹配一些 u -> v,v -> u。
可以类比括号匹配,栈维护。
反过来,把 u -> v 和 v -> u 的信息完全互换即可。
接着,再把 v -> u 和 u -> v 匹配,再把剩下的花费算一下就行了。
代码
#define int ll
const int N = 3e5 + 5;
const int inf = INT_MAX;
int n, d;
int m;
int ans = 0;
struct node{
int u_v, v_u;
int u_v_u, v_u_v;
int cnt[2];
vector<int> vec;
node(){
cnt[0] = cnt[1] = 0;
u_v = v_u = u_v_u = v_u_v = inf;
vec.clear();
}
void ins(int t){ // t = 0 => u -> v | t = 1 => v -> u
cnt[t]++;
vec.push_back(t);
}
int calc(){
if(u_v + v_u < min(u_v_u, v_u_v)){
return cnt[0] * u_v + cnt[1] * v_u;
}
u_v = min(u_v, u_v_u);
v_u = min(v_u, v_u_v);
u_v_u = min(u_v_u, u_v + v_u);
v_u_v = min(v_u_v, v_u + u_v);
vector<int> stk;
if(u_v_u > v_u_v){
for(int &x : vec){
x = 1 - x;
}
swap(u_v, v_u);
}
int res = 0;
for(int x : vec){
if(!stk.empty() && x == 1 && stk.back() == 0){
stk.pop_back();
res += min(u_v_u, v_u_v);
}else{
stk.push_back(x);
}
}
vector<int> stk2;
for(int x : stk){
if(!stk2.empty() && x == 0 && stk2.back() == 1){
stk2.pop_back();
res += max(u_v_u, v_u_v);
}else{
stk2.push_back(x);
}
}
for(int x : stk2){
if(x == 0) res += u_v;
else res += v_u;
}
return res;
}
};
map<pair<int, int>, node> mp;
int a[N];
pair<int, int> key(int x, int y){
return make_pair(min(x, y), max(x, y));
}
vector<pair<int, int>> used;
void solve_test_case(){
n = read(), d = read();
rep(i, 1, d){
a[i] = read();
}
m = read();
rep(i, 1, m){
int u = read(), v = read();
char c = read_c();
int w = read();
used.push_back(key(u, v));
if(c == 'O'){
if(u < v) mp[key(u, v)].u_v = min(mp[key(u, v)].u_v, w);
if(u > v) mp[key(u, v)].v_u = min(mp[key(u, v)].v_u, w);
}else{
if(u < v) mp[key(u, v)].u_v_u = min(mp[key(u, v)].u_v_u, w);
if(u > v) mp[key(u, v)].v_u_v = min(mp[key(u, v)].v_u_v, w);
}
}
rep(i, 1, d - 1){
used.push_back(key(a[i], a[i + 1]));
mp[key(a[i], a[i + 1])].ins((a[i] < a[i + 1]) ? 0 : 1);
}
sort(used.begin(), used.end());
used.erase(unique(used.begin(), used.end()), used.end());
for(pair<int, int> id : used){
ans += mp[id].calc();
}
write(ans);
}
Photo
原题:[JOI 2021 Final] 集体照 / Group Photo
题意
给你一个序列 \(a\),可以邻项交换,使得 \(a_i - a_{i + 1} \ge -1\),求最小交换次数。
\(|a| = n \le 5000\)。
思路
容易发现,最后 \(a\) 要变成形如:
的若干公差为 -1 的数列拼起来。
发现不好直接算这个图形的答案,考虑 dp。
考虑 dp 的转移顺序,下标从小到大状态数显然不对,于是考虑按照值域做 dp。
令 \(dp_i\) 表示把值域 \([1,i]\) 的排到下标 \([1,i]\) 上,保证 \(i\) 是一个等差数列的结尾,此时的最小次数。
转移顺序应当是 \(dp_i \rightarrow dp_j\)。
我们需要计算将区间 \([i+1,j]\) 排好的代价,注意到直接算不好算,那么我们可以利用递推的思想,把 \([i+1, j- 1]\) 的代价递推到 \([i + 1, j]\) 上。
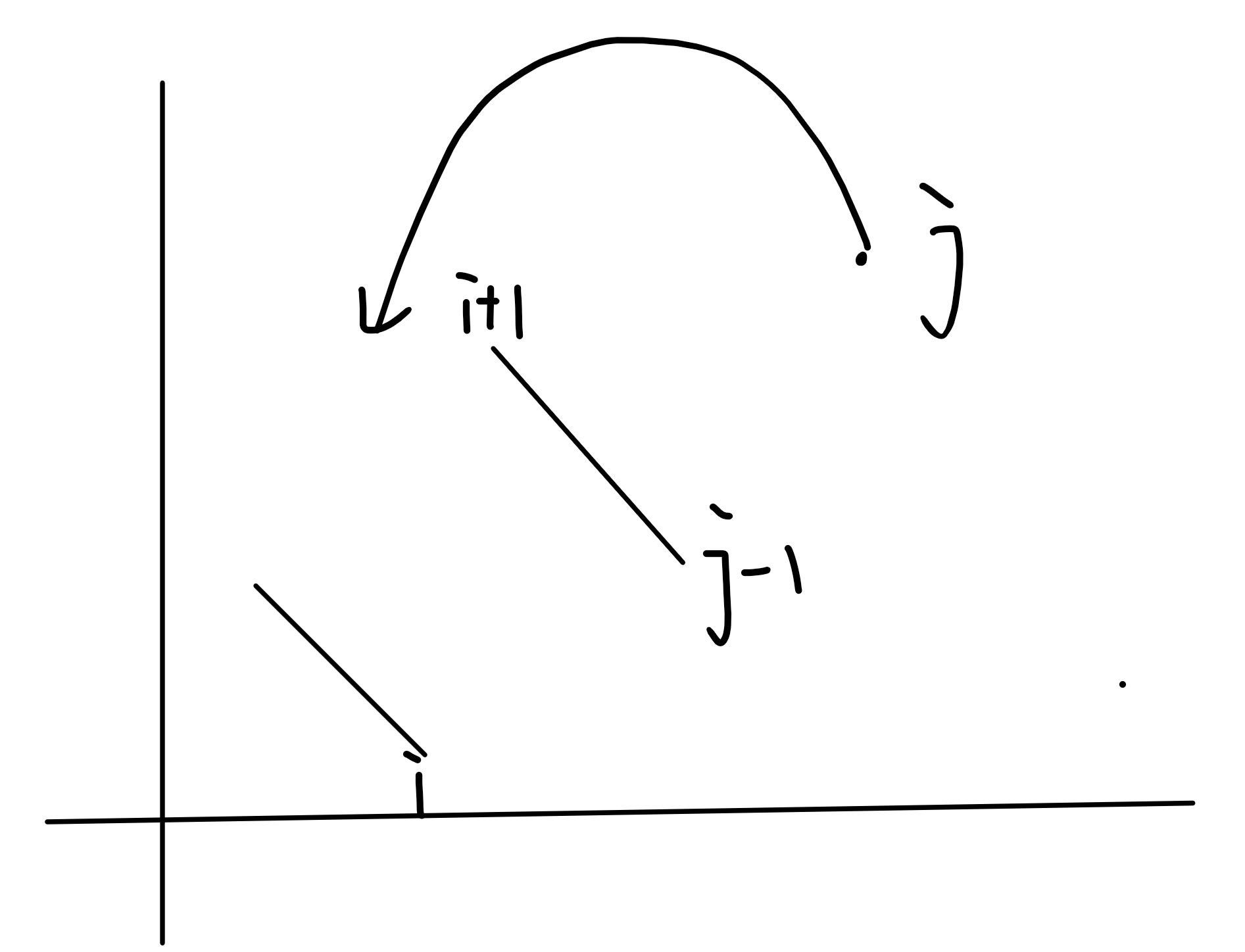
相当于加上 \(j\) 从右边飞到 \(i + 1\) 左边的贡献。
分析这个过程,若一个 \([i + 1, n]\) 中的数在开始的时候是在 \(j\) 左侧,现在 \(j\) 飞过来就变成 \(j\) 的右侧,根据冒泡排序理论应当造成 1 的贡献。
类比冒泡排序理论,定义逆序对 \((x,y)\) 为原序列 \(x\) 在 \(y\) 左侧,新序列 \(x\) 在 \(y\) 右侧。
则此处新产生的代价即为 \(\sum \limits _{i + 1 \le p \le n} [(p, j) 是逆序对]\)。
那么相反的,\(j\) 的移动会使得一些逆序对消失,具体地,是 \(j\) 与 \(p, i + 1 \le p \le j - 1\) 构成逆序对,现在 \(j\) 不在 \(p\) 右侧而摧毁了它。
维护区间和单点构成逆序对个数(第二类可以交换 \(x\) 与 \(y\),转换为统计顺序对个数,进而转换为统计逆序对个数)即可,简单前缀和实现。
那么我们就能递推算出 \([i + 1,j]\) 的代价,进而实现转移。
复杂度 \(O(n ^ 2)\)。
代码
#define int ll
const int N = 5010;
int n;
int a[N];
int pos[N];
int cnt1[N][N], cnt2[N][N];
int f[N];
void solve_test_case(){
n = read();
rep(i, 1, n){
a[i] = read();
pos[a[i]] = i;
}
rep(i, 1, n){
rep(j, 1, n){
cnt1[i][j] = cnt1[i - 1][j] + (pos[i] > pos[j]);
}
}
rep(i, 1, n){
rep(j, 1, n){
cnt2[i][j] = cnt2[i - 1][j] + (pos[i] < pos[j]);
}
}
memset(f, 0x3f, sizeof(f));
f[0] = 0;
rep(i, 0, n - 1){
int res = 0;
rep(j, i + 1, n){
res -= (cnt1[j - 1][j] - cnt1[i][j]);
res += (cnt2[n][j] - cnt2[i][j]);
f[j] = min(f[j], f[i] + res);
}
}
write(f[n]);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号