DP - 状压 dp

例题

P1896 [SCOI2005] 互不侵犯

朴素的 dp 是枚举上一行的放置情况和当前行的放置情况。

朴素的 check 有没有冲突是 \(O(n)\)。

发现可以使用人类智慧位运算。

结论，S & ((S << 1) | (S >> 1)) = 0 \(\Leftrightarrow\) \(S\) 没有相邻的 \(1\)。

这时复杂度 \(O(4 ^ n)\)。

进行优化，因为当前行 \(S_2\) 和 \(S_1\) 不能在任何位都是 \(1\)，直接枚举 \(S_1\) 的补集的子集作为 \(S_2\)。

这时每一位都在 \(S_2\) 或 \(S_1\) 是 \(1\) 或都不是，时间复杂度 \(O(3 ^ n)\)。

发现枚举 \(S_1\) 时还有判断自己有没有相邻 \(1\)，但是没有相邻 \(1\) 的东西是 \(O(\varphi ^ {2n})\) 约为 \(O(2.6 ^ n)\)，优秀无需多盐 /dy

其实可以人类智慧轮廓线 dp，但是想在下一个题里讲。

P5074 Eat the Trees

轮廓线 dp，是插头 dp 的一种。

顾名思义，维护轮廓线（p++）。

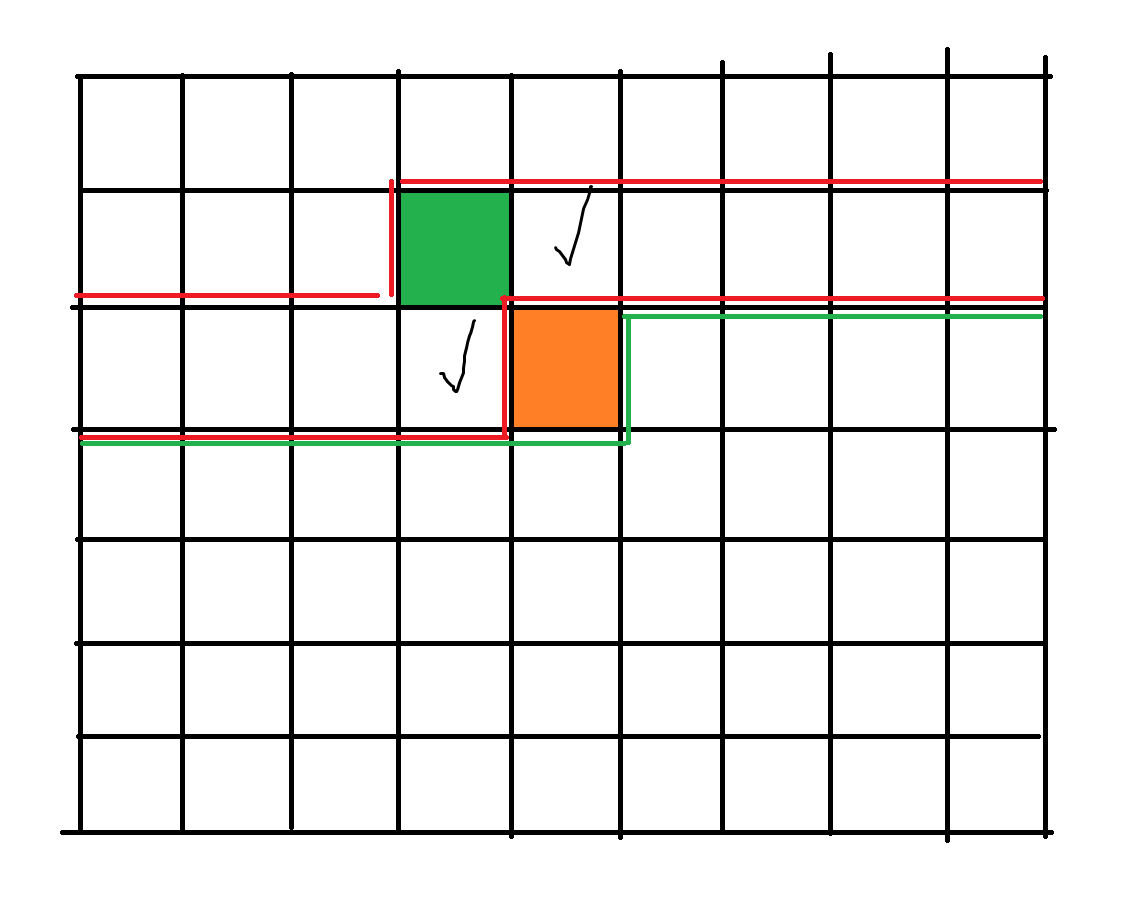
轮廓线就是两条红色线之间的部分。我们枚举的只有这些块的插头，状态 \(O(2 ^ {n + 1})\)

考虑算橙色块的答案，就是看它上面和左边的点的插头（就是最后的闭合曲线在这里的一小块）：

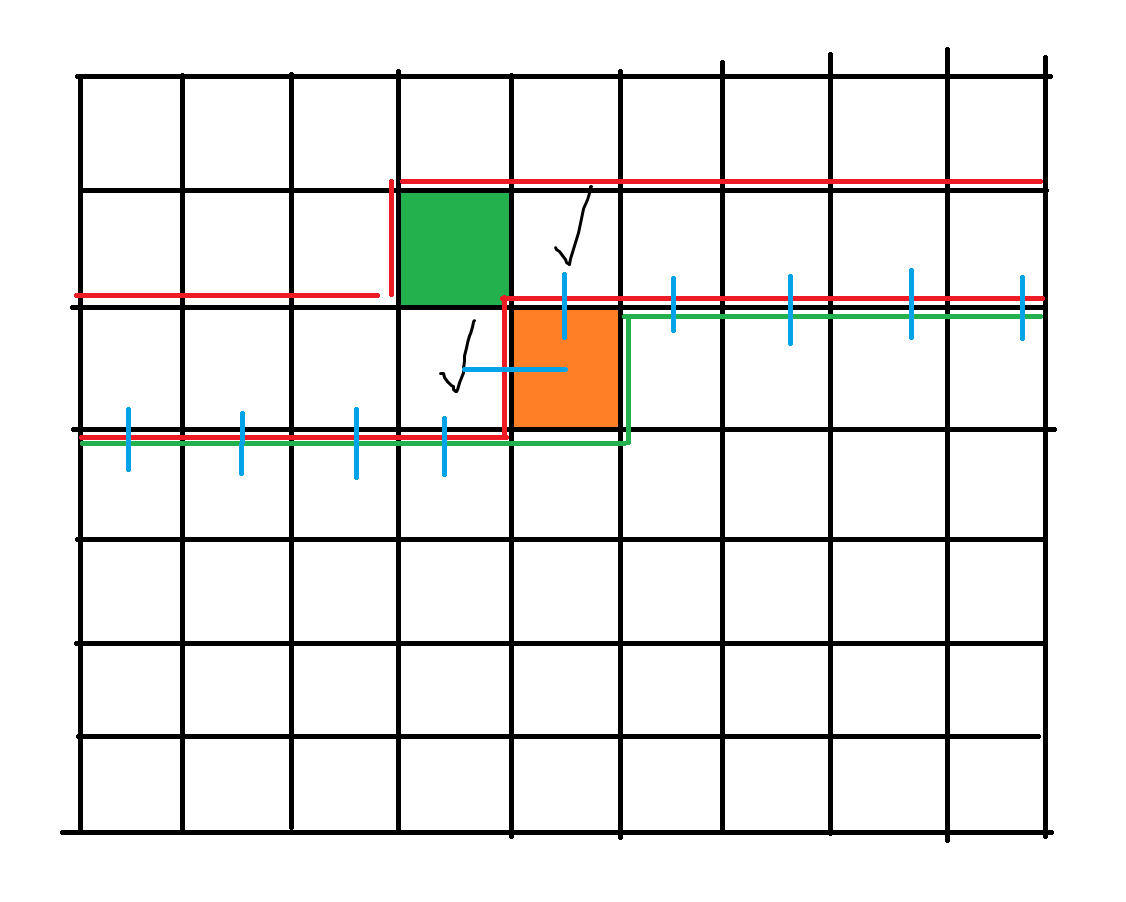
就是蓝色的小线。

• 如果上面和左边都有插头，显然是一个拐角（上拐左）。

• 如果上面和左边都没有插头，就是一个拐角（下拐右）。

• 上面有左边没有，就是直上直下或者上转右。

• 左边有上面没有，就是左右或左转下。

状态的计算很简单，巧用异或就好。

P4590 [TJOI2018] 游园会

QOJ 9619

HDU 6984

AT_dp_o