线段树 tricks

本文主要介绍线段树打标记和维护可合并信息的技巧。

节点维护信息、打标记常见 tricks

区间加，求区间 gcd

由 \(\gcd(a,b)=\gcd(a,a-b)\)，发现区间加不会影响差分数组。

考虑维护差分数组的区间 gcd，这样每次区间 \([l,r]\) 查询后和 \(a_l\) 求一下 gcd 就行了。

区间有无重复数字 / 拓展到满足和（差、积）条件的点对存在性问题

维护每个数字的出现前驱。 \(pre_i\) 表示 \(a_i\) 上一个相同数字出现在 \(pre_i\) 位置。

每次查询 \(\max_{i=l}^r pre_i \lt l\) 则代表没有重复数字。

可以拓展到求满足和（差、积）条件的点对存在性问题。好抽象的表述，我绝对不会告诉你我自己编的这个名字。

这个给道例题 P6617 查找 Search

题面求的是区间内满足和为定值 \(w\) 的点对的存在性。

可以照搬，维护每个点 \(i\) 的前面满足 \(a_j=w-a_i\) 的 \(j\)。记为 \(pre_i\)

但是这样有问题，发现满足 \(i=pre_j\) 的 \(j\) 不是唯一的，这样更新的时候复杂度错误。

发现存在性问题，找一个最容易的就好了。这是再所有 \(j\) 中，只有最靠近 \(i\) 的才有意义。只维护这一个就好，单点修改时只更新它，时间复杂度还是 \(O(1)\)。

是否存在固定个数问题

当需要维护待修改的形如“是否存在一定个数的满足某条件的对象”时，可以维护到达这个个数还剩下的量，这样只需要判断是否归零。

from : Luogu P4090

mex

求解一些什么东西的 mex，可以维护整个值域，维护每个值区间的“可行性”，第一个不可行的就是 mex。

CF1083C

题意

树上每个点有点权，点权构成一个排列（即不重复）。
要支持交换两个点的点权，查询树上所有路径中 mex 的 max。

思路

一个数可以成为 mex 满足 \(\le\) 它的都在一个链上。

线段树维护值域，维护值域中的点是否在一个链上，以及链的端点。合并时分类讨论即可。

查询线段树二分。

线段树合并

适用性

线段树合并一般用来统计图上和树上的信息。

同时，因为线段树合并在线段树中信息比较分散（感性理解）时效率更高，所有一般用在动态开点权值线段树上。

思想

合并两棵线段树 t1、t2 时，按照正常方法递归。到每个节点 x 的时候：

• t1[x] 存在，t2[x] 不存在，则返回 t1[x]。

• t1[x] 不存在，t2[x] 存在，则返回 t2[x]。

• t1[x] 和 t2[x] 都不存在，返回空节点。

• t1[x] 和 t2[x] 都存在，合并两个节点后返回。

例题

P1552 [APIO2012] 派遣

题意：\(n\) 个点组成一棵树，每个点都有一个领导力和费用，可以让一个点当领导，然后在这个点的子树中选择一些费用之和不超过 \(m\) 的点，得到领导的领导力乘选择的点的个数（领导可不被选择）的利润。求利润最大值。\(n \leq 10^5\)。

显然在一个子树里必须要找费用最少的，于是维护权值线段树。

就是在 dfs 过程中，钦定当前点 \(u\) 为领导，每次线段树上二分，找到和 \(\leq m\) 的最多点。更新答案即可。
在 dfs 往上走的时候，合并 \(u\) 的所有儿子的线段树。

线段树维护单调栈

这是一个相当逆天的 trick，拜谢 @Clein.qwq 大神。

适用性

当发现一个问题转换完后（可能是 dp）需要维护一个单调栈，但是需要修改，就可以套用。

这是一个只能全局查询的东西。

UPD 25/07/28: 这个东西完全可以区间查询！！！！！详见例题 2 部分

思想

以下是对于单调递增单调栈的一个狭义介绍。

线段树维护的信息有：

• 区间最大值
• 答案，但是这是个假的答案，是只考虑这个节点对应区间的，不考虑其他区间的影响。

然后我们在 push_up 时考虑加入左侧区间对于右侧区间的影响。

这里设计一个 calc(x, l, r, key) 表示 \(x\) 节点考虑大于 \(key\) 部分的答案。

三种情况分类讨论：

1. 区间长度为 \(1\)：判断该值是否 \(\gt key\) 即可。

2. 左儿子的 \(mx_{ls} \gt key\)：这时右儿子已经考虑过左儿子的影响，一定是每一项大于 \(key\) 的。（考虑左儿子的影响会让它每一项 \(\gt mx_{ls} \gt key\)。）

这时递归左儿子区间，最后直接加上右儿子答案。

3. 左儿子的 \(mx_{ls} \le key\)：这时左儿子肯定全都没有贡献，直接扔进垃圾桶里面~。递归考虑右儿子区间即可。

这个 calc(x, l, r, key) 在 push_up(x) 时调用，具体地是：

int calc(int x, int l, int r, double k){
    if(t[x].mx <= k) return 0;
    if(l == r) return t[x].mx > k;
    if(t[ls(x)].mx > k){
        return calc(ls(x), l, mid, k) + t[x].ans - t[ls(x)].ans;
    }else{
        return calc(rs(x), mid + 1, r, k);
    }
}
void push_up(int x, int l, int r){
    t[x].mx = max(t[ls(x)].mx, t[rs(x)].mx);
    t[x].ans = t[ls(x)].ans + calc(rs(x), mid + 1, r, t[ls(x)].mx);
}

所以 push_up 的复杂度是 \(O(\log n)\)，这也算是一种 trick，即 push_up \(\log\) 化（在题解里看到的，感觉这么说有点 p）。

例题

例题 1：板子：P4198 楼房重建

就是板子题。节点维护的答案是单调栈大小。

例题 2：口胡题

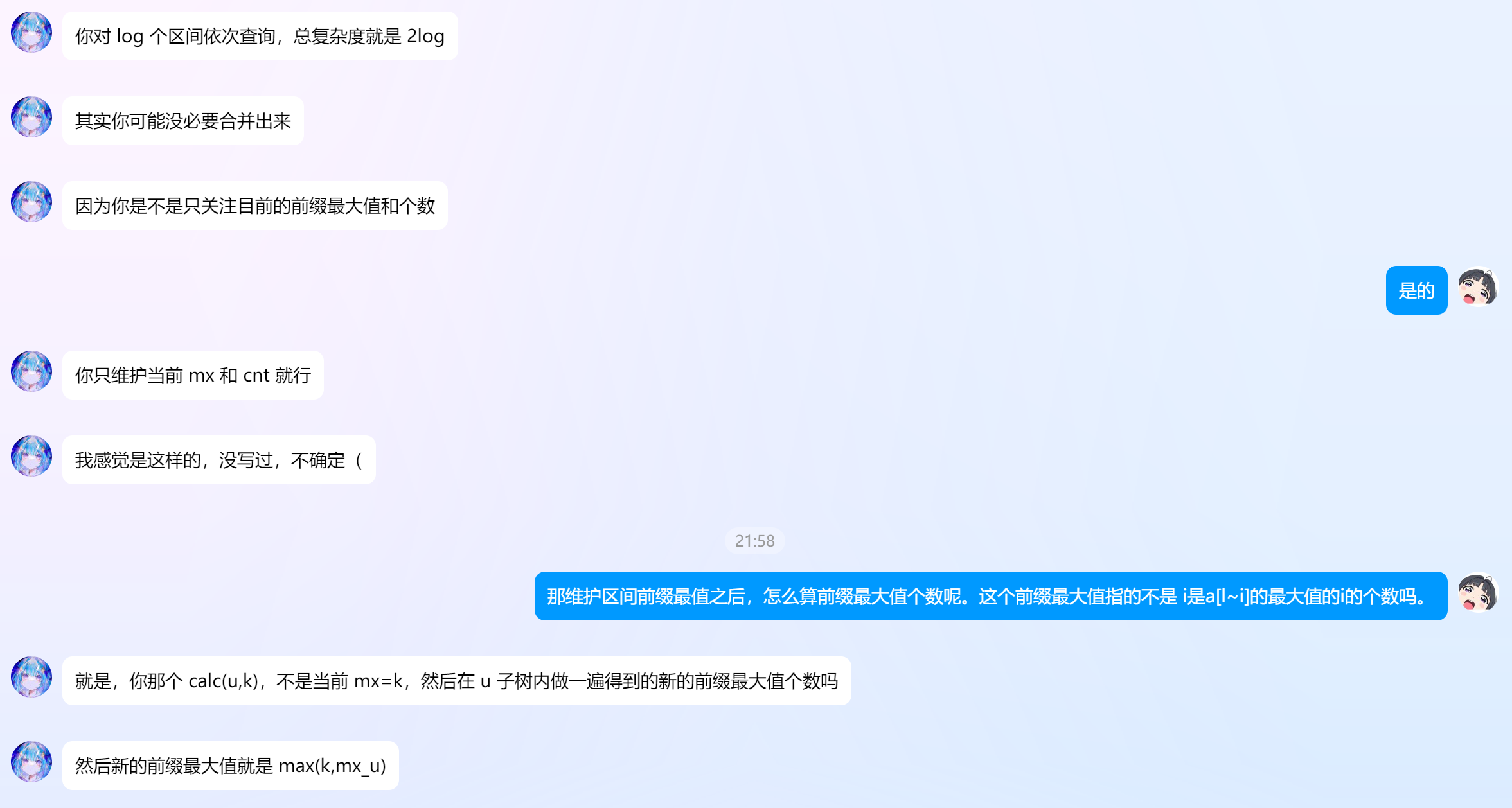
查询任意区间 \([l,r]\) 的前缀最大值个数，前缀最大值个数定义为满足 \(a_i = \max_{j=l}^i a_j\) 的 \(i\) 的个数。

我们模仿楼房重建的办法，线段树维护区间的前缀最大值及个数。

线段树重构

当发现有些修改不好维护，尝试分析修改的区间大小，若发现较小，则考虑重构这一段的线段树。

例题 1：ZR 模拟赛

势能线段树

适用性

对于普通的线段树懒标记，我们需要满足：

• 懒标记快速更新节点维护东西

• 懒标记快速合并

发现有些东西不能做到第一点。

最普遍的例子（好像是绝大多数例子）：

• 区间 mod

• 区间 gcd

• 区间 sqrt

一般是要用到叶子节点的一些操作。

思想

注意到一个东西被修改的次数有限，那么可以暴力去修改，剪枝优化。

复杂度分析就加入每个东西修改次数。

然后我们为了剪枝而维护的信息就叫做势能。

具体例子具体说明。

例题

Luogu P4145

题意：区间 sqrt 操作，区间查询和。

发现一个数被开方很多次之后变成 1，然后继续开方无意义。

维护区间最大值，若为 1 则放弃递归。

代码很简单，就是在 modify 里递归终止于 l == r，但在此之前判断势能。

Codeforces 438D

题意：区间取模区间求和。

还是类似，取模时，若最大值都 \(\lt mod\)，则不会影响。

维护区间最大值的势能即可。

Luogu P9989

题意：区间与 \(x\) 取 gcd，区间查和。

维护区间的 lcm，若 lcm 都是 \(x\) 的因数，那么不影响。

线段树二分

线段树二分是利用线段树自身结构，用来替代二分套线段树判断的，可以让复杂度少一个 log。

思想是很简单的，只是给出一些写代码的技巧。

默认是从特定方向开始找第一个不合法的 / 最后一个合法的

• 一些题要在区间内线段树二分（例：Luogu P9695）

  那么就外面一层遍历，将区间拆成 \(\log n\) 个线段树结点，按照给定顺序合并，若发现该区间不完全合法，那么调用另一个函数，专门求解一个线段树区间内的答案（这个简单递归实现）

• 注意合并的顺序，先朝左还是先朝右会决定合并顺序（尤其是合并不具有交换律的运算）

• 多个线段树叠起来二分（还是 Luogu P9695）

  比如这个题要一堆线段树一起二分，要用到这些线段树的信息来判断。

  可以维护所有线段树上当前节点的编号（动态开点），然后正常二分。