DP 优化 - 整体维护

本文主要介绍 dp 优化方法——整体维护。

算法思想

整体维护的思想就是不去维护每个节点具体的 dp 值，而是将 dp 数组看成一个序列。

常见的是将二维 dp[i][j] 看成是 dp[0]，dp[1]，... 这样的几个序列，利用数据结构维护序列的变化。

第一步：找到要维护的对象（的数学形式）

连续段函数值相同

这里用一个例子进行说明。

考虑一个三角形的转移 \(dp_{i,j} = [op_i == 1] ? \max(dp_{i-1,j},dp_{i-1,j+1}) : \min(dp_{i-1,j},dp_{i-1,j+1})\)。

连续段是一次函数（凸分段一次函数——slope trick）

推荐博客

适用性

如前文所述，slope trick 适用函数须具备一下条件:

• 分段一次函数
• 在定义域内呈凸性（或凹性）
  由此，在维护 dp 时，根据凸函数相加/减凸性不变，可以一直拥有此性质。

在优化 dp 时，dp 式具有一些规律，最典型的就是绝对值函数。

思想

先上定义：slope trick 是维护分段一次凸性函数的每个斜率变化点，规定每个变化点左右函数斜率变化 \(|\Delta k| = 1\)。而对于会让函数斜率变化 \(|\Delta k| \ge 2\) 的，就要拆点成 \(|\Delta k|\) 个。

由于斜率变化点之间有顺序，所以用堆维护，常见的有 std::priority_queue 和 std::multiset。

但是在维护 dp 转移增加决策时，变化点可能让斜率变化 \(+1\) 或 \(-1\)。举个常见的绝对值函数例子:

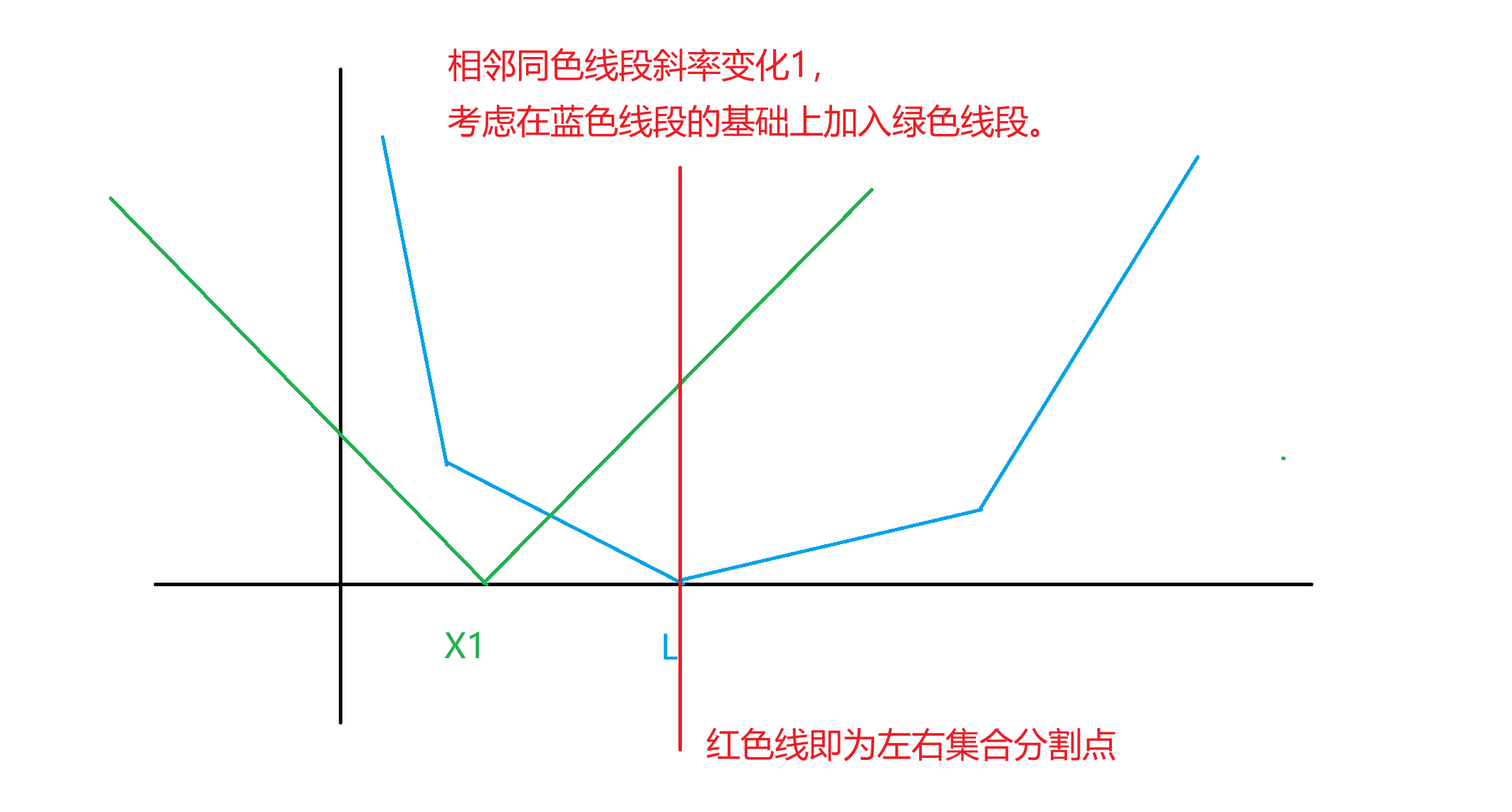
在加入绝对值函数时，会让 \(x \lt x_1\) 的段斜率 \(-1\)，让 \(x \gt x_1\) 的段斜率 \(+1\)。

感性理解，我们要找一个不变的地方，用来确定其他段的斜率。这个段就是斜率为 \(0\) 的段 / 点。

于是能想到以此为中心，分成左右两个堆来维护斜率变化点。

左侧集合的最右边和右侧集合的最左边代表的斜率都是 \(0\)。

---

在不同的问题中，有不同的具体实现。以下是推荐博客原文引用。

• 相加：将 \(f(x_0)\), \(k_0\) 直接相加，斜率变化点的集合直接合并。常用于加一次函数、绝对值函数。

• 取前缀/后缀 \(\min\)：去掉 \(k < 0\) 或 \(k > 0\) 的部分。

• 求 \(\min, \arg\min\)：提取 \(k = 0\) 部分。

• 平移：维护 \(f(x_0)\), \(k_0\) 变化，斜率变化点在全局打平移标记。

• 翻转：维护 \(f(x_0)\), \(k_0\) 变化，斜率变化点在全局打翻转标记。

例题

P11598 Safety

这是一道能较好帮助理解 slope trick 的尽可能多的内涵的题目。包括以上的 相加、求 \(\min\)、平移。

题意：给出一个序列 \(a_i\)，操作是给 \(a_i + 1\) 或 \(-1\)，要求 \(\forall 1 \leq i \lt n, |a_i - a_{i+1}| \leq H\)，其中 \(H\) 为给定常量。问最小代价。

显然考虑动态规划，\(dp_{i,j}\) 表示考虑前 \(i\) 个元素，\(a_i\) 改为 \(j\) 的最小代价。

显然有转移式：

\[dp_{i,j} = \min\limits_{k=j-H}^{j+H}dp_{i-1,k}+|j-a_i| \]

发现可以分成取最小值和加绝对值函数两个部分。

考虑画图寻找规律（这也是发现整体维护的一个办法）。

最小值部分就可以看作是将整个 \(dp_{i-1}\) （如图 1）向左拉扯 \(H\)，向右拉扯 \(H\) 变成图 2 的样子。然后取全局最小值变成图 3 样子。

拉扯这里维护两个 \(tagl,tagr\)，表示下标偏移量。

\[图1 \]

\[图2 \]

\[图3 \]

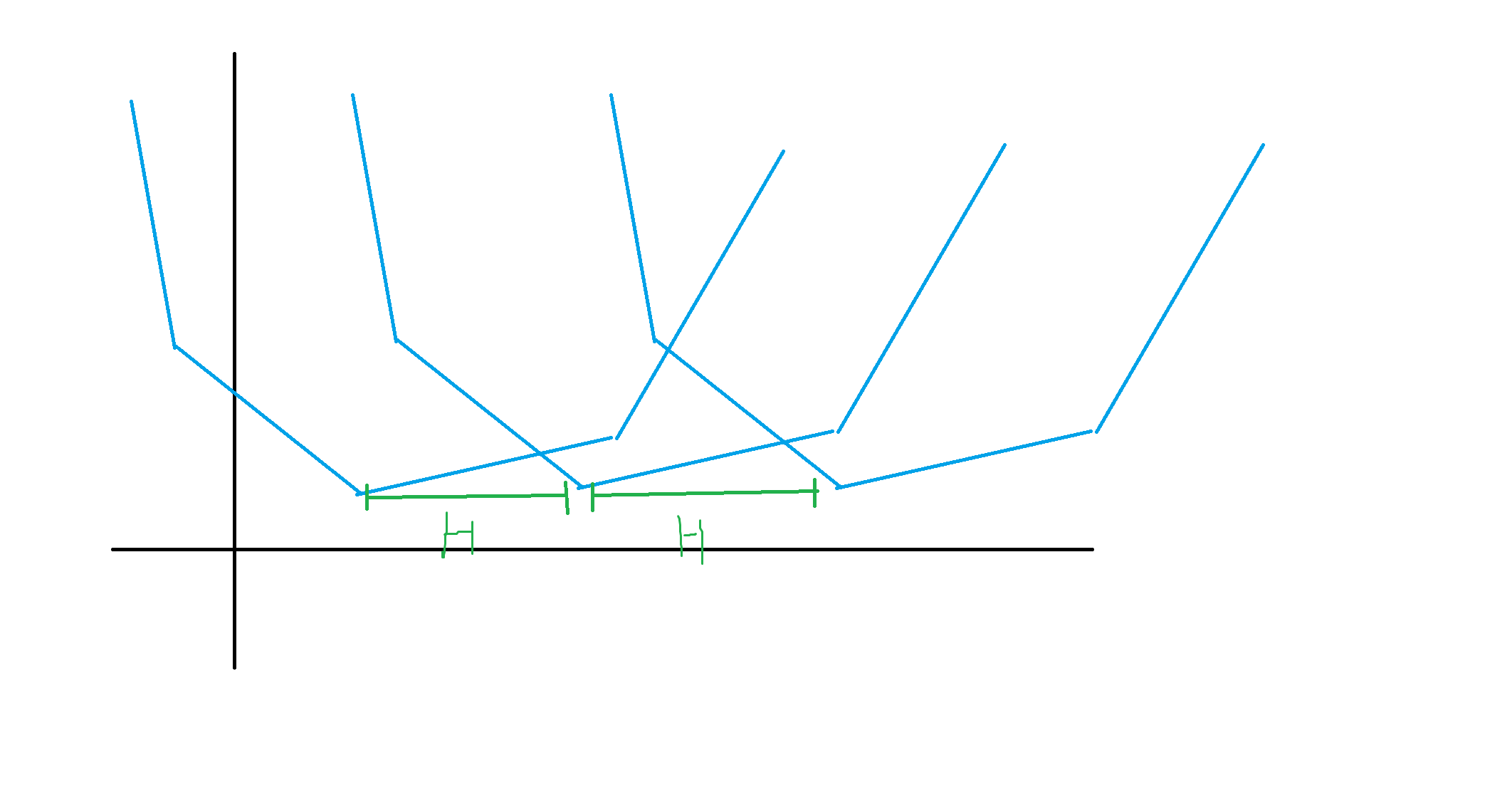
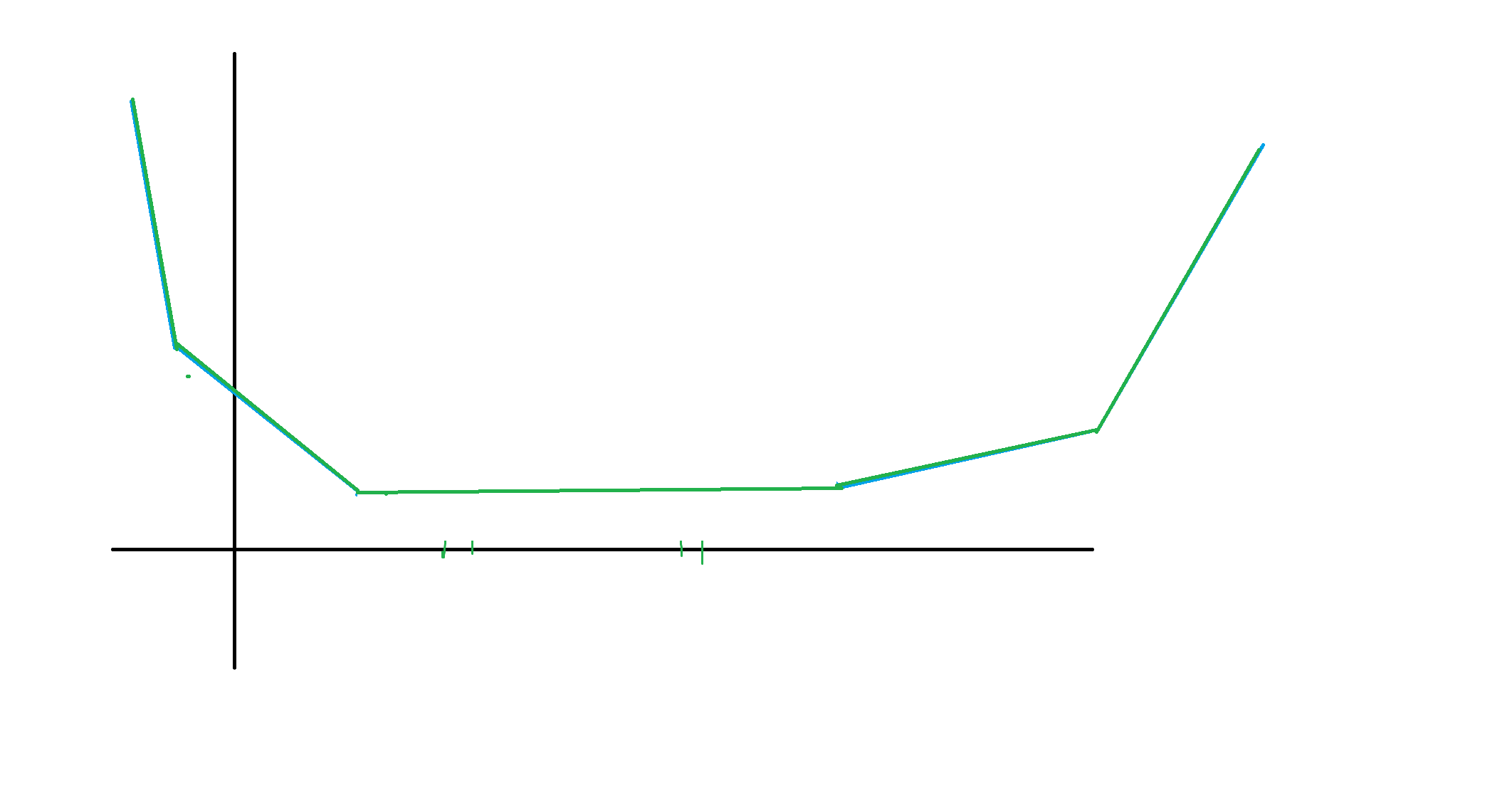
接着考虑在图 3 的基础上加入一个绝对值函数。

\[图4 \]

因为涉及到两个集合，这时需要分类讨论绝对值函数零点的位置。

记斜率为 \(0\) 的点的前驱斜率改变点和后继斜率改变点分别为 \(L\) 和 \(R\)。代码中就是左侧集合的末尾和右侧集合的开头。

• 如图 4 橙色段，如果零点 \(x_2\) 满足 \(L \leq x_2 \leq R\)：

  则斜率为 \(0\) 的点 \(x_2\) 该是 \(0\) 就是 \(0\)，答案（全局最小值）显然不变。

  只需要给左右集合各自加入一个 \(x_2\)（因为左边斜率 \(-1\)，右边斜率 \(+1\)，集合分界点就是 \(x_2\)）

• 如图 4 红色段，如果零点 \(x_1\) 满足 \(x_1 \lt L\)：

  则 \(x_1\) 左侧斜率 \(-1\)，右侧斜率 \(+1\)。

  这会导致以 \(L\) 为右端点的斜率段就会“翘起来”，分割点会到 \(L\)。

  于是在给左集合加入 2 个 \(x_1\) 的同时，还要把左集合的 \(L\) 移动到右侧集合。

  \(L\) 在改变前就对应最小值，现在离 \(x_1\) 最近，依旧对应最小值。于是维护的全局最小值 \(ans\) 要 \(+(L-x_1)\)。

• 如图 4 黄色段，如果零点 \(x_3\) 满足 \(x_3 \gt R\)：

  和第二种情况类似，这一次将 \(R\) 移动到左侧集合，\(ans \leftarrow ans + x_3-R\)。

核心代码：

#define int ll
const int N = 2e5 + 5;
int n, h;
int s[N];
multiset<int> L, R;
int tagl, tagr;
int ans = 0;
signed main(){
    n = read(), h = read();
    rep(i, 1, n) s[i] = read();
    L.insert(s[1] - tagl), R.insert(s[1] - tagr);
    rep(i, 2, n){
        tagl -= h, tagr += h;
        int l = *L.rbegin() + tagl;
        int r = *R.begin() + tagr;
        if(l <= s[i] && s[i] <= r){
            L.insert(s[i] - tagl);
            R.insert(s[i] - tagr);
        }else if(s[i] < l){
            ans += l - s[i];
            L.insert(s[i] - tagl);
            L.insert(s[i] - tagl);
            R.insert(*L.rbegin() + tagl - tagr);
            L.erase(L.find(*L.rbegin()));
        }else{
            ans += s[i] - r;
            R.insert(s[i] - tagr);
            R.insert(s[i] - tagr);
            L.insert(*R.begin() + tagr - tagl);
            R.erase(R.begin());
        }
    }
    write(ans);
    return 0;
}

数据结构完成整体维护

这里主要说一些不维护 dp 时就不被叫做数据结构的数据结构。
好神秘的称呼

凸包与半平面交

凸包——适用性（应用方法前置推导）

一个问题转换为凸包需要干这些事：

• 把问题方案 / 可能性刻画在一个二维平面上

• 将查询刻画成一个一次函数，转换为一次函数和点集的交点极值。

凸包——思想

求解凸包

分为以下步骤

1. 确定一个一定在凸包上的点，一般选取最靠左下角的，这个对所有点排序后轻松得到。

   然后将这些点扔进单调栈里。

2. 不断尝试加入新点 X：

   记录当前单调栈栈顶第 1 和第 2 分别是 \(T_1\) 和 \(T_2\)。

   如果 \(\overrightarrow{T_2T_1} \times \overrightarrow{T_1X} \gt 0\)：

   则将 \(X\) 放进单调栈；

   否则意味着 \(T_1\) 被“架空”，弹出 \(T_1\) 重复以上操作。

什么是向量叉积：

这本来是一个三维向量的概念，但是拓展到二维向量中：

设向量 \(\overrightarrow{a} = (a_x,a_y),\overrightarrow{b} = (b_x,b_y)\)。

\[\overrightarrow{a} \times \overrightarrow{b} = a_x \times b_y - a_y \times b_x \]

几何意义上：向量的叉乘表示两个向量形成的平行四边形面积，正负表示方向。

对于两个向量来说：

• \(\overrightarrow{a} \times \overrightarrow{b} \gt 0 \Leftrightarrow \overrightarrow{a}\) 在 \(\overrightarrow{b}\) 的逆时针方向上。

• \(\overrightarrow{a} \times \overrightarrow{b} \lt 0 \Leftrightarrow \overrightarrow{a}\) 在 \(\overrightarrow{b}\) 的顺时针方向上。

• \(\overrightarrow{a} \times \overrightarrow{b} = 0 \Leftrightarrow \overrightarrow{a}\) 和 \(\overrightarrow{b}\) 在一条直线上。

怎么用？

考虑求解这个问题时：有一个点集和一条只给定斜率的直线，问直线与点集交点的所有可能中，直线的（某个信息，一般是 \(Y\) 轴截距）极值？

能成为极值的点一定处于点集的凸包上，这个是可以证明的（其实挺显然的）。

然后查询时可以使用三分真的吗？找到极值。

凸包——例题

首先进行数学转换：

对于 \(A_{i,j} \le a\)，则给答案增加 \(\frac {K_i} {12}\)，这是因为 \(P(第i个人摇到A_{i,j}且硬币翻到a)=\frac 1 {12}\)。
对于 \(A_{i,j} \le b\)，则给答案增加 \(\frac {K_i} {12}\)。

发现数组 \(A\) 和 \(K\) 都是已知的，可是 \(a,b\) 未知，则将条件调换成约束 \(a,b\) 的条件：

再把 \(a,b\) 分别作为横坐标和纵坐标画成坐标系：

那么这些东西变成：

给平面上一条垂直于 \(X\) 轴的直线右侧都加一个值；
给平面上一条垂直于 \(Y\) 轴的直线上侧都加一个值；

还有一个初始的 \(-ab\)。

因为在二维平面上，所以去想扫描线。

我们扫描线枚举 \(a\)，移动时：

初始 \(-ab\) 相当于给全局加上一个斜率为 \(-1\) 的直线；
直线上方加常数这个东西不会随着扫描线移动而改变；
直线右方加常数这个东西相当于扫描线全局加常数。

那么后两个对于我们查询全局 \(\max\) 显然没有啥贡献。

问题转换为：

有一个数组，支持全局 \(a_i \leftarrow a_i - i\)，查询全局 \(\max\)。

发现可以联想到斜率为 \(-k\) 的直线，其中 \(k\) 表示操作次数。
于是扔到二维平面。
每个点 \((i,a_i)\)，相当于拿一个斜率为 \(k\) 的直线去交这个点集，直线的 \(Y\) 截距就是 \(a_i - i \times k\)，求截距的 \(\max\)。

维护凸包即可。

半平面交

半平面即一个直线的一侧，半平面交问题形如：

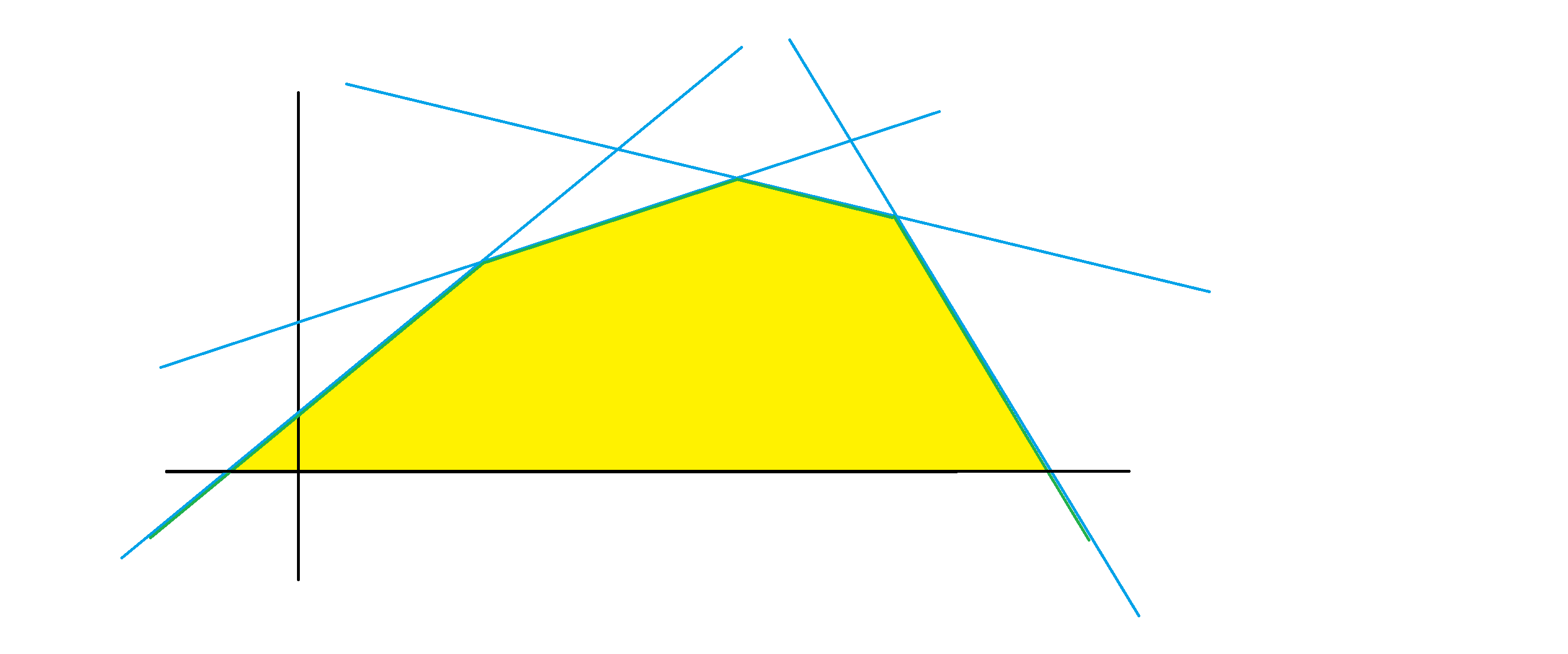
黄色部分是蓝色直线下方这一些半平面的半平面交。

其数学意义是：一堆一次函数 \(f_i(x)=k_ix+b_i\)，求 \(g(x)=\min f_i(x)\)。

这个问题当然可以计算几何爆算，但这里主要讨论如何转换为凸包。

考虑分析两个函数之间更优的条件是什么，以此拓展到全局。

\[f_1(x)=k_1x+b_1 \lt f_2(x)=k_2x+b_2 \Leftrightarrow \begin{cases} -x \lt \frac {b_2 - b_1} {k_2 - k_1}, & \text{if } k_1 \lt k_2 \\ -x \gt \frac {b_2 - b_1} {k_2 - k_1}, & \text{if } k_1 \gt k_2 \end{cases} \]

发现后面的东西很像两点之间斜率式，于是想到二维平面：每个点 \((k_i,b_i)\)。

所以半平面交和凸包其实是等价的，这也是为什么会把两者放在一个标题中。

双向单调队列

还是我自己取的名字，就是一个单调队列支持 l++、r++、r--。

用两个单调栈维护，从中间分界。

两个单调栈都不空的时候是简单的，考虑空了咋办，答案是直接重构，把分界点改成新的中心。

重构的次数是 \(O(\log n)\) 的，复杂度正确。

颜色段均摊

打脸了，我自己认为这个东西就是数据结构。（也可能是因为东西多吧，lxl 太有实力了）

直接上例题 [ABC262Ex] Max Limited Sequence

限制是要求一些区间的区间 \(\max\) 是多少。

\(\max_{i=l} ^ r a_i = x\) 可以拆开：

\[\max_{i = l} ^ r a_i \le x \land \exists i_0 \in [l,r] a_i = x \]

说人话：就是区间所有制都小于这个最大，然后因为最大是它，所有得有一个是这个值。

对于第一部分：所有值都小于某个数，求出所有数的上线 \(u_i\)。

• 扫描线，扫描下标，一个堆维护覆盖该位置的区间集合。

  在每个区间 \(l\) 处加入，\(r+1\) 处删除，可以延迟删除。

• 直接线段树，暴力美学！！！！！

对于第二部分：一个区间存在一个特定值。

计数问题要考虑限制之间的影响情况，于是分析限制之间会不会影响。

当前限制为 \([l,r]\) 区间存在 \(x\)，如果一些已经 \(\lt x\)，显然不能。而且所有位置都是 \(\le x\) 的，所有不影响。

于是根据 \(P(AB)=P(A)P(B)，事件A和B独立\)。（又在装）

算出所有限制的方案数后连乘即可。

问题就是找出一个区间中有一个特定值 \(x\) 的方案。

这种问题显然是 dp 吧，不要多想，先去想最暴力的。

\(dp_{i,j}\) 表示填完了前 \(i\) 个位置，最后一个 \(=x\) 的数下标为 \(j\)。

转移平凡：

• \(dp_{i-1,j} \rightarrow dp_{i,i}\)

• \(dp_{i-1,j} \times x \rightarrow dp_{i,j}\)

• 对于限制 \([l,i]\) 清空 \(dp_{i,j},j \lt l\)。

往数据结构上套下看看，发现是：

• 单点赋值全局和

• 全局乘

• 前缀清空

线段树当然可以，但是可以维护相同值的区间。

“提一下这个维护相邻相同数，由于某些人比较...呃...由于某些人比较...比较毒瘤，所以 OI 中出现了一些奇奇怪怪的算法”

于是可以上 ODT，剩下的不说了，应该在数据结构专题里说。