搜索——前 k 小问题

增量法：

例题：

一个一般的前 k 小问题。两个序列各自选择一个数，问和的第 k 小可能是多少。

将两个序列分别排序，各自选择第一个，显然这种是全局最小。考虑用这种状态作为初始状态进行拓展。

每次可以将一个序列选择数的下标 + 1，去重后放入优先队列。显然优先队列的第 k 个取出的即为答案。

例题2：

当所求的是三个序列时怎么做？

就是将原来的二维搜索树转换在三维空间。

考虑如何去重，发现每个点 \((i,j,k)\) 都可能从 3 个地方来。分别是 \((i-1,j,k)\)，\((i,j-1,k)\) 和 \((i,j,k - 1)\)

可以限制每个方案的拓展，让每个方案只从一个状态来。

如：

• 只有 \(j=1\) 且 \(k=1\) 是拓展到 \((i+1,j,k)\)
• 只有 \(k=1\) 时拓展到 \((i,j+1,k)\)
• 随意拓展到 \((i,j,k+1)\)

时间复杂度 \(O(n\log n+k\log k)\)

总结1

前 k 小问题

我们要找到一个搜索的扩展顺序满足：

• 1. 每个状态都能扩展到
• 2. 每个状态扩展的状态都 \(\geq\) 自己

有这两点就有一个基本算法：

用一个优先队列维护所有待扩展状态。

【每次从优先队列取出最小的。】

（如果这个状态之前已经访问过的就直接跳过）

扩展取出的状态，都放进优先队列。

这个算法总是按从小到大的顺序取出所有状态的。

问题：

• 1. 去重很麻烦
• 2. 记录整个状态很麻烦（因为要 \(O(n)\)）
• 3. 一个状态直接后继太多很麻烦

于是每个状态有一定要求：

• 1. 每个状态都能扩展到
• 2. 每个状态扩展的状态都 \(\geq\) 自己
• 3. 每个状态的后继不多
• 4. 每个状态扩展出来的方式是唯一的
• 5. 只记录需要记录的信息

应用（tricks）

例题1

给一个序列，序列中选出若干个数字求和，问第 \(k\) 小的和。数据范围 \(n,k \leq 10^3\)

如果套用增量法，排序后，每次找编号更大的。但是这样可能在优先队列里扔进去 \(O(nk)\) 个元素，时间复杂度还是 \(O(nk)\)。

还是考虑排序后，这一次我们限制只能加入编号大 \(1\) 的元素。

为了让所有状态都能拓展到，另外允许将方案的最后一个数向后挪一位，即删除最大值加入后面第一个。

这样后继状态是 \(O(1)\) 的了。

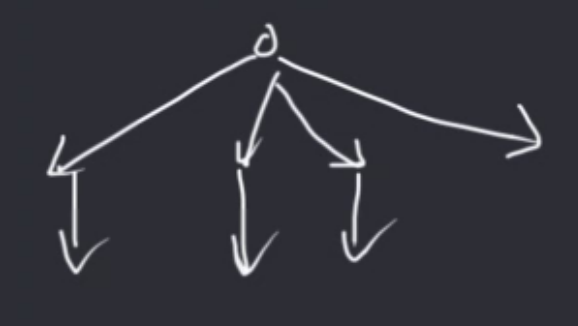
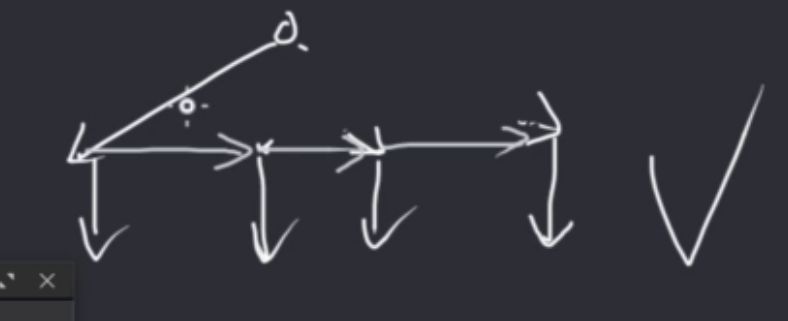
如果从搜索树的角度看，就是试图优化一个出度很大的节点。

这种方法可以概括为 孩子-兄弟表示法，附上 LCA 画的简图。

例题2（源自思考题5）

有 \(n\) 个整数，请你求出所有大小恰好为 \(m\) 的子集中，前 \(k\) 小的子集和。

对例题 1 的做法举一反三。

初始状态显然是排序后选择前 \(m\) 个数字。

两种拓展方式

• 将最后一段排名连续的数字一起往后挪。
• 对于最后一段排名连续的数字，把他们的第一个留下，分割开后将剩余的一坨往后挪。

例题3 （源自思考题6）P2541 [USACO16DEC] Robotic Cow Herd P

题意：有 \(n\) 个数列，每个数列长为 \(m\)，问每个数列中各选一个数的所有方案中，前 \(k\) 小的和分别是多少。

这个题就是考虑每个数列选择数的下标组成的新序列 \(a[1...n]\)，每个长度为 \(m\) 的序列都假设为 0-index。

以下是 3 种拓展方式

• 把 \(a_1,a_2,...,a_p,a_{p+1},...,a_n\) 变为 \(a_1,a_2,...,a_p+1,a{p+1},...,a_n\)。即将当前数列往后选一个。
• 把 \(a_1,a_2,...,a_p,a_{p+1},...,a_n\) 变为 \(a_1,a_2,...,a_p,a_{p+1}+1,...,a_n\)。即当前数列定下来，把下一个数列往后选一个。
• 把 \(a_1,a_2,...,a_p=1,a_{p+1},...,a_n\) 变为 \(a_1,a_2,...,0,a_{p+1}+1,...,a_n\)。当前序列选择若是 1，则反悔掉，撤销成 \(0\)。