ACK-Ackermann, 阿克曼函数
以前好几次在学语言的使用都有实现这个ack函数的经历,今天读本算法书,偶尔又提到了这个,查了下wiki来头好大
| m\n | 0 | 1 | 2 | 3 | 4 | n |
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 |  |
| 1 | 2 | 3 | 4 | 5 | 6 | 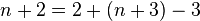 |
| 2 | 3 | 5 | 7 | 9 | 11 | 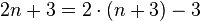 |
| 3 | 5 | 13 | 29 | 61 | 125 |  |
| 4 | 13 =  |
65533 =  |
265536 − 3 =  |
 =  |
 =  |
 |
以前好几次在学语言的使用都有实现这个ack函数的经历,今天读本算法书,偶尔又提到了这个,查了下wiki来头好大
| m\n | 0 | 1 | 2 | 3 | 4 | n |
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 |  |
| 1 | 2 | 3 | 4 | 5 | 6 | 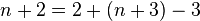 |
| 2 | 3 | 5 | 7 | 9 | 11 | 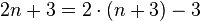 |
| 3 | 5 | 13 | 29 | 61 | 125 |  |
| 4 | 13 =  |
65533 =  |
265536 − 3 =  |
 =  |
 =  |
 |
