动态规划

内容概要

　　一、什么是动态规划

　　二、动态规划实例，斐波那契数列

　　三、钢条切割问题

　　四、最长公共子序列

 

1、动态规划

　　动态规划不是一种特定的算法，而是一种算法思想，是一种解决问题的方法

　　动态规划一般用于求解最优解问题

　　如何发现并判断那些问题能够运用动态规划思想，并且找到问题的递推式是关键

 

2、斐波那契数列

　　斐波那契数列是一种特殊的数列，它满足第一和第二项均为1，后面的项等于它的前两个项的和

　　比如[1, 1, 2, 3, 5, 8, 13......]就是斐波那契函数

 

　　想在需要完成一个函数，它能返回斐波那契函数第n项的值

　　　　使用递归完成

#include <stdio.h>

int feibonaqi(int n);

int feibonaqi(int n){
    if (n == 1 || n == 2){
        return 1;
    }
    else{
        return feibonaqi(n-1) + feibonaqi(n-2);
    }
}


int main(void){
    int n = 0, res = 0;
    printf("please input a number:");
    scanf("%d", &n);
    res = feibonaqi(n);
    printf("No.%d:  %d", n, res);    
    return 0;
}

　　　　使用递归发现可以完成任务，比如输入6，它会正确地返回8；但是，如果你输入100，那么即使是c语言，小程序也卡住了，因为它要计算的量太大了

　　　　导致递归效率慢有很多原因，比如新开栈空间需要时间，更重要的原因是因为重复计算子问题

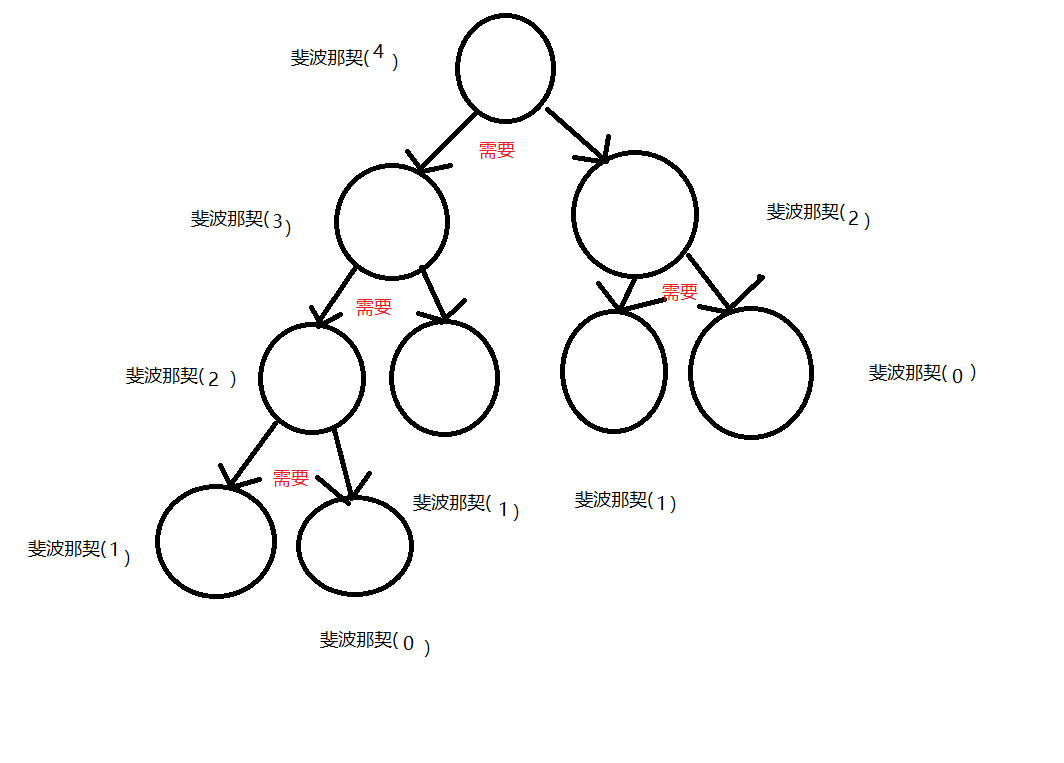
　　　　会发现，计算斐波那契(4),斐波那契(2)重复计算2次,斐波那契(1)重复计算3次。这样的递归算法时间复杂度为O(n**2)

 

　　使用非递归，自下而上计算，并且把计算过的值记录下来，就可以避免重复计算了

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

int *feibonaqie(int **p, int n);
void traverse(int *p, int n);

int *feibonaqie(int **p, int n){  // 创建斐波那契数列
    if (n==1 || n==2){
        *p = (int *)malloc(n*4);
        for (int i = 0; i<n; i++){
            *(*p+i)=1;
        }
        return *p;
    }
    else if (n > 2){
        *p = (int *)malloc(n*4);
        **p = 1;
        *(*p+1) = 1;
        for (int i = 2; i<n; i++){
            *(*p+i) = *(*p+i-1) + *(*p+i-2);
        }
        return *p;
    }
    else{
        return NULL;
    }
}

void traverse(int *p, int n){  //用于遍历的方法
    for (int i=0; i<n; i++){
        printf("%d,", *(p+i));
    }
}


int main(void){
    int n = 0;
    printf("please input length:");
    scanf("%d", &n);
    int *p = NULL;
    
    p = feibonaqie(&p, n);
    traverse(p, n);
    return 0;
}

　　斐波那契梳理的递推式

　　f(n) = f(n-1) + f(n-2) , n>=2;

　　      = 1, n<2;

 

3、钢条切割问题

　　现有一根长度为n的钢条，现在需要知道怎么切割钢条赚钱的利益最大

　　以下是钢条长度与售价的表格

　　　　假如现在有一条长度为4的钢条，那么怎么切割，或者不切割，赚取的钱最多

　　　　长度为4的钢条的所有切割方案共有8种

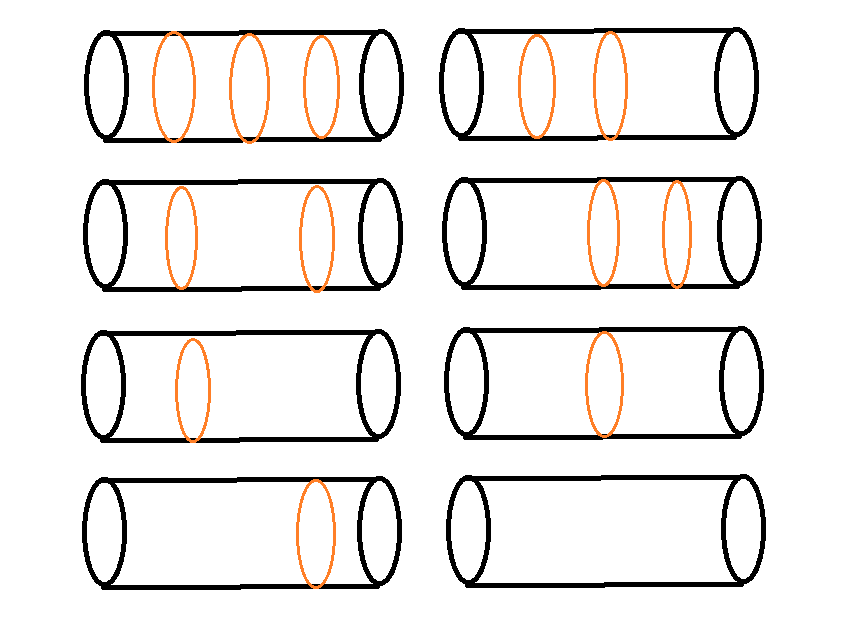
　　　　长度为4的钢条只有8种切割方案，但是如果长度为64呢？

　　　　由于长度为n的钢条共有n-1个可切割的位置，这些位置又可以选择不切或者切，所以对于长度为n的钢条，所有切割方案有2**(n-1)种，如果暴力枚举所有情况，非常大。

 

　　问题解决思路

　　　　由于数据不大，可以通过直接观察，长度为4的钢条最优切割方案为切成2段长度为2的钢条

 

　　　　对于长度为4的钢条

　　　　　　如果只切一刀，切成1和3两段，1无法继续切割，3可以继续切割。

　　　　　　原本应该讨论是否继续切割3的钢条，但如果已经知道长度为3的钢条最多能卖多少钱，就不需要讨论怎么切了，因为无论怎么切，最多能卖的钱是不变的

　　　　　　于是我们将问题由长度为4的钢条怎么切割转向为长度为3的钢条怎么切割

　　　　同理，要求长度为3的钢条的最优解，我们需要知道长度为2的钢条的最优解

　　　　　　还有一种情况，那就是切成2和2两段，那么同样需要知道2的最优解

　　　　　　最后，只要比较一下两种切割方案和不切割方案谁最大就可以了

 

　　　　但是上面只是切了一刀，如果切很多刀？

　　　　其实，只切一刀，对切完后的两段取最优解，此时已经隐含地切了，只是不知道具体的切法

 

　　　　以下是最优解和其切法

　　　　　　

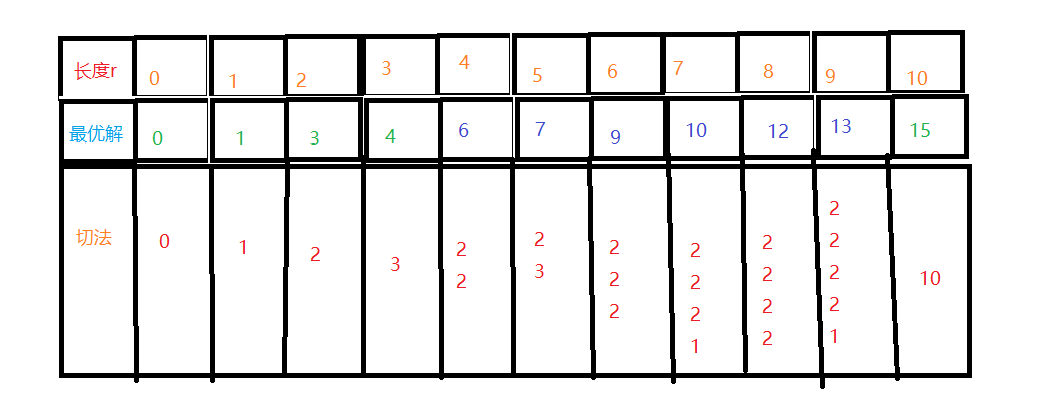
　　　　　　就拿6做例子，6的最优切法为2，2，2

　　　　　　如果只切一刀，切成2和4，那么2这一段最有切法为不切；另一端4的最优切法为2，2。采用4的最优解的同时，其实已经隐含地切采用了最优的切法

#include <stdio.h>
#include <time.h>

typedef int (*func)(int *, int);

int time_dec(func, int *, int);
int iron_cut_rec(int *p, int n);  //两段都采用最优解，递归
int iron_cut_rec2(int *p, int n);  //只有一段采用最优解，另一端不切，递归
int iron_cut_no_rec(int *p, int n);  //非递归

int time_dec(func f, int *p, int n){
    time_t t1, t2;
    t1 = time(NULL);
    int res = (*f)(p, n);
    t2 = time(NULL);
    printf("%.8f\n", t2-t1);
    return res;
}
int iron_cut_rec(int *p, int n){
    int res1 = *(p+n);
    for (int i=1; i<n; i++){
        int res = iron_cut_rec(p, n-i)+iron_cut_rec(p, i);
        if (res > res1){
            res1 = res;
        }
    }
    return res1;
}
int iron_cut_rec2(int *p, int n){
    int max = *(p+n);
    for (int i=1; i<n; i++){
        int res = *(p+i) + iron_cut_rec2(p, n-i);
        if (max < res){
            max = res;
        }
    }
    return max;
}
int iron_cut_no_rec(int *p, int n){
    int res[n+1] = {0};
    for (int i=1; i<n+1; i++){
        int max = *(p+i);
        for (int j=1; j<i; j++){
            int new_n = res[j] + res[i-j];
            if (max < new_n){
                max = new_n;
            }
        }
            res[i] = max;
    }
    return res[n];
}

int main(void){
    int price_table[11] = {0, 1, 3, 4, 5, 6, 8, 9, 11, 12, 15};
    int m = 0;
    scanf("%d", &m);
    printf("%d \n",time_dec(&iron_cut_rec, price_table, m));
    printf("%d \n",time_dec(&iron_cut_rec2, price_table, m));
    printf("%d \n",time_dec(&iron_cut_no_rec, price_table, m));
    return 0;
}

　　　第二个函数里，理解为什么一段可以不切割，另一端采用最优解，也能解决问题，并且效率更高起来挺困难的。

 

4、最长公共子序列

　　偷懒了，忘了重新看视频吧

 

#include <stdio.h>
#include <string.h>

int similar(char *p, char *c){
    int x, y, i, j;
    x = strlen(p) + 1;
    y = strlen(c) + 1;
    int a[x][y] = {0};
    
    for (i=0; i<x; i++){
        for (j=0; j<y; j++){
            a[i][j] = 0;
            printf("%d,", a[i][j]);
        }
        printf("\n");
    }
    printf("\n");
    
    for (i = 0; i<x-1; i++){
        for (j = 0; j<y-1; j++){
            if (*(p+i) == *(c+j)){
                a[i+1][j+1] = a[i][j] + 1;
            }
            else{
                if (a[i+1][j] > a[i][j+1]){
                    a[i+1][j+1] = a[i+1][j];
                }
                else{
                    a[i+1][j+1] = a[i][j+1];
                }
            }
        }
    }

    for (i=0; i<x; i++){
        for (j=0; j<y; j++){
            printf("%d,", a[i][j]);
        }
        printf("\n");
    }

    i = x-1;
    j = y-1;
    while(a[i][j] != 0){
        if (a[i][j] == a[i][j-1]){
            j-=1;
        }
        else if (a[i][j] == a[i-1][j]){
            i-=1;
        }
        else{
            printf("%c", *(p+i-1));
            i-=1;
            j-=1;
        }
    }
    return 222;
}

int main(void){
//    char a[] = "hello world";
//    char *p = a;
//    printf("%d, %d\n", sizeof(a), strlen(a));
//    printf("%d, %d\n", sizeof(p), strlen(p));

    char a[] = "aefaega";
    char b[] = "aegsdgg";
    similar(a, b);
    return 0;
}