非线性数据结构——树

内容概要

　　一、树数据结构的实例——模拟文件系统

　　二、二叉树再接触——二叉树的遍历

　　三、二叉树再接触——二叉搜索树的应用

　　四、二叉搜索树偏斜问题，复杂度

　　五、偏斜问题解决，AVL树

 

1、树数据结构的实例——模拟文件系统

class FolderSystem:
    class Node:
        def __init__(self, name, type='dir'):
            self.name = name
            self.type = type
            if type == 'dir':
                self.child = []
                self.parent = None

    def __init__(self):
        self.root = self.Node('/')  # 创建根目录
        self.current = self.root  # 记录当前目录名

    def mkdir(self, name):
        for obj in self.current.child:
            if obj.name == name and obj.type == 'dir':
                print("您要创建的文件名在当前目录下已存在!")
                return

        new_dir = self.Node(name)
        self.current.child.append(new_dir)
        new_dir.parent = self.current

    def touch(self, name):
        for obj in self.current.child:
            if obj.name == name and obj.type == 'file':
                print("您要创建的文件在当前目录下已存在!")
                return

        new_file = self.Node(name, 'file')
        self.current.child.append(new_file)

    def ls(self):
        for obj in self.current.child:
            print(obj.name, end=',')

    def cd(self, path):
        tmp = self.current
        #相对路径
        if path.startswith('./'):
            path = path.lstrip('./')
        elif path.startswith('../'):
            path = path.lstrip('../')
            self.current = self.current.parent
            if not self.current:
                self.current = tmp
                print("目前所在的文件夹为根目录!")
                return
        #绝对路径
        elif path.startswith('/'):
            path = path.lstrip('/')
            self.current = self.root

        per_name_li = path.split('/')
        for name in per_name_li:
            if not self.current.child:  # 判断当前文件夹是否不为空
                for obj in self.current.child:
                    if obj.name == name and obj.type == 'dir':  # 找到当前文件夹下是否有对应文件夹名
                        self.current = obj
                        break
                else:
                    self.current = tmp
                    print("文件名不存在!")
                    break
            else:
                self.current = tmp
                print("后续文件夹为空")
                break

    def rm(self, mode=''):
        ...

 

2、二叉树的遍历

　　二叉树有两种实现方式

　　　　一种是线性组织方式，比如之前的堆排序中，就是使用的列表存储的堆

　　　　但是这种方式只适合存储完全二叉树，如果为非完全二叉树，列表存储的值是不连续的

 

　　　　另一种方式是链式存储方式，这种方式类似链表，它存有下一个节点的地址

　　　　这种方式允许存储非完全二叉树

class BiTreeNode:
    def __init__(self, data=None):
        self.data = data
        self.lchild = None
        self.rchild = None
        self.parent = None


a = BiTreeNode('A')
b = BiTreeNode('B')
c = BiTreeNode('C')
d = BiTreeNode('D')
e = BiTreeNode('E')
f = BiTreeNode('F')
g = BiTreeNode('G')

a.lchild = b
a.rchild = c
b.lchild = d
b.rchild = e
c.rchild = f
e.rchild = g

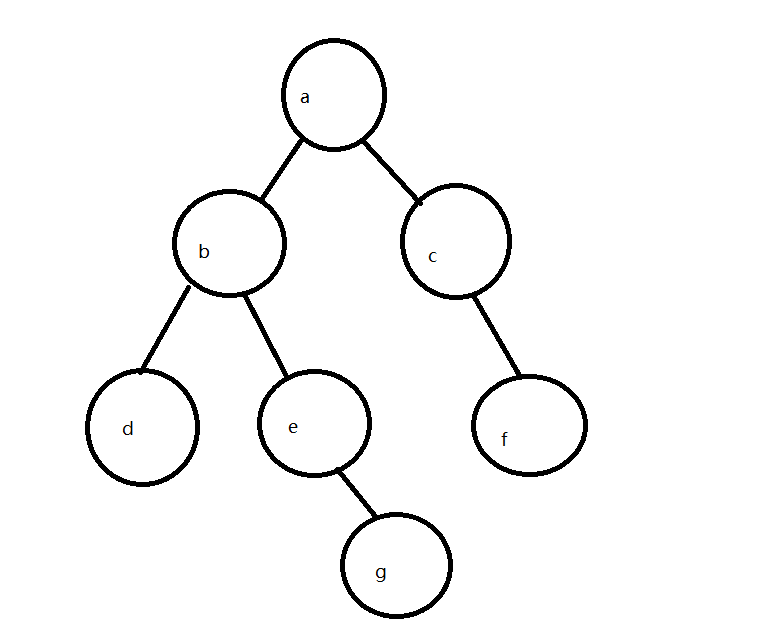
　　二叉树的三种遍历方式

　　　　-前序遍历

def pre_order(node):
    if node:
        print(node.data)
        pre_order(node.lnode)
        pre_order(node.rnode)

 　　　　前序遍历遍历的过程与快速排序的算法过程有些类似

　　　　　　快速排序是先归位一个数，在递归前一部分和后一部分

　　　　　　而前序遍历是先打印当前节点的数值，在递归调用左子树和右子树

　　　　前序遍历的结果为

　　　　　　ABDEGCF

 

　　　　-中序遍历

def in_order(node):
    if node:
        in_order(node.lnode)
        print(node.data)
        in_order(node.rnode)

　　　　中序遍历是先递归调用左子树，在打印当前数值，最后递归调用右子树

　　　　中序遍历的结果为 DBEGACF

 

　　　　-后序遍历

def af_order(node):
    if node:
        af_order(node.lnode)
        af_order(node.rnode)
        print(node.data)

　　　　后序遍历与归并排序算法相似，归并排序先递归将前部分数组和后半部分数组变为有序，在进行最后的一次归并

　　　　　　后序遍历先递归调用左子树和右子树，在打印当前节点数值

　　　　　　后序遍历的结果为 DGEBFCA

 

　　　　特别需要注意的是：在知道一个二叉树的前序遍历、后序遍历和中序遍历中的任意两个时，就能反推出这个二叉树的结构

 

　　　　-层次遍历

　　　　　　层次遍历就是根据树的深度从左到右打印每一层节点的数值

　　　　　　层次遍历的结果为ABCDEFG

　　　　**这个递归的层次遍历是错误的**

def level_order(node):
    from collections import deque
    dq = deque([node])

    def _level_order(queue):
        node = queue.popleft()
        if node:
            print(node.data, end=',')
            dq.append(node.lchild)
            dq.append(node.rchild)
            _level_order(dq)

    _level_order(dq)

　　　　层次遍历迭代方式的写法

def level_order(node):
    from collections import deque
    dq = deque([node])
    while len(dq) > 0:
        node = dq.popleft()
        if node:
            print(node.data, end=',')
            dq.append(node.lchild)
            dq.append(node.rchild)

 

3、二叉搜索树的应用

　　二叉搜索树其实是一种特殊的二叉树

　　与堆排序中的小根堆或者大根堆类似，小根堆和大根堆是关于父节点和孩子节点间的关系（孩子节点总比父节点大或者小）

 

　　而二叉搜索树的父亲节点总比左子树的任何节点大，而比右孩子树的任何节点小

　　这样的结构使得使用二叉搜索树搜索时有些类似二分搜索

 

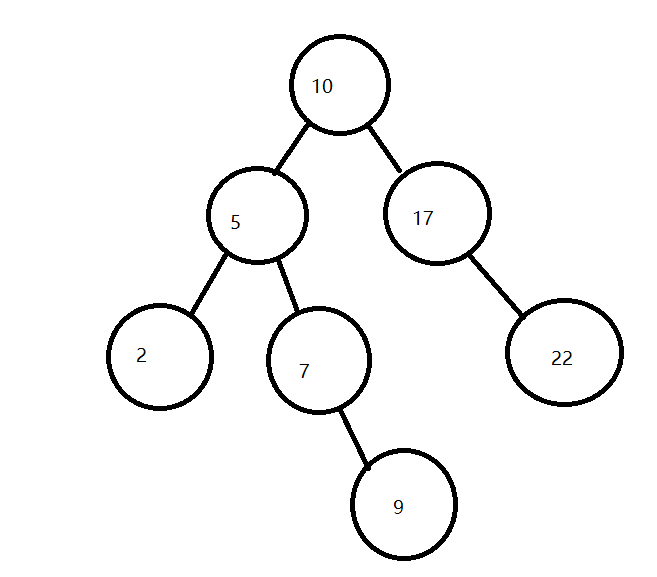
　　二叉搜索树的插入、搜索

class BiTree:
    class BiTreeNode:
        def __init__(self, data):
            self.data = data
            # self.count = count  # count在__init__初始化函数中设置为默认形参，默认值为0，用于统计相同的值出现的次数
            self.lchild = None
            self.rchild = None
            self.parent = None

    class BiTreeIterator:
        def __init__(self, head):
            self.head = head
            self.stack = [self.head]

        def __iter__(self):
            return self

        def __next__(self):
            if len(self.stack):
                node = self.stack.pop()
                if node.rchild:
                    self.stack.append(node.rchild)
                if node.lchild:
                    self.stack.append(node.lchild)
                return node.data
            else:
                raise StopIteration

    def __init__(self, data):
        self.root = self.BiTreeNode(data)

    def insert(self, data):
        node = self.root
        while 1:
            if data > node.data:
                if not node.rchild:
                    node.rchild = self.BiTreeNode(data)
                    break
                else:
                    node = node.rchild
            elif data < node.data:
                if not node.lchild:
                    node.lchild = self.BiTreeNode(data)
                    break
                else:
                    node = node.lchild

    def search(self, data):
        node = self.root
        while node:
            if data > node.data:
                node = node.rchild
            elif data < node.data:
                node = node.lchild
            else:
                print("找到了!")
                return 1
        else:
            print("你要找的数不存在!")

    def delete(self, data):
        node = self.root
        parent = None
        connect = ''

        while node:
            if data > node.data:
                parent = node
                node = node.rchild
                connect = 'l'
            elif data < node.data:
                parent = node
                node = node.lchild
                connect = 'r'
            else:
                if not (node.lchild or node.rchild):  # 要删除的节点没有子树
                    if connect == 'l':
                        parent.lchild = None
                    elif connect == 'r':
                        parent.rchild = None
                    else:
                        print("当前只有根节点，不能删除!")

                elif node.lchild and node.rchild:  # 要删除的节点左右子树都有
                    # 默认交换左子树中最大的节点
                    ech_node = node.lchild
                    ech_parent = None
                    while ech_node.rchild:
                        ech_parent = ech_node
                        ech_node = ech_node.rchild
                    if not ech_parent:
                        node.lchild = ech_node.lchild
                    else:
                        ech_parent.rchild = ech_node.lchild

                    # 将替换的节点与被删除的节点替换
                    if connect == 'r':
                        parent.rchild = ech_node
                    elif connect == 'l':
                        parent.lchild = ech_node
                    else:
                        self.root = ech_node

                    ech_node.rchild = node.rchild
                    ech_node.lchild = node.lchild
                    node.rchild = None
                    node.lchild = None

                else:  # 要删除的节点只有左右子树中的任意一个
                    if connect == 'l':
                        if node.lchild:
                            parent.lchild = node.lchild
                        else:
                            parent.lchild = node.rchild
                    elif connect == 'r':
                        if node.lchild:
                            parent.rchild = node.lchild
                        else:
                            parent.rchild = node.rchild
                    else:
                        if node.lchild:
                            self.root = node.lchild
                        else:
                            self.root = node.rchild

    def __iter__(self):
        return self.BiTreeIterator(self.root)


bt = BiTree(10)
bt.insert(5)
bt.insert(17)
bt.insert(2)
bt.insert(7)
bt.insert(9)
bt.insert(22)

print(bt.search(9))
print(bt.search(8))

for i in bt:
    print(i, end=',')
# 10,5,2,7,9,17,22

 

　　二叉搜索树的删除（这部分比较难）

　　　　假设要被删除的节点为A，有三种情况

　　　　　　情况一：A为叶子节点

　　　　　　　　操作：直接删除

　　　　　　情况二：A仅有左子树或是右子树

　　　　　　　　操作：将仅有的子树的根节点与A的父节点连接

　　　　　　情况三：A满足同时拥有左子树和右子树

　　　　　　　　操作：将左子树中最大的节点与被删除节点替换   或是  将右子树中最小的节点与被删除节点替换

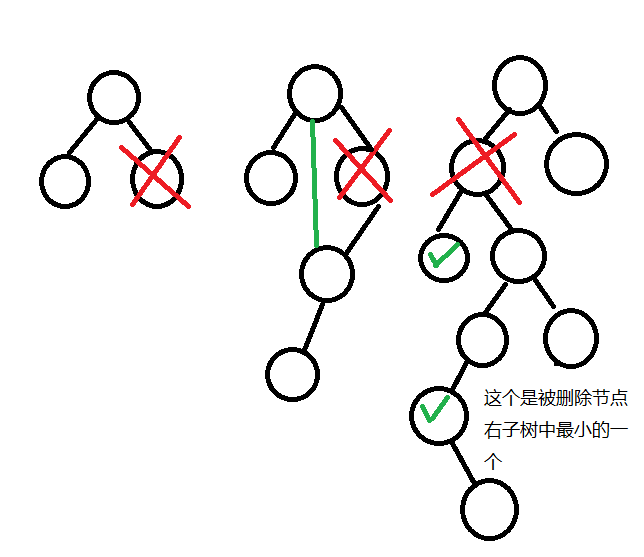
　　替换节点的情况也只有两种

　　　　情况一：被替换的节点为叶子节点

　　　　　　操作：直接替换

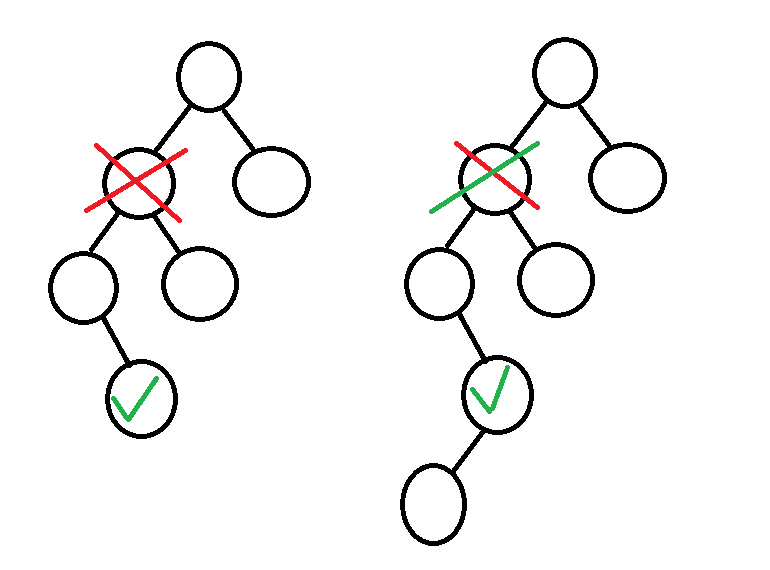
　　　　情况二：被替换的节点存在一个子树

　　　　　　操作：将子树根节点与被替换节点的父节点连接

　　　　不存在被替换节点同时拥有左右子树

4、二叉搜索树偏斜问题、复杂度

　　普通的二叉搜索树存在一个问题，类似快速排列，存在最差的情况。普通的二叉搜索树查找的平均时间复杂度为O (logn)，最坏的情况下的复杂度为O(n)

　　例如将一系列升序的数据依次存放到普通的二叉搜索树时[1,2,3,4,5,6,7,8,9]

　　这样将会得到偏斜的二叉树

 

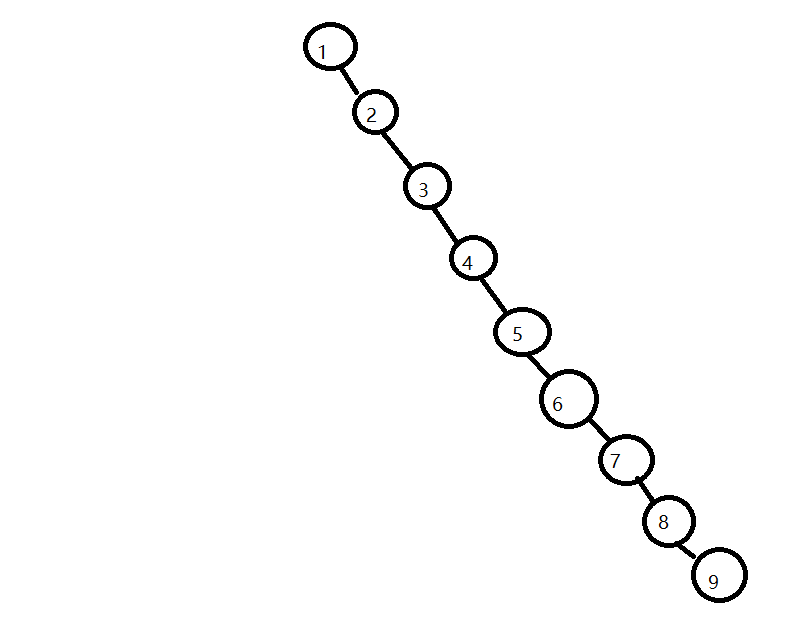
5、偏斜解决——AVL树

　　数据存放的最终目的还是为取数据，为了使取数据变得方便。所以在存放新数据的时候，要保证二叉搜索树不那么偏斜，就是AVL树了。

　　AVL树是一种自平衡树，它的左右子树都是自平衡树

　　AVL树满足它的左右子树的深度之差的绝对值小于1

 

　　于是在普通二叉搜索树的节点上增加一个属性（平衡因素），用于记录左右子树的高度差

　　　　当左子树高度比右子树小一时，这个值为-1；

　　　　当右子树高度比左子树大一时，这个值为1；

　　　　当左右子树的高度一致时，这个值为0；

 

　　插入一个新节点时有两种情况

　　　　第一种是没有破坏整个树的平衡

　　　　　　正常插入之后需要更新有关节点的平衡因素

　　　　　　平衡因素的更新——最先检测插入节点的父节点

　　　　　　　　当插入节点为左节点时，父节点平衡因素-1

　　　　　　　　当插入节点为右节点时，父节点平衡因素+1

 

　　　　　　　　当更新后的父节点平衡因素为-1时，父节点的父节点平衡因素-1

　　　　　　　　当更新后的父节点平衡因素为+1时，父节点的父节点平衡因素+1

　　　　　　　　当更新后的父节点平衡因素为0时，更新结束，不再追溯标记值的更新

　　　　　　　　否则继续回溯更新

 

　　　　第二种是破坏了树的平衡

　　　　　　与添加节点有关的节点中，由添加节点回溯，最先平衡被打破的记为K

　　　　　　下图中的10为K

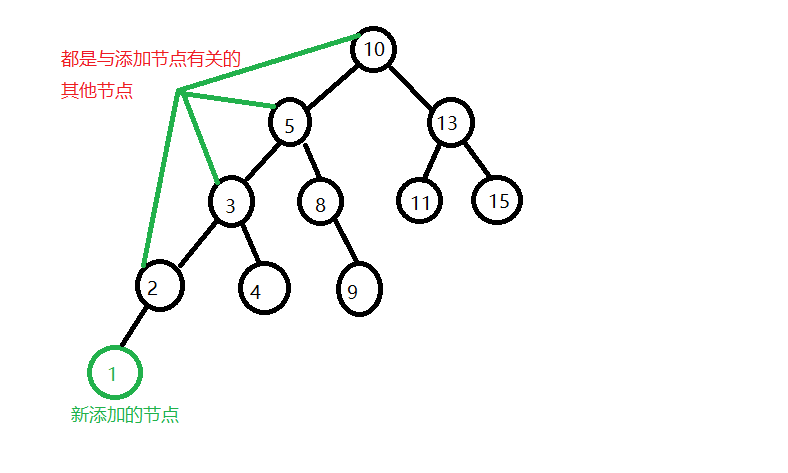
　　　　　　此时存在4种情况

　　　　　　　　不平衡是由K的右孩子的右子树插入新节点导致的

　　　　　　　　　　解决办法——左旋

 

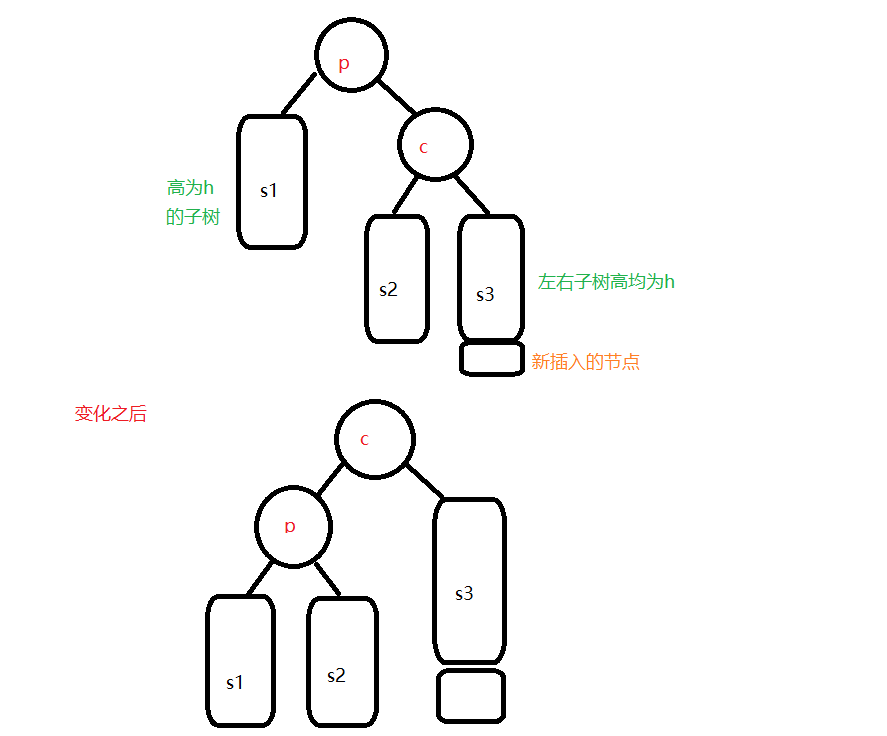
　　　　　　　　不平衡是由K的左孩子的左子树插入新节点导致的

　　　　　　　　　　解决办法——右旋

 

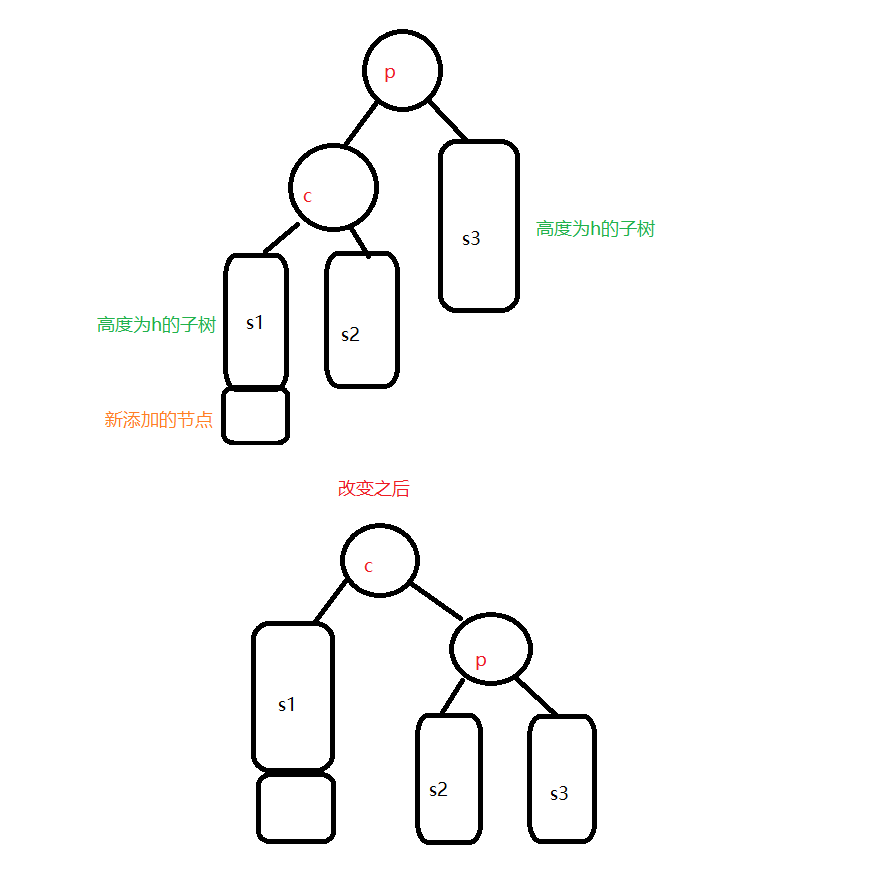
　　　　　　　　不平衡是由K的右孩子的左子树插入新节点导致的

　　　　　　　　　　解决办法——先右旋再左旋

 

 

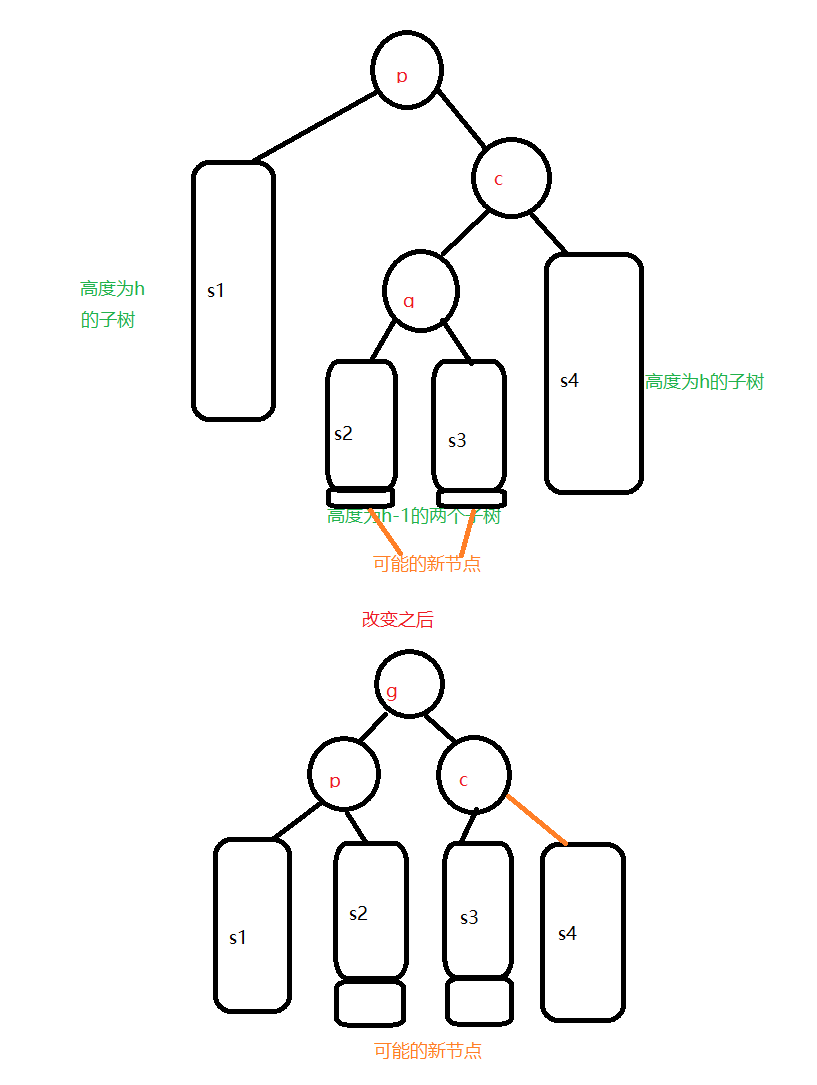
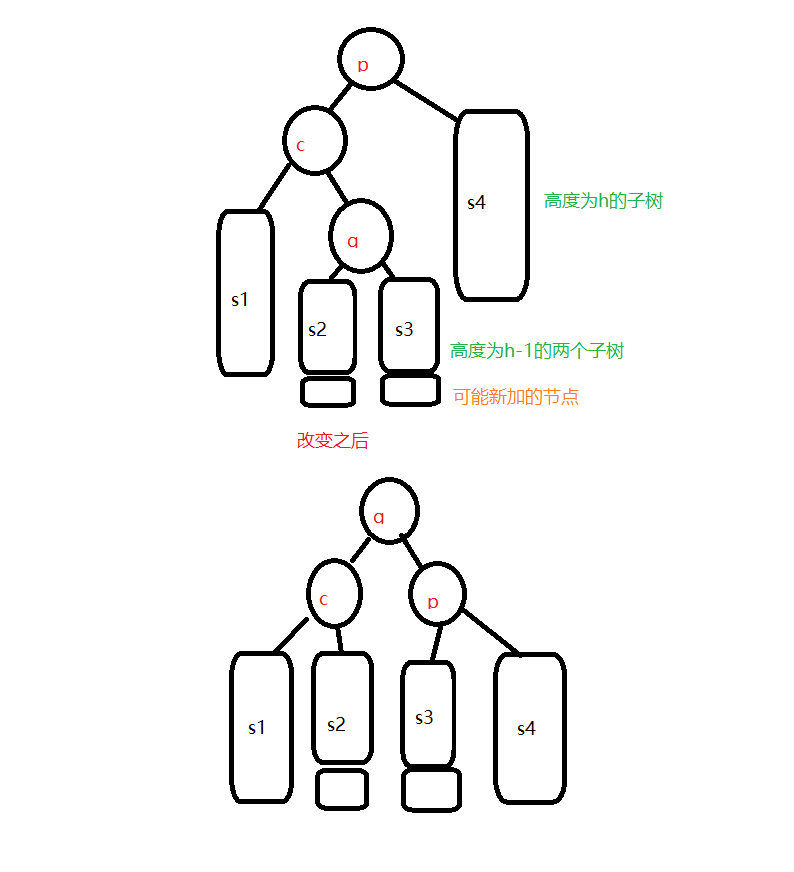
　　　　　　　　不平衡是由K的左孩子的右子树插入新节点导致的

　　　　　　　　　　解决办法——先左旋再右旋

#include <stdio.h>
#include <stdlib.h>

struct AVLTreeNode{
    int value;  // 节点存放的值
    int count;  // 节点存放相同值的数量，这里可以改成链表，类似拉链法
    int child_mark;  // 用于记录当前节点是父节点的孩子左孩子节点还是右孩子节点 1表示左孩子节点，2表示右孩子节点,0表示没有父节点
    int balance_factory;  // 平衡因素
    struct AVLTreeNode *lchild;  // 节点的左节点
    struct AVLTreeNode *rchild;  // 节点的右节点
    struct AVLTreeNode *father;  // 节点的父节点
};

typedef struct AVLTreeNode ToAVLTreeNode;

void add_node(int value, ToAVLTreeNode **root);
void flush_balance_factory(ToAVLTreeNode *node, ToAVLTreeNode **root);
void front_traverse(ToAVLTreeNode *head);  //前置遍历
void right_turn(ToAVLTreeNode *p, ToAVLTreeNode *c, ToAVLTreeNode **root);
void left_turn(ToAVLTreeNode *p, ToAVLTreeNode *c, ToAVLTreeNode **root);
void right_left_turn(ToAVLTreeNode *p, ToAVLTreeNode *c, ToAVLTreeNode **root);
void left_right_turn(ToAVLTreeNode *p, ToAVLTreeNode *c, ToAVLTreeNode **root);

void add_node(int value, ToAVLTreeNode **root){
    ToAVLTreeNode *new_node = (ToAVLTreeNode *)malloc(sizeof(ToAVLTreeNode));
    ToAVLTreeNode *node = *root, *previous_node = NULL;
    int child_mark = 0;
    
    while (node != NULL){
        previous_node = node;
        if (value < node->value){
            node = node->lchild;
            child_mark = 1;
        }
        else if(value > node->value){
            node = node->rchild;
            child_mark = 2;
        }
        else{
            node->count += 1;
            child_mark = -1;
            break;
        }
    }
    
    switch (child_mark){
        case 1:previous_node->lchild = new_node;break;
        case 2:previous_node->rchild = new_node;break;
        case 0:*root = new_node;break;
    }
    
    if (child_mark != -1){
        new_node->value = value;
        new_node->count = 1;
        new_node->balance_factory = 0;
        new_node->child_mark = child_mark;
        new_node->lchild = NULL;
        new_node->rchild = NULL;
        new_node->father = previous_node;
    }else{
        free(new_node);
        new_node = NULL;
    }
    
    flush_balance_factory(new_node, root);
}

void flush_balance_factory(ToAVLTreeNode *node, ToAVLTreeNode **root){
    // mark和mark_node 是在更新完一次平衡因素后，用于判断是使用左旋，右旋，左右旋，右左旋
    int mark[2] = {0, 0};
    ToAVLTreeNode *mark_node[2] = {NULL, NULL};
    
     // 旋转可能导致根节点发生改变,所以我们将指想根节点的指针的地址传递给旋转函数，用于修改根节点
    while (node != NULL && node->father != NULL){
        if (node->child_mark == 1){
            node->father->balance_factory -= 1;
        }
        else if (node->child_mark == 2){
            node->father->balance_factory += 1;
        }
        mark[1] = mark[2];
        mark[2] = node->child_mark;
        mark_node[1] = mark_node[2];
        mark_node[2] = node->father;
        
        node = node->father;
        if (node->balance_factory == 0){
            break;
        }
        else if (node->balance_factory == 2){
            // 调用左旋函数或者右旋左旋函数
            if (mark[1] == 1){
                right_left_turn(mark_node[2], mark_node[1], root);
            }
            else if (mark[1] == 2){
                left_turn(mark_node[2], mark_node[1], root);
            }
            break;
        }
        else if (node->balance_factory == -2){
            //调用右旋函数或者左旋右旋函数
            if (mark[1] == 1){
                right_turn(mark_node[2], mark_node[1], root);
            }
            else if (mark[1] == 2){
                left_right_turn(mark_node[2], mark_node[1], root);
            }
            break;
        }
    }
}

void front_traverse(ToAVLTreeNode *head){
    if (head != NULL){
        printf("%d,", head->value);
        front_traverse(head->lchild);
        front_traverse(head->rchild);
    }
}

void right_turn(ToAVLTreeNode *p, ToAVLTreeNode *c, ToAVLTreeNode **root){
    ToAVLTreeNode *s2 = c->rchild;
    p->lchild = s2;
    if (s2 != NULL){
        s2->father = p;
    }
    
    c->father = p->father;
    c->child_mark = p->child_mark;
    if (p->father != NULL){
        if (p->child_mark == 1){
            p->father->lchild = c;
        }
        else if (p->child_mark == 2){
            p->father->rchild = c;
        }
    }
    else{
        *root = c;
    }
    
    c->balance_factory = 0;    
    c->rchild = p;
    p->child_mark = 2;
    p->balance_factory = 0;
    p->father = c;
}

void left_turn(ToAVLTreeNode *p, ToAVLTreeNode *c, ToAVLTreeNode **root){
    ToAVLTreeNode *s2 = c->lchild;
    p->rchild = s2;
    if (s2 != NULL){
        s2->father = p;
    }
    
    c->father = p->father;
    c->child_mark = p->child_mark;
    if (p->father != NULL){
        if (p->child_mark == 1){
            p->father->lchild = c;
        }
        else if (p->child_mark == 2){
            p->father->rchild = c;
        }
    }
        else{
        *root = c;
    }
    
    c->balance_factory = 0;
    c->lchild = p;
    p->child_mark = 1;
    p->balance_factory = 0;
    p->father = c;

}

void right_left_turn(ToAVLTreeNode *p, ToAVLTreeNode *c, ToAVLTreeNode **root){
    ToAVLTreeNode *g = c->lchild;
    ToAVLTreeNode *s2 = g->lchild;
    p->rchild = s2;
    if (s2 != NULL){
        s2->father = p;
    }
    
    ToAVLTreeNode *s3 = g->rchild;
    c->lchild = s3;
    if (s3 != NULL){
        s3->father = c;
    }
    
    g->father = p->father;
    g->child_mark = p->child_mark;
    if (p->father != NULL){
        if (p->child_mark == 1){
            p->father->lchild = g;
        }
        else if (p->child_mark == 2){
            p->father->rchild = g;
        }
    }
    else{
        *root = g;
    }
    
    g->lchild = p;
    p->father = g;
    p->child_mark = 1;
    g->rchild = c;
    c->father = g;
    c->child_mark = 2;
    
    if (g->balance_factory == -1){
        p->balance_factory = 0;
        c->balance_factory = 1;
    }
    else{
        p->balance_factory = -1;
        c->balance_factory = 0;
    }
    
    g->balance_factory = 0;
}

void left_right_turn(ToAVLTreeNode *p, ToAVLTreeNode *c, ToAVLTreeNode **root){
    ToAVLTreeNode *g = c->rchild;
    ToAVLTreeNode *s3 = g->rchild;
    p->lchild = s3;
    if (s3 != NULL){
        s3->father = p;
    }
    
    ToAVLTreeNode *s2 = g->lchild;
    c->rchild = s2;
    if (s2 != NULL){
        s2->father = c;
    }
    
    g->father = p->father;
    g->child_mark = p->child_mark;
    if (p->father != NULL){
        if (p->child_mark == 1){
            p->father->lchild = g;
        }
        else if (p->child_mark == 2){
            p->father->rchild = g;
        }
    }
    else{
        *root = g;
    }
    
    g->lchild = c;
    c->father = g;
    c->child_mark = 1;
    g->rchild = p;
    p->father = g;
    p->child_mark = 2;
    
    if (g->balance_factory== -1){
        c->balance_factory = 0;
        p->balance_factory = 1;
    }
    else if (g->balance_factory == 1){
        c->balance_factory = -1;
        p->balance_factory = 0;
    }
    g->balance_factory = 0;
}

int main(void){

***待补充***