基础算法（二）（待完善）

内容概要

　　一、快速排列、代码实现、复杂度计算

　　二、堆排序前置知识：树相关、二叉树、堆

　　三、堆排序算法、代码实现、复杂度计算

　　四、归并排序算法、代码实现、复杂度计算

 

1、快速排列、代码实现、复杂度计算

 　　**这里的快速排序和我之前写的思路不太一样（这个更好理解，代码也更简单），但核心思想没有变**

　　快速排序的核心思想

　　　　取列表中一个数，进行一次排序，使得这个数左边所有数都小于这个数、这个数右边所有数都大于这个数。

　　　　递归调用归位函数，实现排序

 

　　快速排序图解

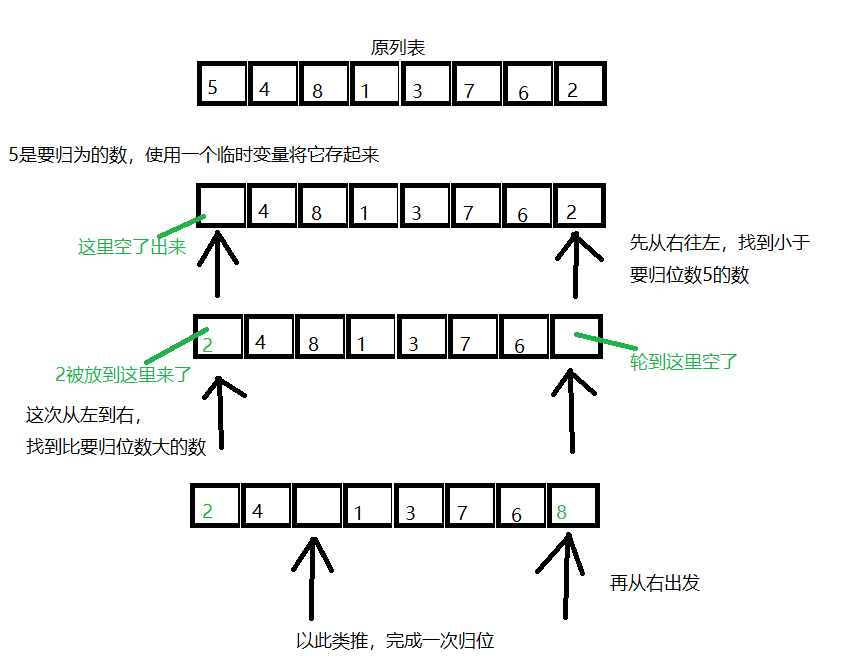
　　一次归位函数实现

def position(li, head, end):
    tmp = li[head]
    while head < end:
        while head < end and li[end] >= tmp:
            end -= 1
        li[head] = li[end]
        while head < end and li[head] <= tmp:
            head += 1
        li[end] = li[head]
    li[head] = tmp
    return head

　　递归调用一次归位函数实现快速排列

def quick_sort(li, head, end):
    if head < end:         mid = position(li, head, end)
        quick_sort(li, head, mid-1)
        quick_sort(li, mid+1, end)

 

2、树相关、二叉树、堆

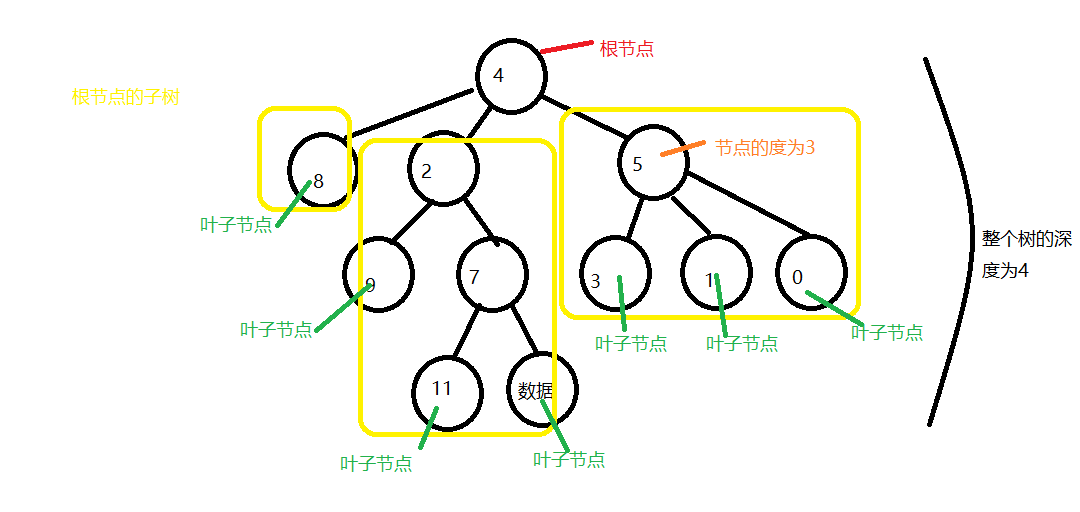
　　树是一种数据结构

　　　　树的相关概念

　　　　　　-根节点

　　　　　　　　所有节点最终汇聚到的节点

　　　　　　-子树

　　　　　　-树（子树）的深度

　　　　　　-树（子数）的度

　　　　　　　　树（子树）的度可以理解为树的根节点（子树的根节点）的分支数

　　　　　　-孩子节点，父节点

　　　　　　　　父节点和孩子节点的关系是相对的

　　　　　　-叶子节点

　　　　　　　　没有孩子节点的就是叶子节点

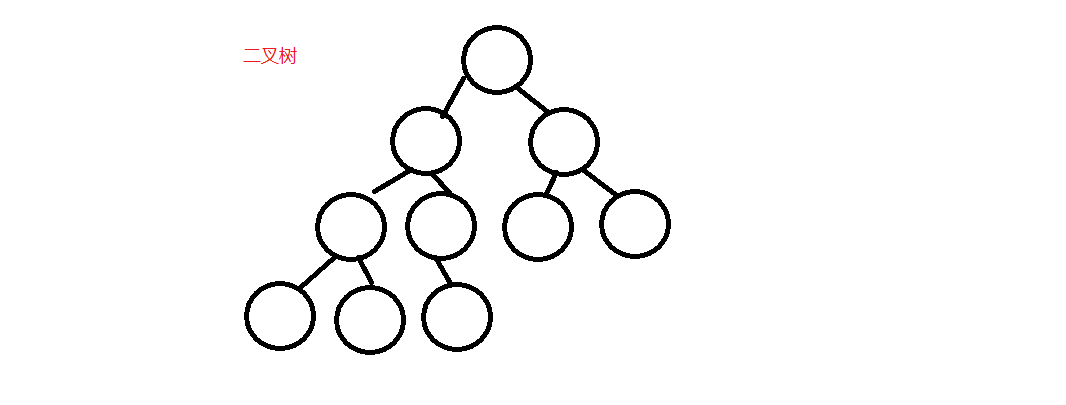
　　二叉树是一种特殊的树，它的每个节点的度都小于等于2

　　满二叉树

　　　　叶子节点均在同一级，其余所有节点的度都为2的二叉树

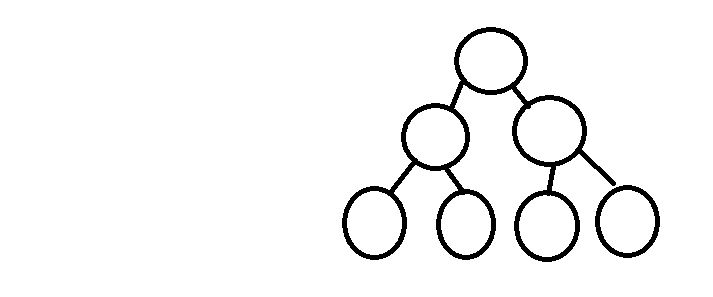
　　完全二叉树

　　　　叶子节点只能出现在最下层和次下层，次下层的节点都必须存在，并且最下层叶子节点是从左往右不间断出现的

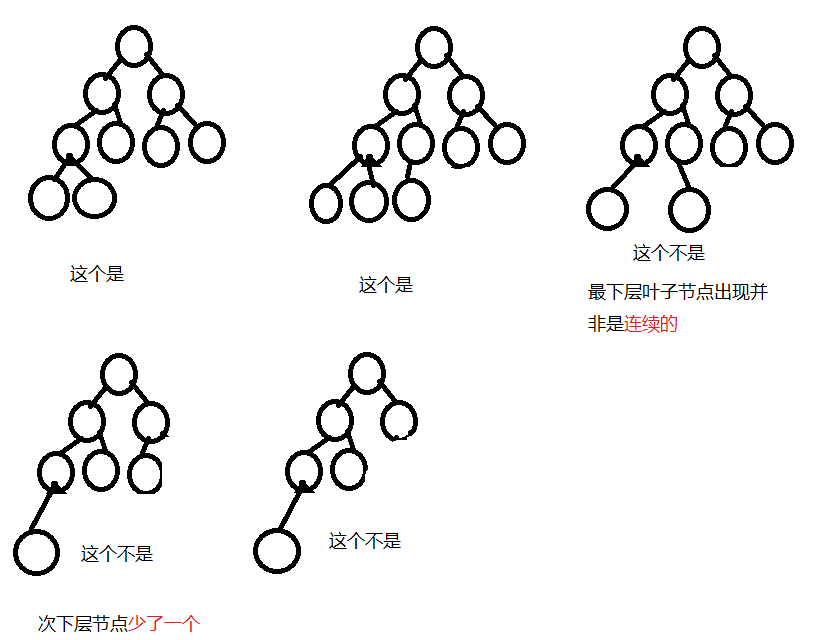
　　　　完全二叉树的定义缘由可能与完全二叉树数据结构的实现方式有关

 

　　数据结构中的堆指的是特殊的完全二叉树

　　　　堆具体分为大根堆和小根堆

　　　　　　大根堆：

　　　　　　　　父节点比两个孩子节点都大的完全二叉树

　　　　　　小根堆：
　　　　　　　　父节点比两个孩子节点都小的完全二叉树

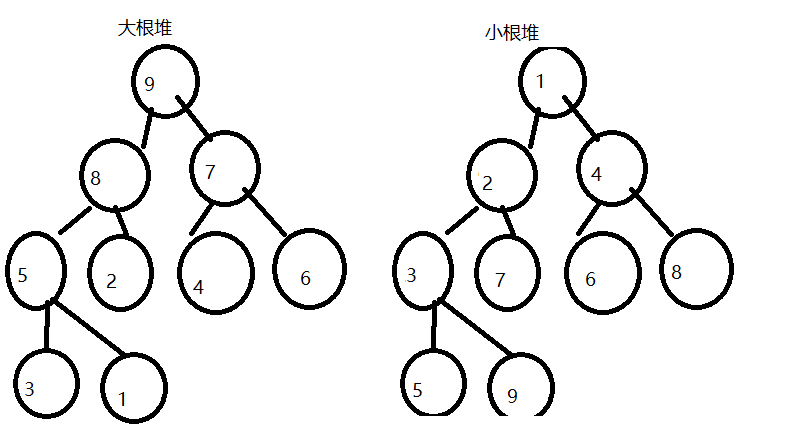
　　　　大根堆、小根堆特点：

　　　　　　大根堆根节点一定是所有节点中最大的数，小根堆则相反

 

　　堆数据结构的两种组织方式

　　　　一、链式存储方式

　　　　　　　　***待补充***

 

　　　　二、顺序存储方式

　　　　　　　　以列表为例

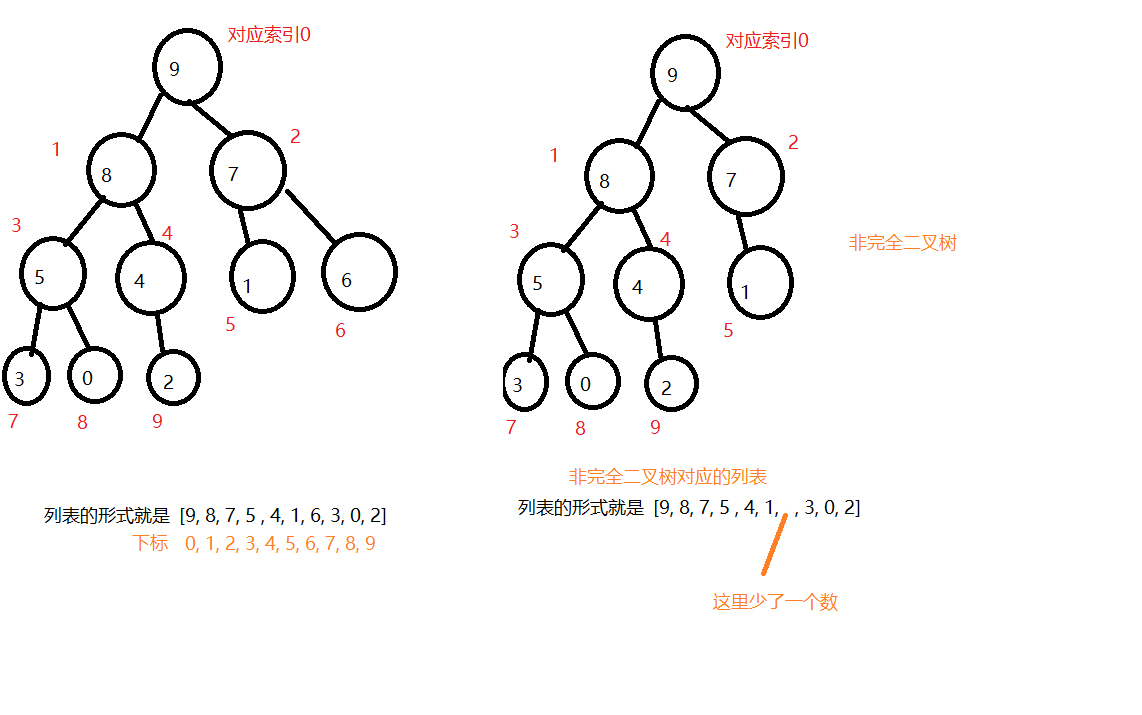
　　　　顺序方式下，父节点索引与孩子节点索引的关系

　　　　　　父节点的索引为  i

　　　　　　　　-左孩子的索引为  i * 2 + 1

　　　　　　　　-右孩子的索引为  i * 2 + 2

 

3、堆排序的代码实现，时间复杂度计算

　　堆排序三大步骤

　　　　-1、完成向下调整函数

　　　　-2、构建堆

　　　　-3、挨个出数

 

　　堆向下调整原理

 　　　　对于一个完全二叉树，如果根节点的两个子树都是大根堆或者小根堆，那么可以通过堆的向下调整原理，将整个完全二叉树变为堆

 

 

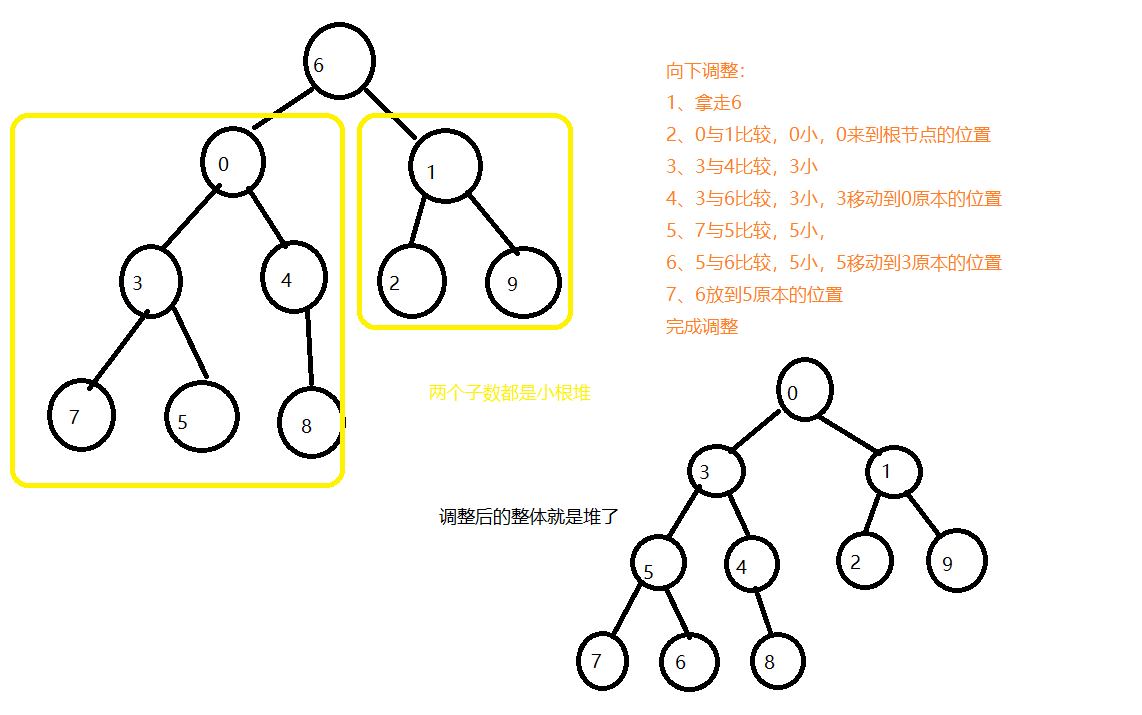
　　-堆向下调整代码实现

　　　　使用的是python，用c语言会有点复杂

# 对于一个已经是堆的列表
li = [9, 7, 8, 5, 4, 6, 1, 2, 3]

father_index = 0
move_index = 0
end_index = len(li) - 1

while end_index > 0:
    li[0], li[end_index] = li[end_index], li[0]
    end_index -= 1  # 堆最后一个元素
    move_index = 0  # 要移动的元素的下标

    while move_index * 2 + 1 <= end_index:
        has_right_index = True
        has_exchange = False
        father_index = move_index  # move_index是移动的元素的下标，它是可变的
        right_index = father_index * 2 + 2
        left_index = father_index * 2 + 1

        if right_index > end_index:  # 判断是否有右孩子节点
            has_right_index = False

        if li[father_index] < li[left_index]:
            li[father_index], li[left_index] = li[left_index], li[father_index]
            move_index = move_index * 2 + 1
            has_exchange = True

        if has_right_index and li[father_index] < li[right_index]:
            li[father_index], li[right_index] = li[right_index], li[father_index]
            if move_index == father_index:  # 如果移动的元素已经移动到左孩子节点，那么就不需要改变move_index的值了
                move_index = move_index * 2 + 1
                has_exchange = True

        if not has_exchange:  # 如果没有移动说明已经是最大值了
            break

print(li)

　　　　视频中的代码

def sift(li, head, end):
    """
    :param li: 列表
    :param head: 堆的根节点位置
    :param end: 堆的最后一个元素的位置
    :return:
    """
    i = head  # i最开始指向根节点
    j = i * 2 + 1  # j开始是左孩子
    tmp = li[head]  # 将要调整的值存放
    while j <= end:  # 验证i是否是叶子节点，j是否越界列表
        if j + 1 <= end and li[j] < li[j + 1]:  # 如果右孩子有并且比较大
            j += 1  # j指向右孩子
        if tmp < li[j]:  # 如果目标比孩子小，将大的孩子移动到父节点位置
            li[i] = li[j]
            i = j  # 往下探一层
            j = i * 2 + 1
        else:  # tmp更大，就
            # li[i] = tmp
            break
    #else:
    li[i] = tmp

 

　　　　构建堆函数实现

　　　　　　这个是错误的

 

def create(li):
    first = True
    end = len(li) - 1

    while (end - 2) // 2 >= 0:
        if first and end % 2 == 1:  # 条件满足证明开时为左孩子
            head = (end - 1) // 2  # 获取父节点索引
            if li[head] < li[end]:  # 如果父节点值小于左孩子节点的值
                li[head], li[end] = li[end], li[head]
            end -= 1  # 指向下一个堆的右孩子节点
            first = False

        head = (end - 2) // 2

        max_val = end  # 默认将右节点的索引设为大值

        if li[end] < li[end - 1]:  # 如果右孩子的值小于左孩子，将max_val指向左孩子
            max_val = end - 1

        if li[head] < li[max_val]:
            li[head], li[max_val] = li[max_val], li[head]

        end -= 2

 

　　　　　　写错了好多次写出来了（可读性一点没有）

def create(li):
    end = len(li) - 1
    relate_li = []

    tmp_head = end
    while tmp_head > 0:
        if tmp_head % 2 == 1:
            tmp_head = (tmp_head - 1) // 2
        else:
            tmp_head = (tmp_head - 2) // 2
        relate_li.append(tmp_head)

    if end % 2 == 1:
        head = (end - 1) // 2
    else:
        head = (end - 2) // 2

    # 将子树变成堆
    while head >= 0:
        # 找到子树的结束索引
        right_index = head * 2 + 2
        while right_index <= end:
            if head in relate_li:
                tmp_end = end
                break
            else:
                right_index = right_index * 2 + 2
        else:
            tmp_end = (right_index - 2) // 2

        sift(li, head, tmp_end)
        head -= 1

 

　　　　　　自己的改良版本（吐了）

def create2(li, end):
    head = (end - 1) // 2  # 第一个发现：对于堆的最后一个节点，无论它是左孩子节点还是右孩子节点，它的父节点都可以通过这个式子求出
    while head >= 0:
        sift(li, head, end)  # 第二个发现：对于整个二叉树内的任意一个子树，都可以统一使用end作为判断是否到达叶子节点的条件，而不需要动态获取当前子树的最后一个节点的索引
        head -= 1

　　　　　　牛逼的清华大佬的牛逼代码（构建堆循环加挨个出数循环）

def heap_sort(li):
    n = len(li) - 1
    for i in range((n-1)//2, -1, -1):  # 构建堆
        sift(li, i, n)
    
    for i in range(n, 0, -1):  # 挨个出数
        li[0], li[i] = li[i], li[0]
        sift(li, 0, i-1)

 

　　　　挨个出数函数实现

def heap_out(heap):
    end = len(heap) - 1
    while end > 0:
        heap[0], heap[end] = heap[end], heap[0]
        end -= 1
        sift(heap, 0, end)

 

　　堆排序的复杂度计算

def sift(li, head, end):
    """
    :param li: 列表
    :param head: 堆的根节点位置
    :param end: 堆的最后一个元素的位置
    :return:
    """
    i = head
    j = i * 2 + 1
    tmp = li[head]
    while j <= end: 
        if j + 1 <= end and li[j] < li[j + 1]:
            j += 1
        if tmp < li[j]:
            li[i] = li[j]
            i = j
            j = i * 2 + 1
        else:
            break
    li[i] = tmp


def heap_sort(li):
    n = len(li) - 1
    for i in range((n - 1) // 2, -1, -1):  # 构建堆
        sift(li, i, n)

    for i in range(n, 0, -1):  # 挨个出数
        li[0], li[i] = li[i], li[0]
        sift(li, 0, i - 1)

　　　　对于向下调整函数，因为有折半的过程，它的复杂度可以看作是O(logn)

　　　　对于构建堆循环和挨个出数循环，它们的复杂度是O(n)（构建堆循环复杂度为O(1/2n),常数1/2省略；挨个出数循环复杂度为O(n),两者合一的复杂度视为O(n)）

　　　　所以整个堆排序的复杂度为O(nlogn)

 

4、归并排序算法、代码实现、复杂度计算

　　归并排序的思想

　　　　将两个有序的数据合并为一个新的有序数据

　　　　通过递归从最少的元素开始构造有序数据，有序数据长度逐渐增大，最后完成排序

 

　　一次归并函数原理、代码实现

　　　　假设有一个列表，它可以看作是两个有序列表的结合

　　　　-一次归并函数图解

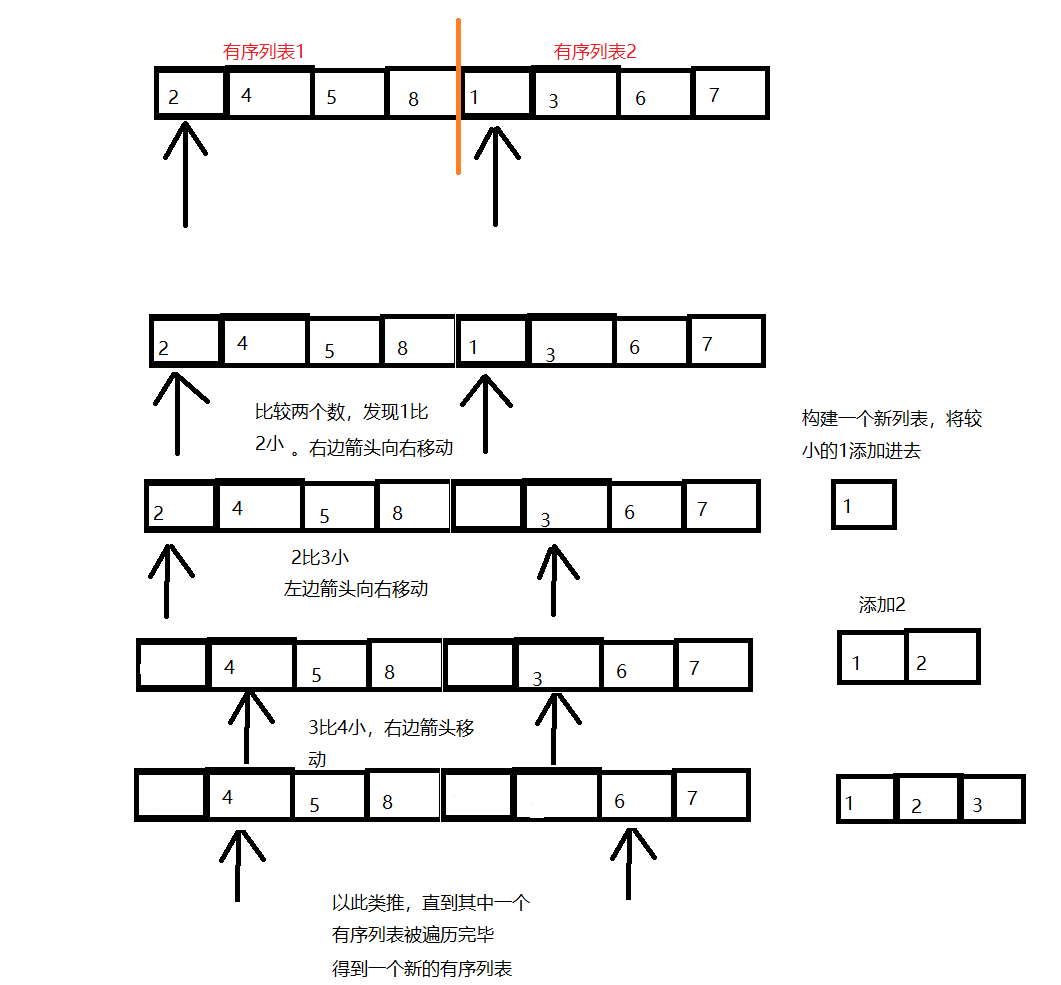
　　　　-代码实现

 

def merge(li, head, mid, end):
    i = head  # i用于遍历第一个有序列表
    j = mid+1  # j用于遍历第二个有序列表
    tmp_li = []  # 存放重新排序的数
    while i <= mid and j <= end:  # 当其中一个有序列表被遍历完毕，无法再比较两个列表的值的大小
        if li[i] <= li[j]:  # 左列表的数比右列表小或者等于时，将这个值添加到新列表中
            tmp_li.append(li[i])
            i += 1
        else:  # 右列表的数比左列表要小
            tmp_li.append(li[j])
            j += 1
    
    while i <= mid:  # 将另外一个有序列表中剩余的数都添加到新列表中
        tmp_li.append(li[i])
        i += 1
    while j <= end:
        tmp_li.append(li[j])
        j += 1

    li[head:end+1] = tmp_li  # 使用临时列表替换原列表，列表切片的特殊用法

 

　　递归调用一次归并函数实现排序

　　　　对于一个完全随机的列表——[2, 5, 3, 4, 8, 1,7, 6]

　　　　递归图解

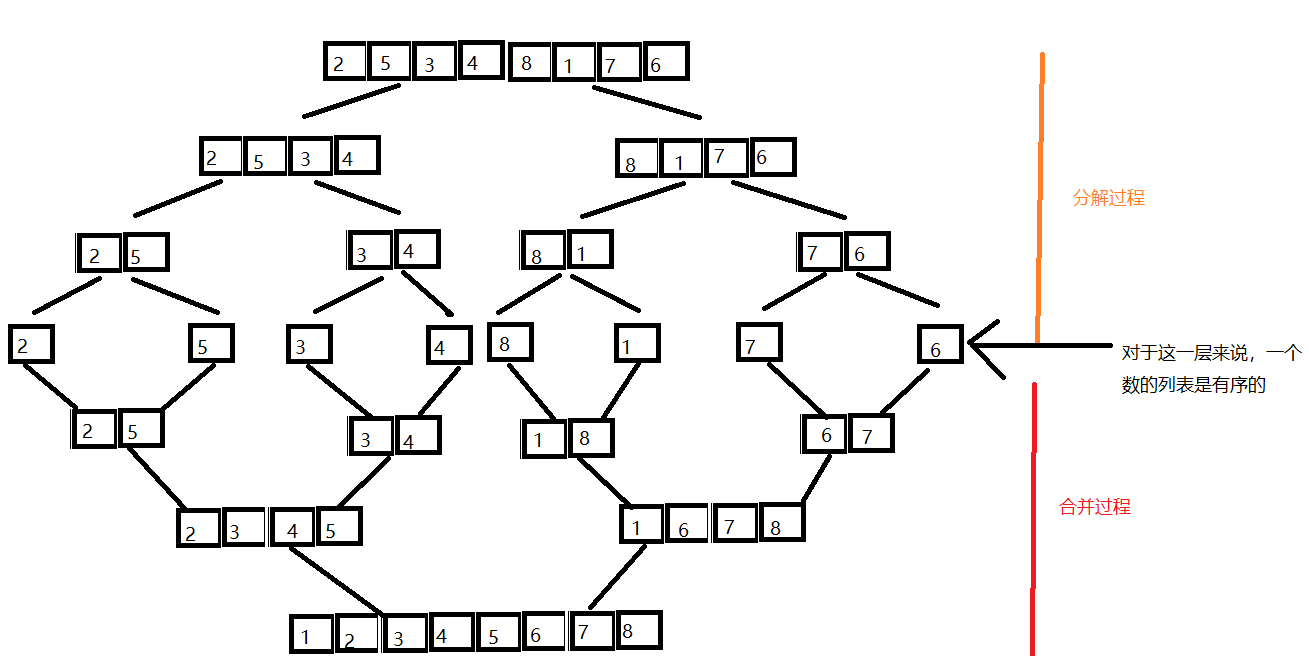
　　　　归并代码实现

def merge_sort(li, head, end):
    if head < end:  # 当这个列表至少有两个数时，才进行排序；为1个和0个时，没有排序必要
        mid = (head + end) // 2
        merge_sort(li, head, mid)  # 先递归把左边排好
        merge_sort(li, mid+1, end)  # 再递归把右边排好
        merge(li, head, mid, end)  # 左右边都排好就可以进行一次归并了

 

　　归并排序复杂度计算

　　　　-归并排序要使用到递归，由于每次递归减半，递归次数为logn次，可以将递归过程的复杂度看作为O(logn)

　　　　-由上图，每一层递归都要遍历列表的所有数据，所以每一层递归的复杂度可以看作O(n)

　　　　综上，归并排序的复杂度是O(nlogn)

 

***待完善***