计算机运算-二进制编码

整数的二进制计算

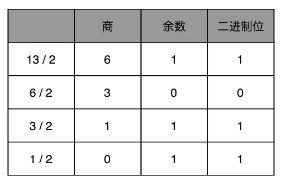
整数的二进制计算比较简单，其实就是每位逢二进一，而10进制转换二进制用短除法即可，不断除以二，每次的余数连起来就是二进制表示的值。
原码表示法：简单粗暴的用最左位表示符号正负，负1正0，例如：1011就是-3，0011就是3，这种表示法会导致0000和1000都是0，浪费了一位。
补码表示法：补码表示法比较特殊，例如：一个 4 位的二进制补码数值 1011，转换成十进制，就是 −1×2³+0×2²+1×2¹+1×2⁰，也就是最高位为负数，其他为正数相加的和；这种方式有两个好处：1.只有0000是0,1000是最小的负数，少占用一位。2.这种表示方式完全符合二进制的加减法，不需要特殊处理。
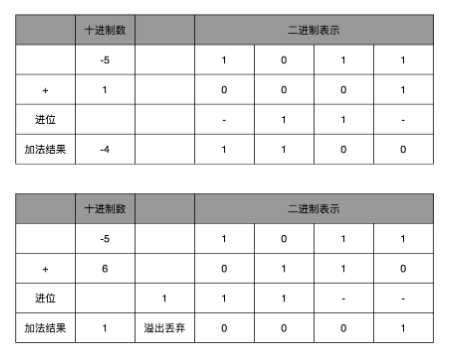
如下两个加法：

有几个特殊的情况需要说明下：
1.0000表示0，减一之后会变成1111表示-1，持续-1会变成最小的数1000也就是-8。
2.java中左移右移分成有符号和无符号，如下所示，解释了为什么无符号右移会导致负数突然变成最大的正数。另外，没有无符号左移，因为左移本身就是无符号的。另外，溢出的场景这里不考虑，因为很特殊。

        System.out.println(-1>>1);//-1 也就是1111..1=>1111....1，有符号右移会自动补位1
        System.out.println(-1>>3);//-1 也就是1111..1=>1111....1，有符号右移会自动补位1
        System.out.println(-1>>>1);//2147483647 也就是1111..1=>0111....1，无符号右移只会补0
        System.out.println(-1<<1);//-2 也就是1111..1 => 1111..0，左移也只会补0
        System.out.println(-1<<31);//-2147483648 也就是1111..1 => 1000..0，左移也只会补0
        System.out.println(1>>1);//0 也就是 0000..1 => 0000..0，右移也只会补0
        System.out.println(1>>>1);//0 也就是 0000..1 => 0000..0，是否有符号对正数没什么区别，因为高位都是0
        System.out.println(1<<1);//2 也就是 0000..1 => 0000..10
        System.out.println(Integer.MAX_VALUE<<1);//-2 也就是 0111..1 => 1111..10，左移本身就是无符号的

3.例如integer 32位，可以表示的值是从-2³¹ 到 2³¹-1，因为正数里占用了个0，所以会少一种表示正数的位，同时最高位用作了符号位，所以可能性只有1次方。

字符串的二进制表示

下面这个图片就是ASCII码（American Standard Code for Information Interchange，美国信息交换标准代码）

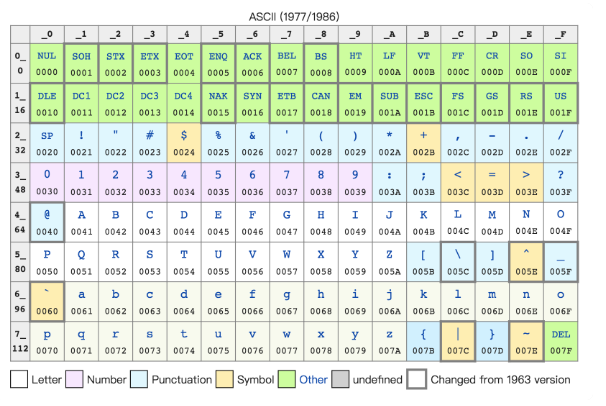
其实就是用不同的二进制数映射不同的字符串内容，包括英文字母、数字、标点符号等。这种表示方式非常灵活，只要编写不同的交换标准代码，就可以映射中文、韩文、日文等文字。
但是日常使用中，需要注意字符串保存占用的空间是很大的，例如最大的32位整数，就是2147483647。如果用整数表示法，只需要 32 位就能表示了。但是如果用字符串来表示，一共有 10 个字符，每个字符用 8 位的话，需要整整 80 位。比起整数表示法，要多占很多空间。如果用中文，码的位数更多，也会需要更多存储空间。不管是整数也好，浮点数也好，采用二进制序列化会比存储文本省下不少空间。

日常编码出现的乱码就是字符集（Charset）和字符编码（Character Encoding）不同导致的。

浮点数的二进制表示

之前讲了整数、字符串、还有个关键的小数没讲到。在计算机中我们常用的float和double是无法表示精确地非二分数的，它只能表示(1/2)¹，(1/2)²，(1/2)²，也就是0.5，0.25，0.125这种数字，但是没法准确表示0.3，0.9，这是由于它特殊的编码方式决定的。

BCD编码

BCD编码（Binary-Coded Decimal）比浮点数好在可以准确表示十进制的各种小数位，十进制的个位是0-9，它就用4bit来表示0-9的各个数字。

表示方式如下：
用16bit表示了1024这个数字，这种编码方式在超市、银行很好用。

0001	0000	0010	0100
1	0	2	4

很明显，这个表达方式有几个明显的问题：
1.16bit原本可以表示2¹⁶个数字，约等于6.5W个数字，而10⁴个数字只有1W个数字，缩水了6倍左右。
2.这样的表示方式没办法同时表示很大的数字和很小的数字，如果我们需要表示光速：3×10⁸，那这个数字就要到32位了，或者要表示0.0000000001，那就又得扩位了。

浮点数

为了解决BCD编码的问题，可以用浮点数（IEEE标准）来表示，浮点数的FLOAT表现形式是：一个公式+32Bit的占位符。
公式：(−1)^s×1.f×2^e
32Bit占位符：

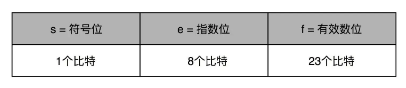
我们可以以 0.5 为例子。0.5 的符号为 s 应该是 0，f 应该是 0，而 e 应该是 -1，也就是0.5=(−1)0×1.0×2−1=0.5，对应的浮点数表示，就是 32 个比特。

第一部分是一个符号位，用来表示是正数还是负数。我们一般用 s 来表示。
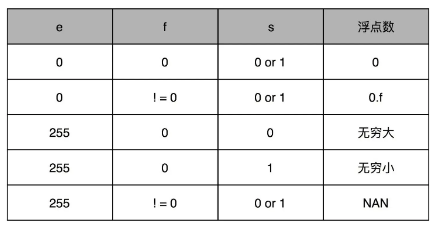
接下来是一个 8 个比特组成的指数位。我们一般用 e 来表示。8 个比特能够表示的整数空间，就是 0～255。我们在这里用 1～254 映射到 -126～127 这 254 个有正有负的数上。因为我们的浮点数，不仅仅想要表示很大的数，还希望能够表示很小的数，所以指数位也会有负数。你发现没，我们没有用到 0 和 255。没错，这里的 0（也就是 8 个比特全部为 0）和 255 （也就是 8 个比特全部为 1）另有它用，如下图所示，它表示了一些其他的数值。
最后，是一个 23 个比特组成的有效数位。我们用 f 来表示。

浮点数可以表示：3.40×10³⁸到 1.17×10^-38的数字范围。

浮点数的二进制转换

假如我们有一个浮点数9.1，我们想把他表示为二进制：
1.整数9部分，使用二除法，表示很简单就是1001。
2.小数部分和整数相反，使用二乘法，如下图，

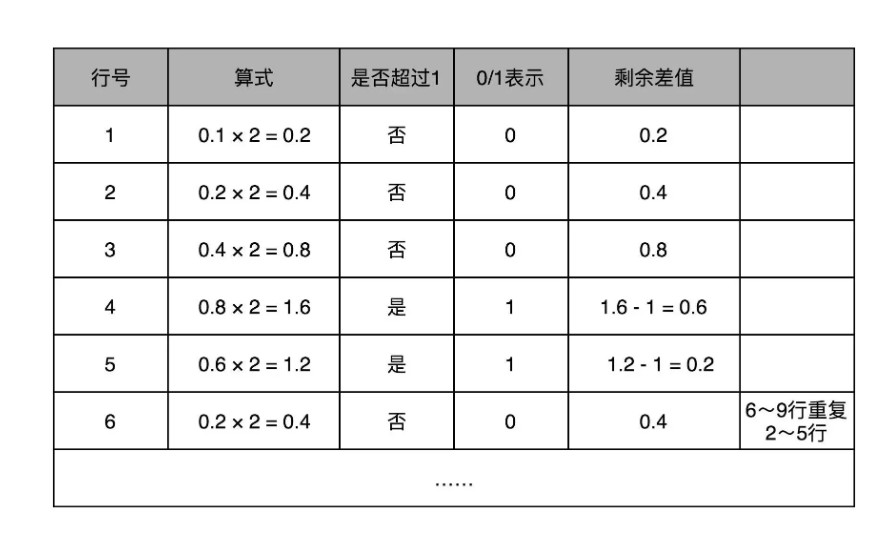
然后，9.1 这个十进制数就变成了 1001.0001100110011.....，省略位数并控制循环位，最终形成的Float浮点数1.001000110011…×23

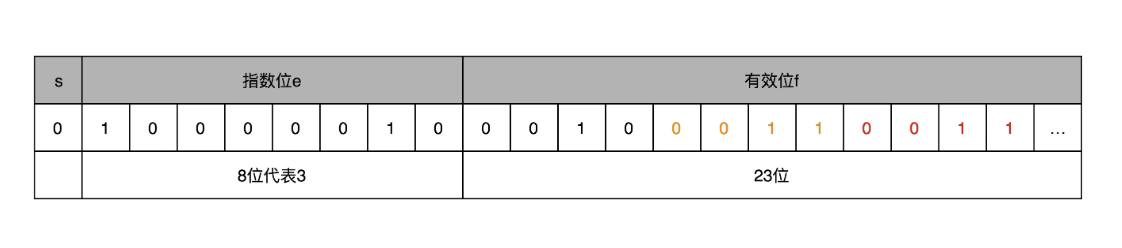
如果我们把它再转换成10进制，就约等于9.09999942779541015625，差不多就相当于9.1，这个值就是浮点数的不精准的问题由来。

作者给了个链接，可以直观展示浮点数位：浮点数实时展示

浮点数的加法和精度损失

浮点数的加法和指数加法一样，要先对齐，再相加，我们举个例就知道浮点数如何相加了：0.125+0.5。

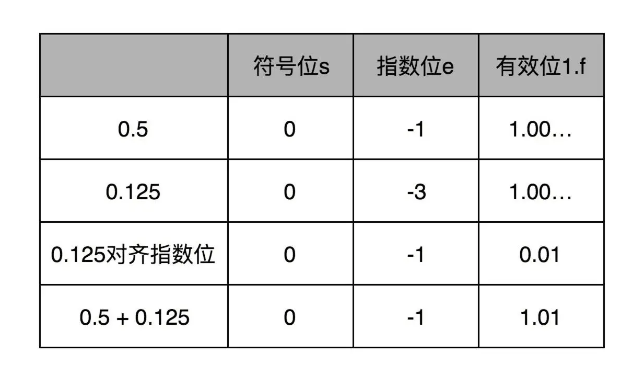
如上图:
0.125=(-1)⁰×1.0×2^-3
0.5 =(-1)⁰×1.0×2^-1
将两者指数位对齐后：
0.125=(-1)⁰×0.01×2^-1
0.5 =(-1)⁰×1.0×2^-1
相加=(-1)⁰×1.01×2^-1，结果就是0.625，浮点数的加法就这么简单。

但我们发现了一个问题，指数位比较小的数需要被迫右移，如果是0.1这种无限循环小数，其小数位右移后有效位会丢弃（f一共只有23位），所以浮点数如果两个数大小差距很大，会导致精度丢失。

Kahan Summation 算法

一次精度丢失似乎没问题，但如果是个累加算法，连续累加2000万个1，但是结果到1600万之后就停止了，因为1600万之后加的1都因为精度损失没了，这是不能接受的。

如下是python代码表示的Kahan Summation 算法

def kahan_summation(numbers):
    summation = 0.0
    c = 0.0

    for number in numbers:
        y = number - c
        t = summation + y
        c = (t - summation) - y
        summation = t

    return summation

mysql的decimal和java的bigdecimal是怎么保证精度的

ChatGPT的回答很棒，稍微改改就能直接用

MySQL 中的 DECIMAL 类型和 Java 中的 BigDecimal 类都是为了解决浮点数计算中精度损失问题而设计的。它们通过存储和计算数值的精确表示来实现精确的计算，而不是依赖二进制浮点数的近似表示。

MySQL 中的 DECIMAL 类型：
MySQL 中的 DECIMAL 类型是一种定点数数据类型，可以存储精确的小数值。与浮点数类型不同，DECIMAL 类型将数字作为字符串来存储，其中每个字符代表一个十进制数字。在计算过程中，MySQL 会使用定点数算法而不是浮点数算法，以保证数值计算的精确性。（定点数数据类型是指对整数和小数位确定位数的数据类型，所以可以分开存储，把小数位也当整数位一样计算，就不会有精度丢失的问题）

DECIMAL 类型允许您指定精度（总的有效数字）和小数点后的位数（小数部分的有效数字）。例如，DECIMAL(10,2) 表示最多可以存储 10 位有效数字，其中小数点后有 2 位。

Java 中的 BigDecimal 类：
Java 中的 BigDecimal 类也是为了解决浮点数精度损失问题而设计的。BigDecimal 类表示任意精度的有符号十进制数。它将数值存储为一个整数 unscaledValue 和一个整数 scale，其中 unscaledValue 表示未缩放的值，scale 表示小数点右移的位数。例如，数值 123.45 可以表示为 unscaledValue = 12345 和 scale = 2。
BigDecimal的内部实现使用BigInteger类来存储unscaledValue，BigInteger类可以表示任意大小的整数。

总之，MySQL 中的 DECIMAL 类型和 Java 中的 BigDecimal 类的思想一样：都是通过把小数转换为整数进行计算，二进制计算整数还是正确的，然后再转换小数点的位数，保证了精度准确。

posted @ 2023-03-28 10:02 来焕明阅读(1321) 评论(0) 收藏举报

刷新页面返回顶部