结对编程作业
一、项目及分工
博客地址
队友的博客地址:https://www.cnblogs.com/llhhlh/
我的博客地址:https://www.cnblogs.com/l523/
项目地址
分工
| 原型设计 | 游戏 | AI | 解题及改良 | |
|---|---|---|---|---|
| 李赫 | √ | √ | √ | |
| 李志炜 | √ | √ | √ |
二、原型设计
设计说明
- 这次结对编程,我们先看了看市面上已开发好的数字华容道和拼图游戏,学习了一下别人的优秀项目,听柯老板的--站在巨人的肩膀上。
看了这样的项目:
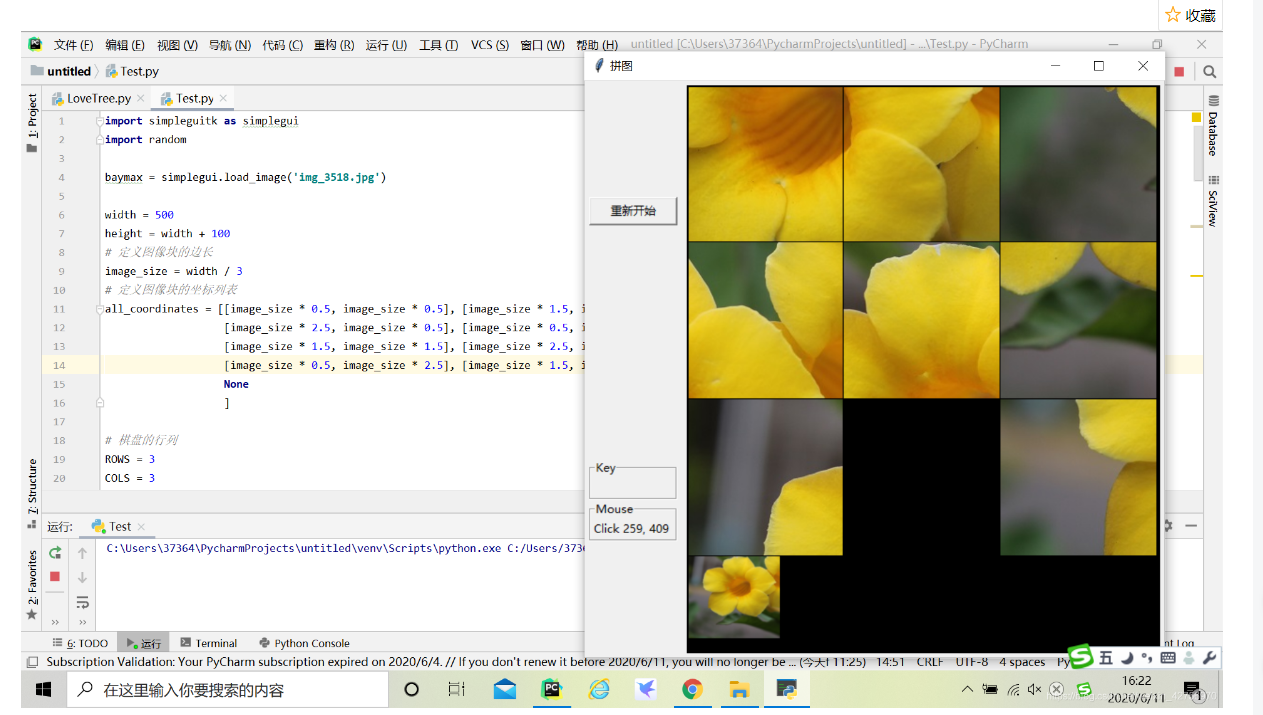
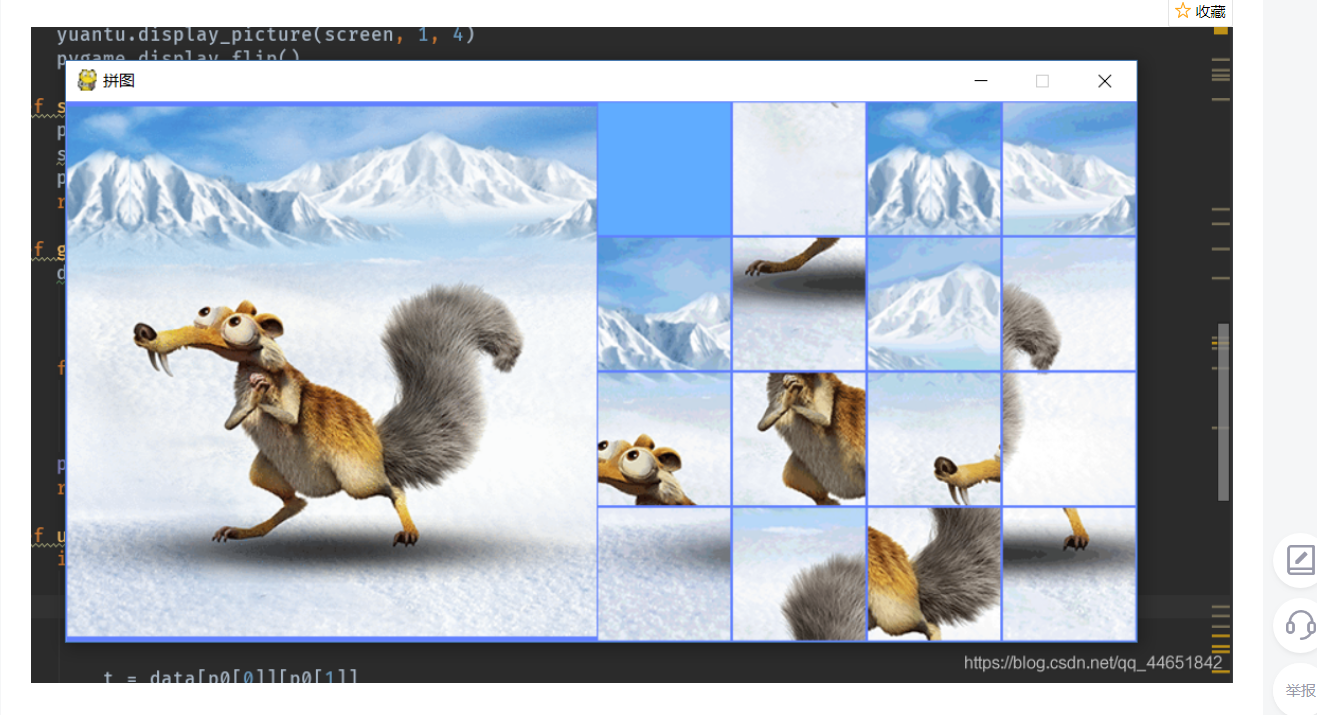
还看了这样的:
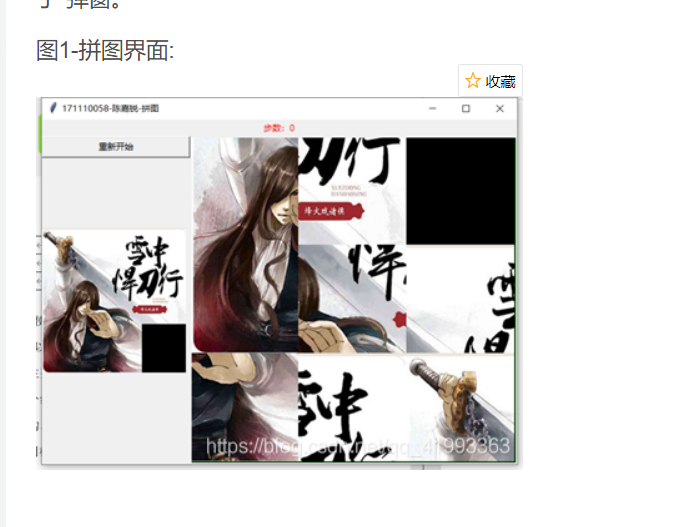
最后设想的我们的原型要至少能够实现能玩的功能,在能够玩的基础上,尝试增加在一定步数让其中两张图片强制交换,还有内嵌AI在玩家不知如何走时提示下一步可以的走法和实现自动帮助玩家复原。
原型
我们的原型是这样的:
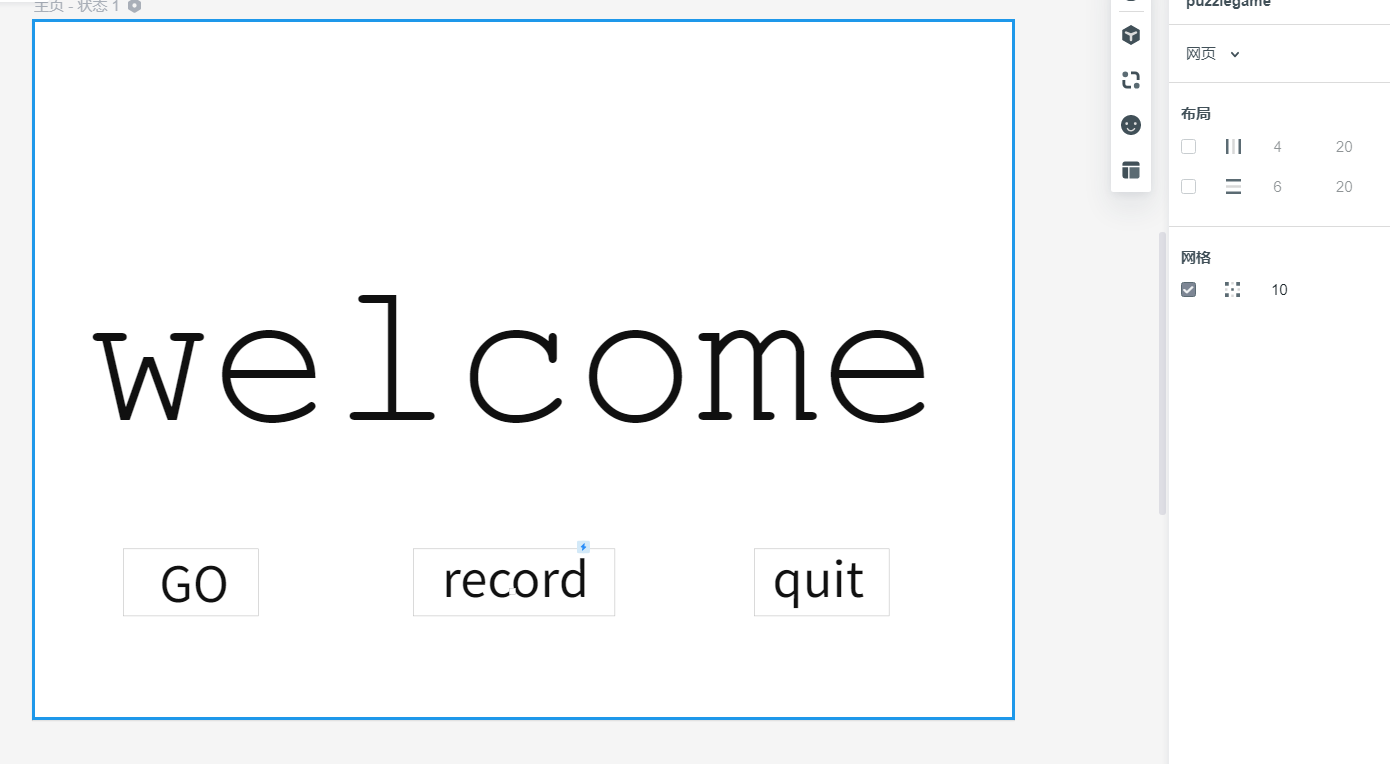
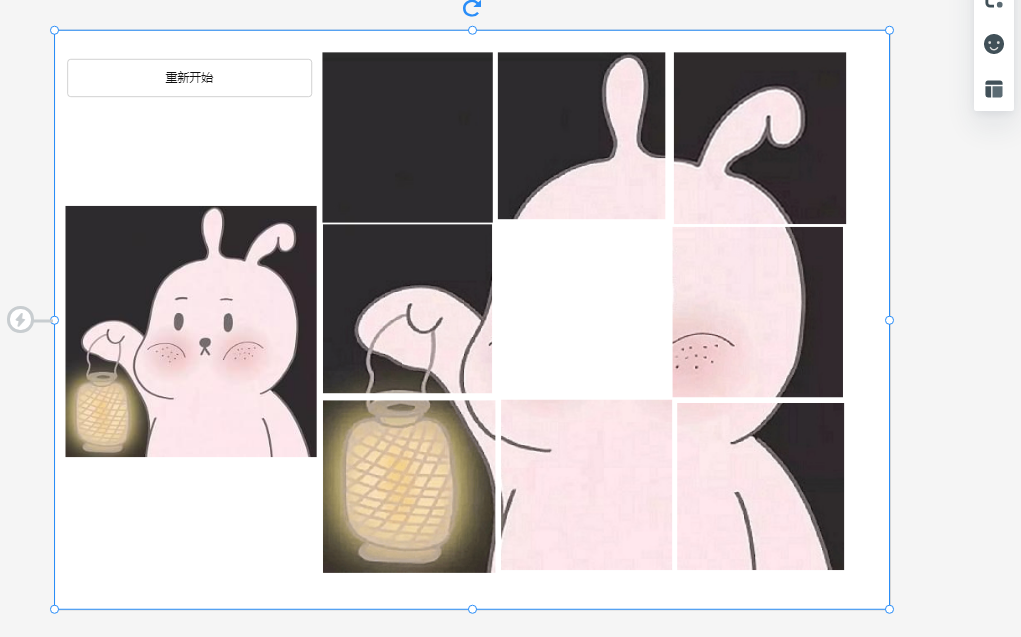

原型设计工具
- 采用墨刀
结对过程
我们宿舍其中两个人(包括我)选上了柯老板的课,所以我们俩结对就顺理成章了。

遇到的困难及解决方法
-
困难:从开源代码学习的华容道游戏发现没有初始窗口,只有直接就是拼图游戏的简陋窗口,并且窗口的大小被其固定化,若是图片分辨率不是450*450就会显示错误,且无法实现重新开始;打乱图片后可能无解,没有记录玩家每次完成后的步数及用时。
-
尝试解决: 先读懂已有的开源代码,再根据需求去学习相应的知识,不断丰富到初始代码里。
图片切割思路:
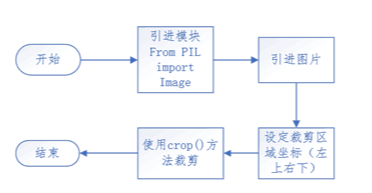
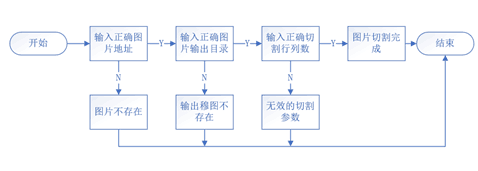
移动空白格思路:
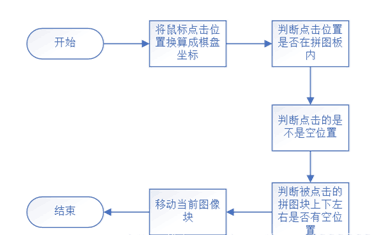
-
是否解决:不断学习丰富代码后,任何分辨率的图片都可导入游戏中,也加上了初始界面和历史记录界面,打乱图片后也保证有解。
-
收获:在各种焦头烂额之中既增加了实战经验,和队友一起熬夜(此处对应柯老板第一次博客作业说的和队友一起为项目熬夜,见识凌晨的福大)还浅浅地学了这次项目中所需要用到的各种知识。
三、AI与原型设计实现
代码实现思路
网络接口的使用
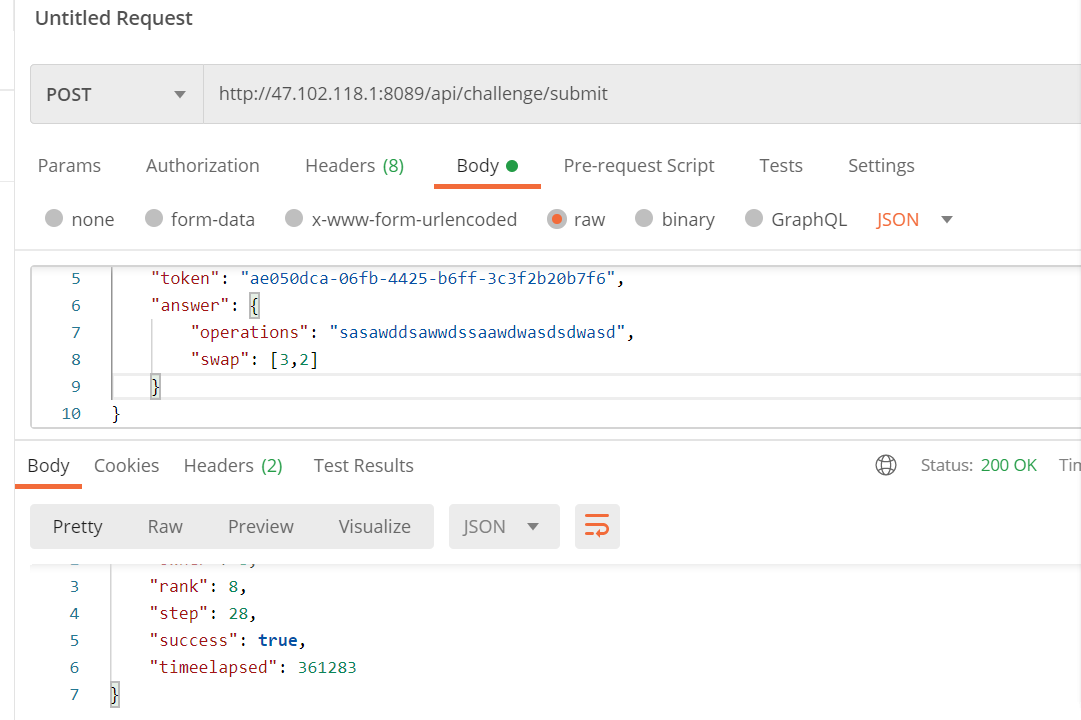
首先使用了推荐的POSTMAN用来实现网络接口的请求,例如提交答案的
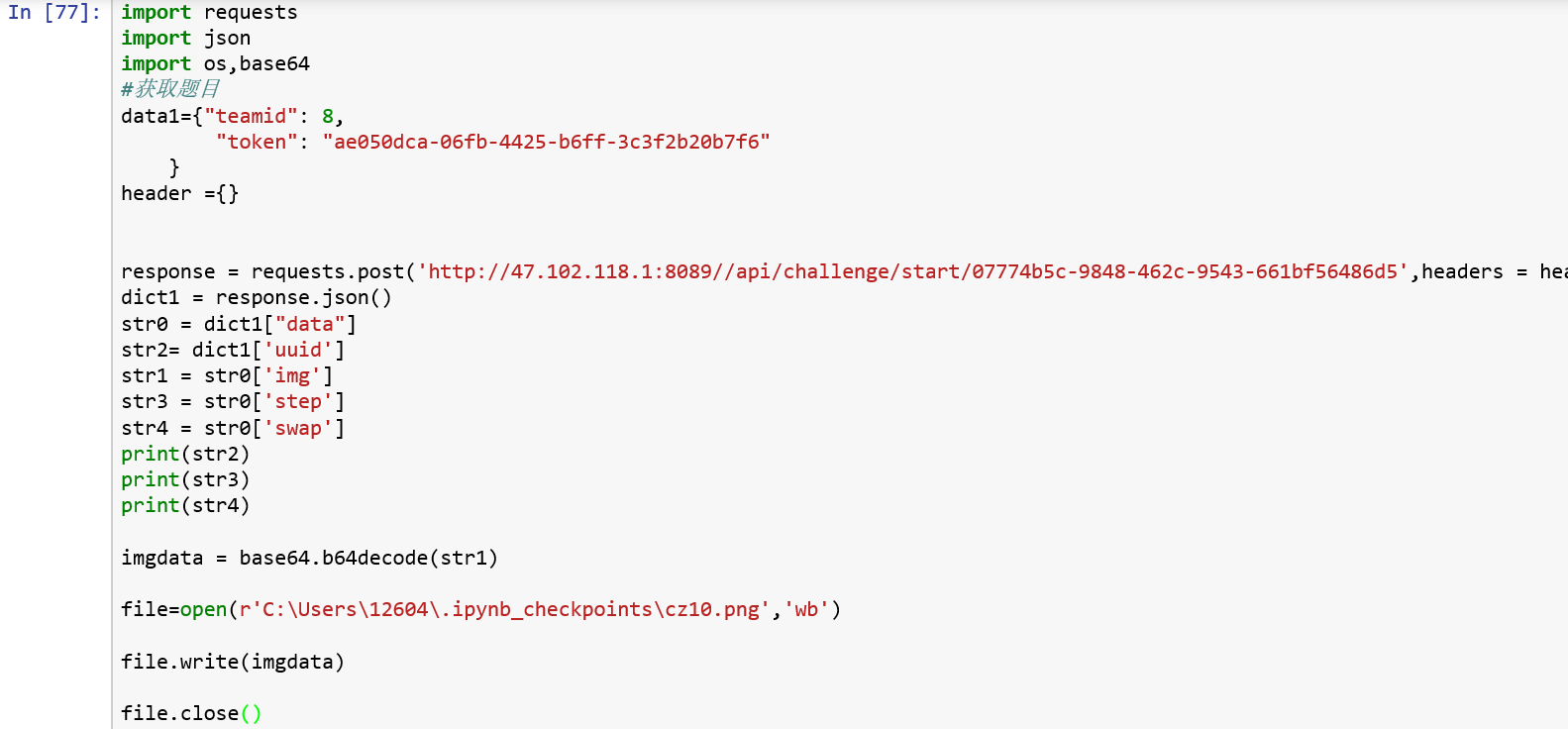
后来为了简化有效信息,用了python的request模块接受信息,只要改变所需题目的uuid就可获得答题所需信息,下载图片到指定目录
代码组织与算法关键
一般数码问题用来探究状态空间的操作序列,是人工智能最基本的形式化方法,而采用的高效解法多是两种。
A*算法
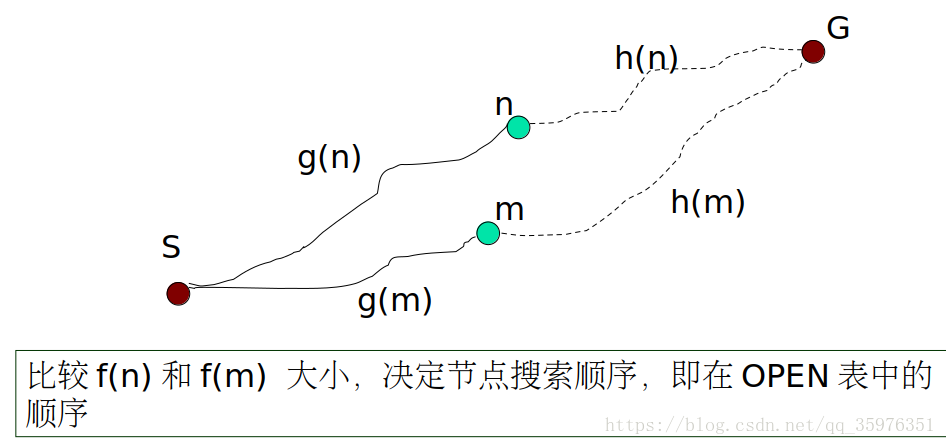
A*算法是BFS的一个变种,它把原来的BFS算法的无启发式的搜索改成了启发式的搜索,可以有效的减低节点的搜索个数。启发式的搜索公式:
f(n)=g(n)+h(n)
其中
g(n)是从根点到当前节点的距离,
h(n)是当前节点到目标节点的估计距离。
双向广搜
一般广搜从一个方向进行搜索,浪费了大量节点,双向从开始状态,进行BFS
同时,从结束状态,进行BFS
如果开始能够转成结束,那么一定存在一个中间接口状态,既在正向的BFS的队列中,又在反向的队列中
然后我们比对两种方法的结果选出最优解
流程图
A*的流程如下
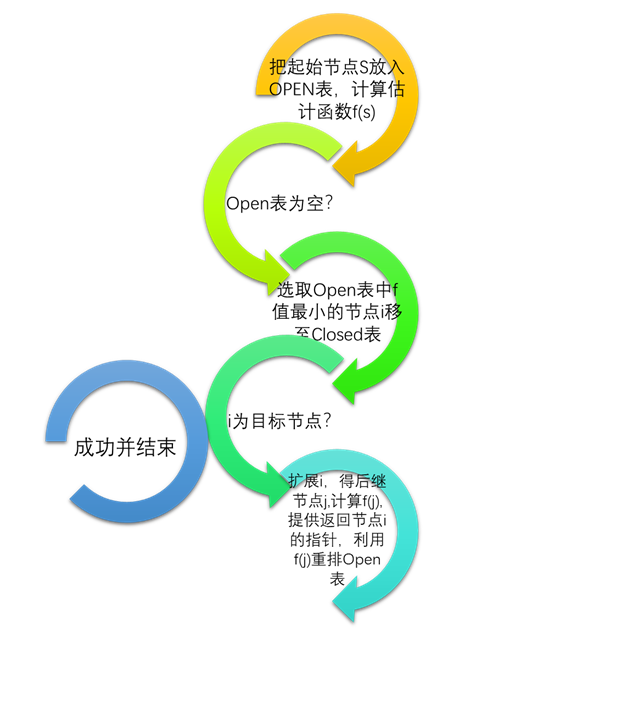
代码片段
A*
#每个位置可交换的位置集合
g_dict_shifts = {0:[1, 3], 1:[0, 2, 4], 2:[1, 5],
3:[0,4,6], 4:[1,3,5,7], 5:[2,4,8],
6:[3,7], 7:[4,6,8], 8:[5,7]}
def swap_chr(a, i, j, deep, destLayout):
if i > j:
i, j = j, i
#得到ij交换后的数组
b = a[:i] + a[j] + a[i+1:j] + a[i] + a[j+1:]
#存储fn,A*算法
fn = cal_dislocation_sum(b, destLayout)+deep
return b, fn
#返回错码和正确码距离之和
def cal_dislocation_sum(srcLayout,destLayout):
sum=0
a= srcLayout.index("0")
for i in range(0,9):
if i!=a:
sum=sum+abs(i-destLayout.index(srcLayout[i]))
return sum
def solvePuzzle_A(srcLayout, destLayout):
#先进行判断srcLayout和destLayout逆序值是否同是奇数或偶数
src=0;dest=0
for i in range(1,9):
fist=0
for j in range(0,i):
if srcLayout[j]>srcLayout[i] and srcLayout[i]!='0':#0是false,'0'才是数字
fist=fist+1
src=src+fist
for i in range(1,9):
fist=0
for j in range(0,i):
if destLayout[j]>destLayout[i] and destLayout[i]!='0':
fist=fist+1
dest=dest+fist
if (src%2)!=(dest%2):#一个奇数一个偶数,不可达
return -1, None
g_dict_layouts[srcLayout] = -1
g_dict_layouts_deep[srcLayout]= 1
g_dict_layouts_fn[srcLayout] = 1 + cal_dislocation_sum(srcLayout, destLayout)
stack_layouts = []
gn=0#深度值
stack_layouts.append(srcLayout)#当前状态存入列表
while len(stack_layouts) > 0:
curLayout = min(g_dict_layouts_fn, key=g_dict_layouts_fn.get)
del g_dict_layouts_fn[curLayout]
stack_layouts.remove(curLayout)#找到最小fn,并移除
# curLayout = stack_layouts.pop()
if curLayout == destLayout:#判断当前状态是否为目标状态
break
# 寻找0 的位置。
ind_slide = curLayout.index("0")
lst_shifts = g_dict_shifts[ind_slide]#当前可进行交换的位置集合
for nShift in lst_shifts:
newLayout, fn = swap_chr(curLayout, nShift, ind_slide, g_dict_layouts_deep[curLayout] + 1, destLayout)
if g_dict_layouts.get(newLayout) == None:#判断交换后的状态是否已经查询过
g_dict_layouts_deep[newLayout] = g_dict_layouts_deep[curLayout] + 1#存入深度
g_dict_layouts_fn[newLayout] = fn#存入fn
g_dict_layouts[newLayout] = curLayout#定义前驱结点
stack_layouts.append(newLayout)#存入集合
lst_steps = []
lst_steps.append(curLayout)
while g_dict_layouts[curLayout] != -1:#存入路径
curLayout = g_dict_layouts[curLayout]
lst_steps.append(curLayout)
lst_steps.reverse()
return 0, lst_steps
双向BFS
def do_with(cache,cache2,far,l,r,l2,r2):
flag = 0
t = cache[l]#得到所缺数字所在的行列数x,y
pos = getPos(t)
x,y = divmod(pos,3)
newpos = []
if y < 2:newpos.append(pos+1)
if y > 0:newpos.append(pos-1)
if x < 2:newpos.append(pos+3)
if x > 0:newpos.append(pos-3)
for ipos in newpos:
tt = cache[l][:]
tt[ipos]=cache[l][pos]
tt[pos]=cache[l][ipos]#如果新状态没在cache中就加入cache,队列尾巴r+1
if tt not in cache:
cache.append(tt)
far.append(l)
r += 1
#如果新状态在逆向的cache2中找到,那么新状态就是接口状态
#找到接口状态就可以直接打印了,返回接口状态的下标res,赋值给flag
res = result(tt,cache2,l2,r2)
if res != -1:
flag = res
l += 1
return cache,cache2,far,l,r,l2,r2,flag
def do_with_print(before,after):
print_after(cache,far,before)
printf_before(cache2,far2,far2[after])#如果这里不用far2[flag]而用flag就重复计算中间的接口状态
print step-1 #减去一开始的状态不计算步数
sys.exit(0)
性能分析及改进
A*
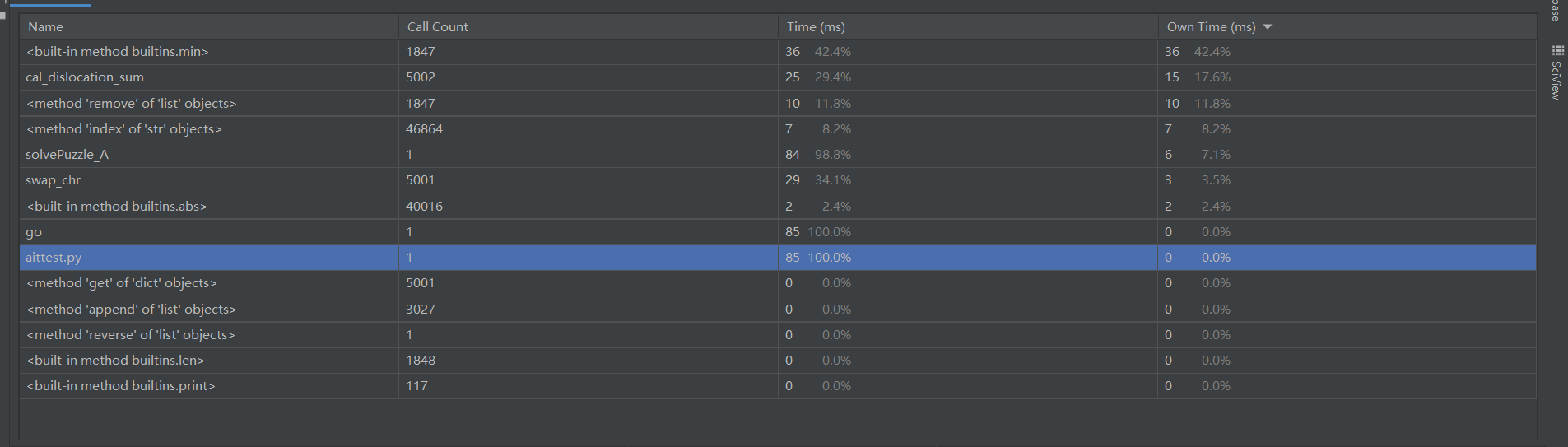
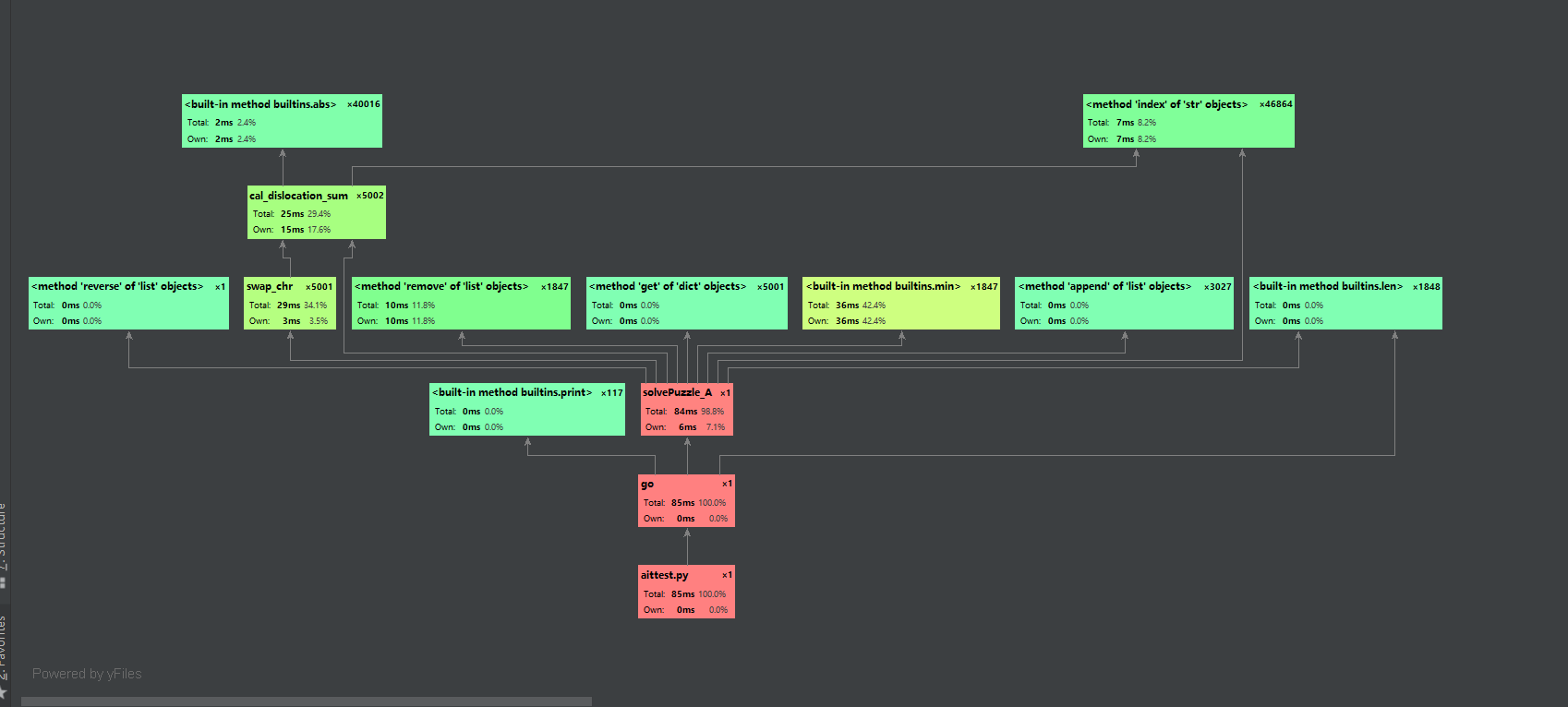
可以看到,A*的主要耗费集中在交换位置和储存上步并寻找下一步的过程上,采用列表和字典结合比较高效的提升了运行效率
双向广搜
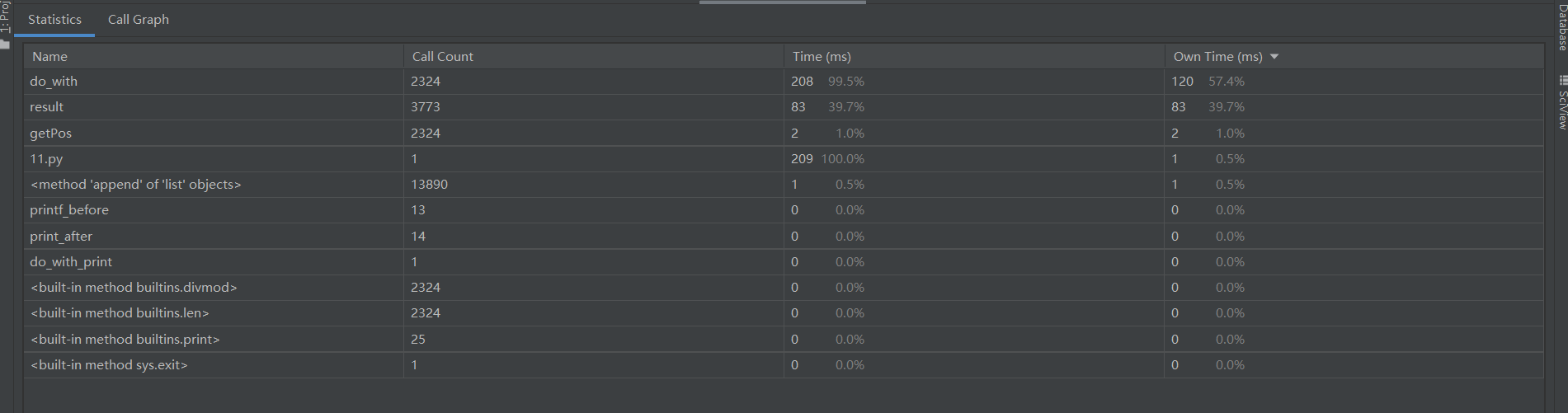
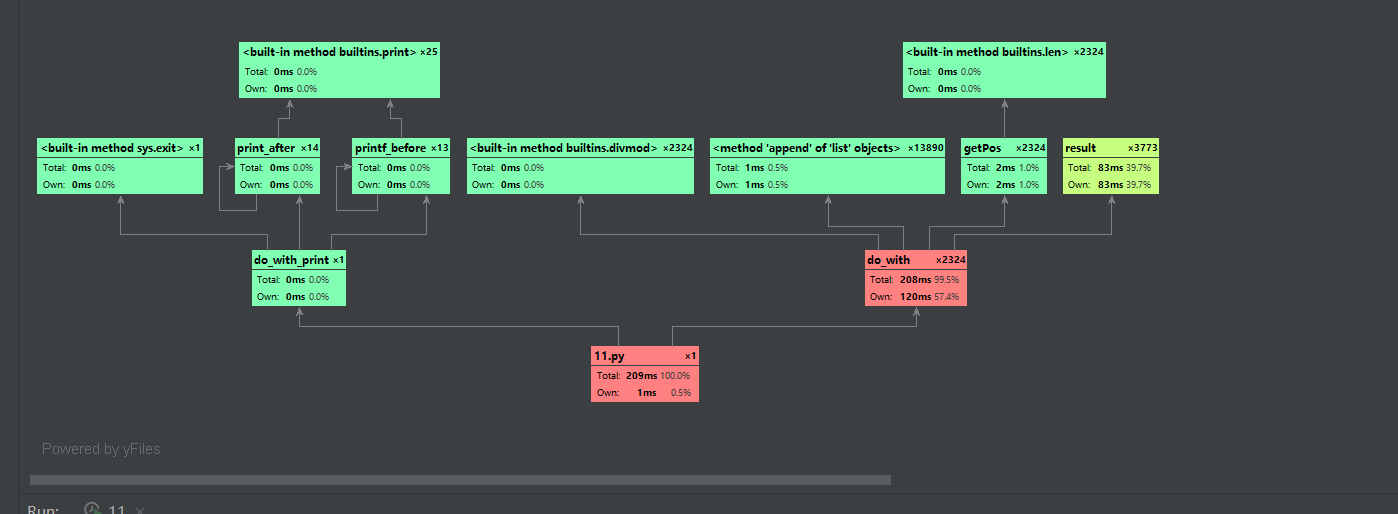
而在双向BFS,搜查下一步反而不如判断中间节点用时多,在双向同时进行时,result函数会不断判断两方能不能相遇,所以占时最多,原理如下
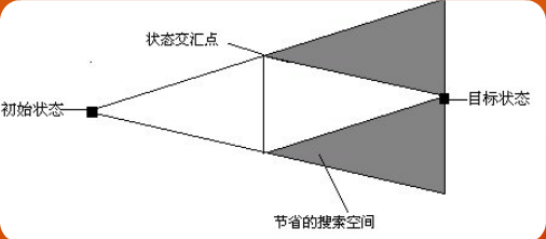
模块困难及解决
描述
题目的解决方式要求中途有强制交换后无解的情况,增加了很多限制
解决方法
我们初试的程序有判断无解的机制,但是并不会执行操作,所以我们先设置目的序列为强制交换后的序列,在指定的步数后获取相对有序的序列,再调回原有的目的序列。
这样的情况下,如果此时步数与要求强制交换的步数相等或更小,只需要自由交换原来相反的强制交换,这样恢复原序列,这样的解法是A*解法下的最优解,也确实最快步数,但是在要求步数小于所需走到打乱的目的序列的步数时,需要在调回去用程序跑,这种解法就相对不够高效。
评价队友
李赫同学遇事沉着冷静,不慌不忙,还经常鼓励我,让我备受鼓舞!
学习进度
| 第N周 | 新增代码(行) | 累计代码(行) | 本周学习耗时(小时) | 累计学习耗时(小时) | 重要成长 |
|---|---|---|---|---|---|
| 1 | 146 | 146 | 10 | 10 | 设计原型,学习了py有关的opencv、Image、ImageTK等图形库,掌握图片切割以及对比的方法 |
| 2 | 127 | 273 | 12 | 22 | 学习了用ImageTK生成窗口,并进行按钮嵌入和一定程度的排版美化 |
| 3 | 62 | 335 | 7 | 29 | 初步完成了游戏的雏形,能够生成初始窗口和子窗口 |
| 4 | 73 | 408 | 5 | 34 | 能够保存每一次成功的游戏数据并显示在子窗口中 |
PSP
| PSP | Personal Software Process Stages | 预估时间/分 | 实际时间/分 |
|---|---|---|---|
| Planning | 计划 | 600 | 450 |
| Estimate | 预计时间 | 450 | 420 |
| Development | 开发 | 1200 | 1800 |
| Analysis | 需求分析 | 30 | 60 |
| Design Spec | 生成文档 | 100 | 100 |
| Design Review | 复视 | 20 | 30 |
| Coding Standard | 标准 | 10 | 10 |
| Design | 设计 | 660 | 800 |
| Coding | 编码 | 340 | 200 |
| Code Review | 检查 | 10 | 10 |
| Test | 测试 | 30 | 60 |
| Reporting | 报告 | 60 | 60 |
| Test Report | 测试报告 | 30 | 30 |
| Size Measurement | 工作量 | 20 | 20 |
| Postmortem & Process Improvement Plan | 总结 | 60 | 60 |
| --- | 合计 | 3620 | 4110 |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号