线性代数前情提要

个人理解：线性代数所用工具是数学化的公式表达，但它是有实际和几何意义的，比如矩阵只是空间的变换，任何一个矩阵都是对空间的变换或压缩。

线性变换：以基向量为基础（有几个不同类型的基向量，就代表着表示的是几维空间，比如用i和j两个基向量，表示二维空间中的向量变换，而i、j和z可以表示三维空间向量，以此类推），其它任意向量都能表示为基向量的线性组合。

以下是观看3Blue1Brown视频的总结（个人认为比较重要的内容）

1、线性变换及矩阵向量乘法的实际意义

 

 

 

 

 

 

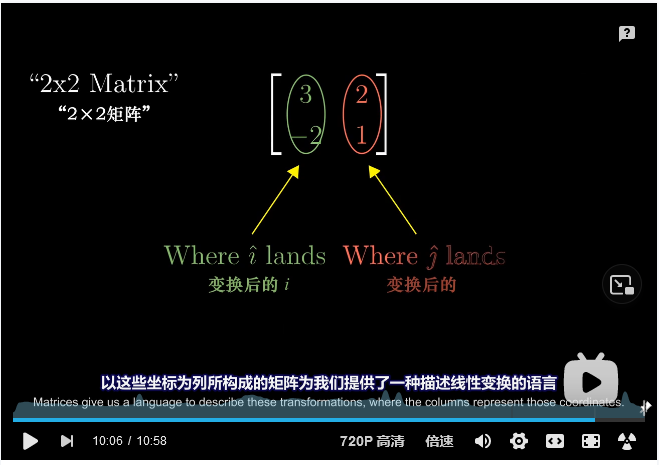
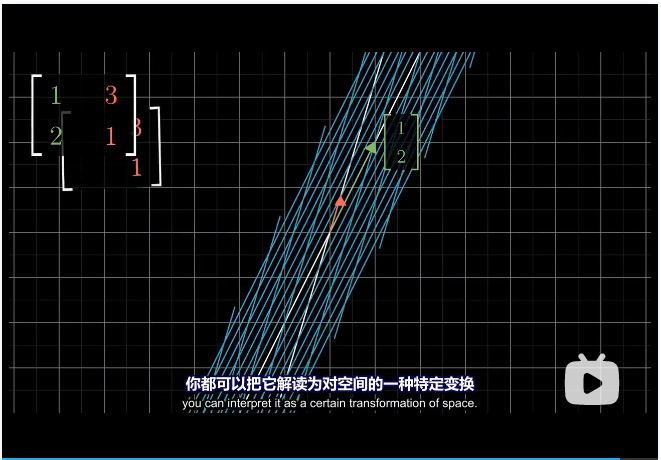
***每当你看到一个矩阵时，你都可以把它解读为对空间的一种特定变换

 

 2、线性的定义：

 

 3、矩阵乘法与线性变换复合

 

 

 

 

 

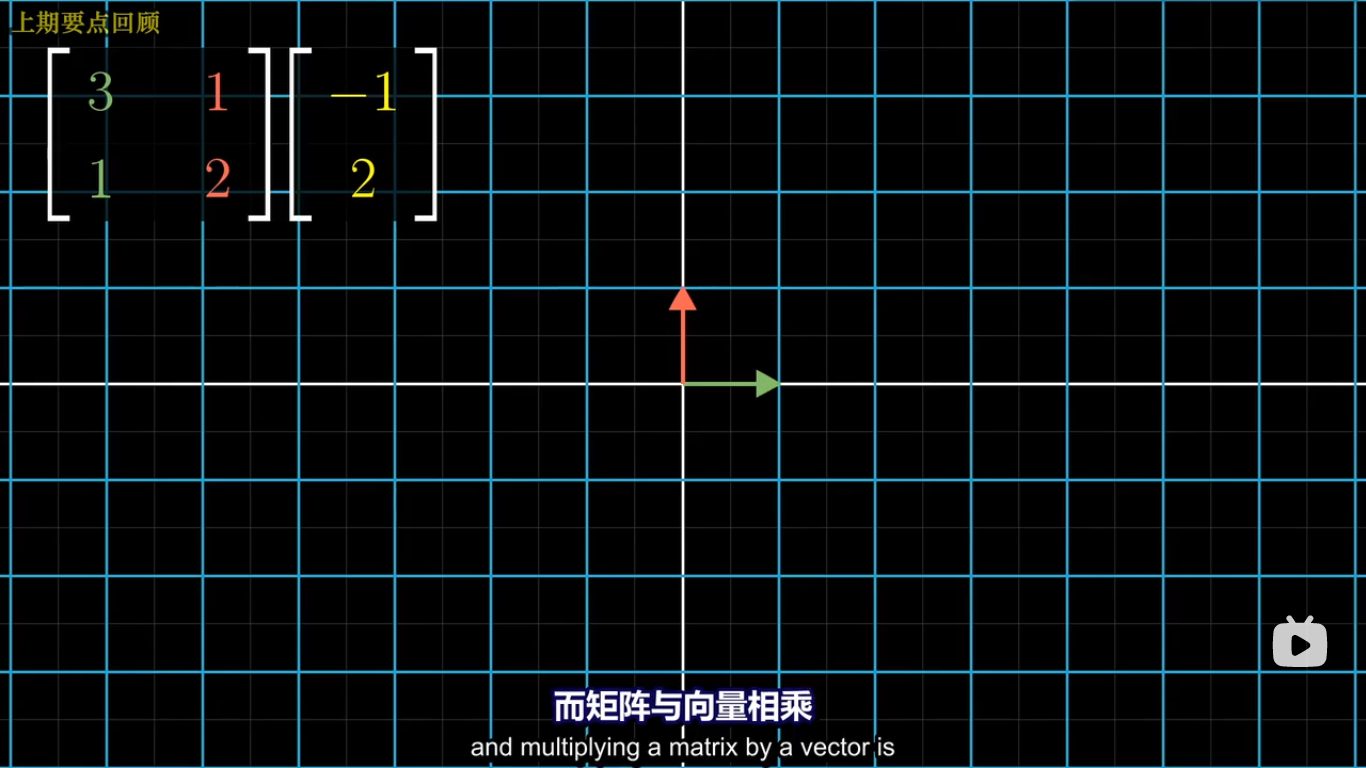
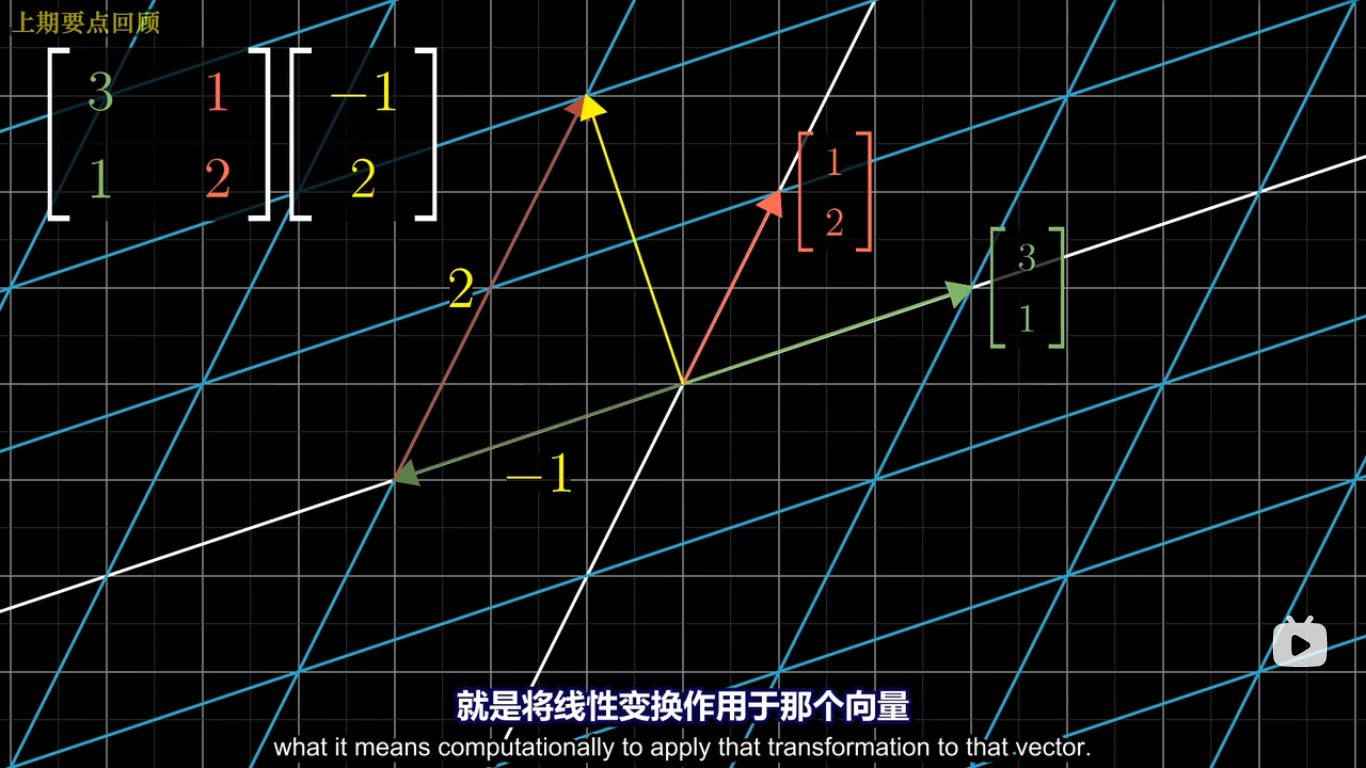
 如果你有一个向量，将它进行旋转然后剪切，一个麻烦的计算方法是：首先将它左乘旋转矩阵，然后将得到的结果再左乘剪切矩阵

 

 

 

 

 

 

 

 

 

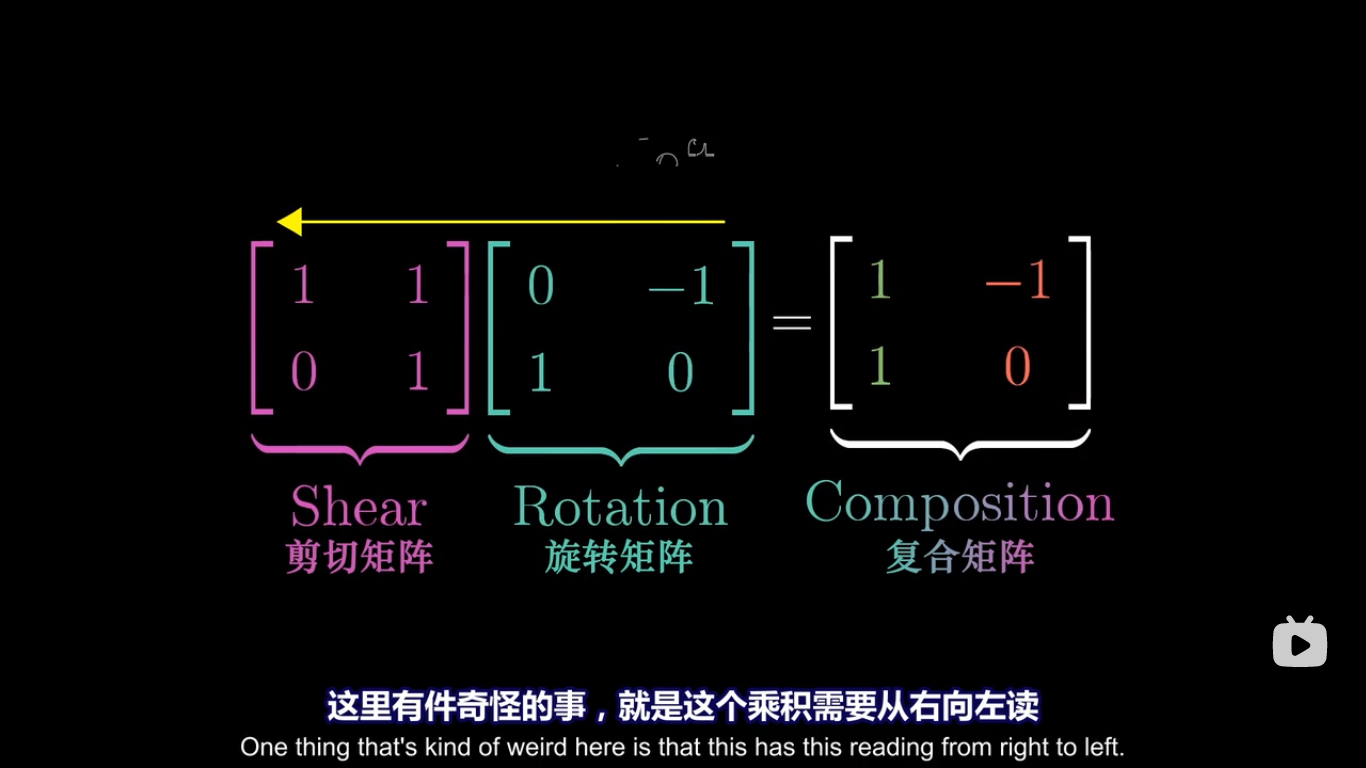
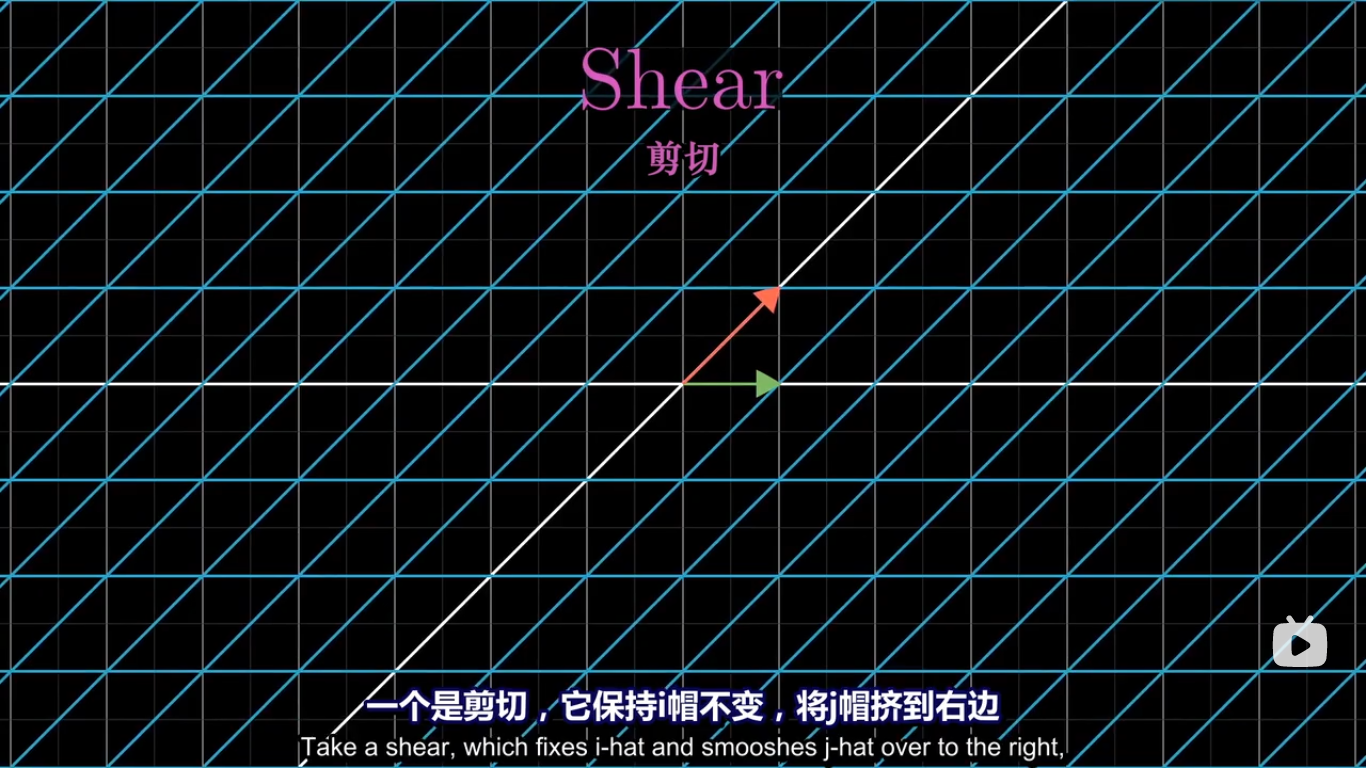
 剪切矩阵：

 

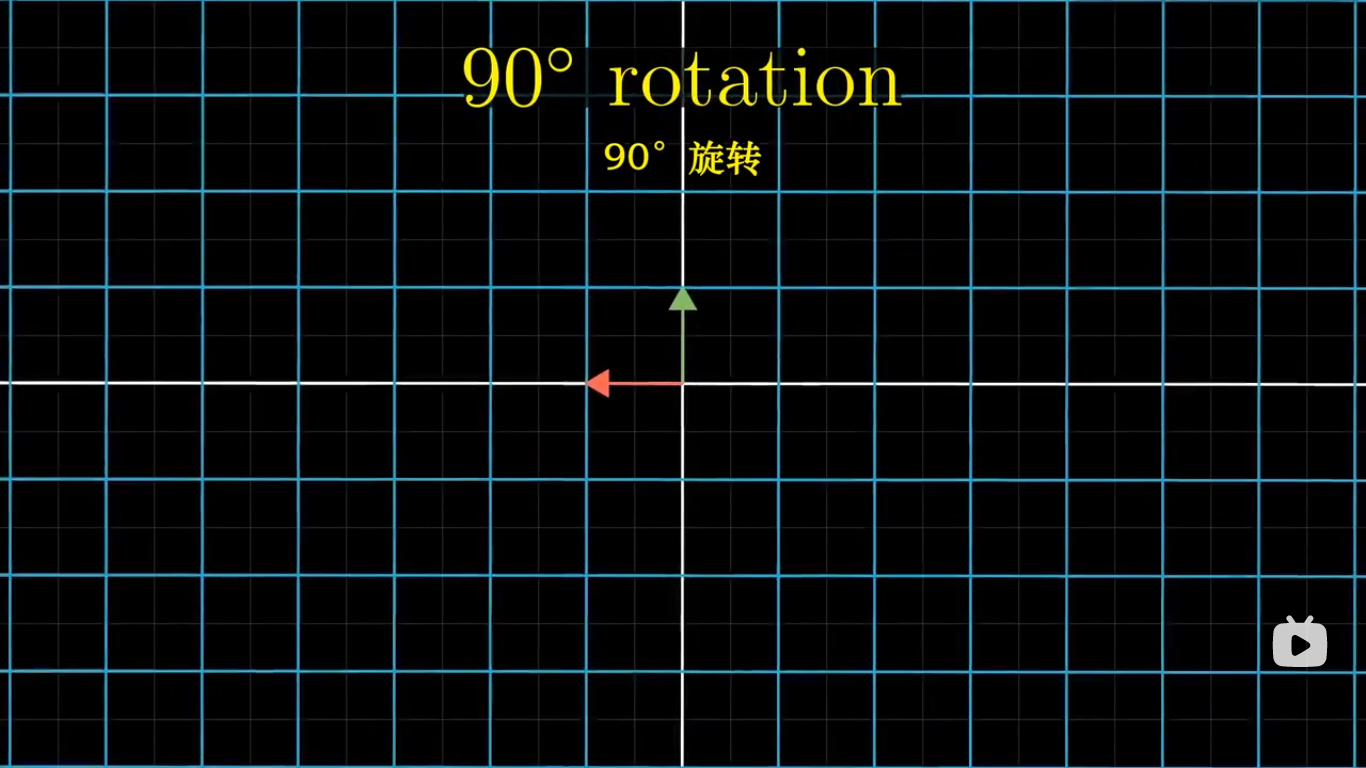
 旋转矩阵：