Clustering-based genetic offspring generation for solving multi-objective optimization problems with intricate Pareto sets
普通的SBX

存在的问题:
我们以ZDT1问题为例子
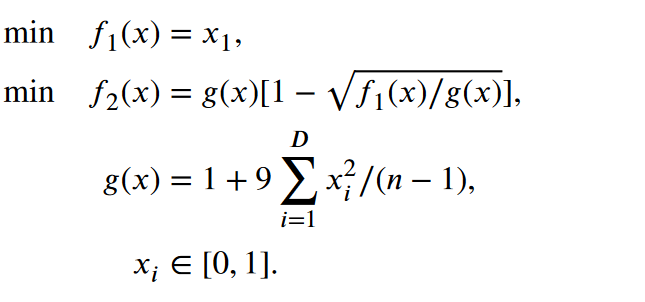
其真实的PS(Pareto-optimal set)𝑥1 ∈ [0, 1] and 𝑥𝑖 = 0 for 𝑖 = 2, ... , 𝐷。这表明PS和决策变量是平行的。
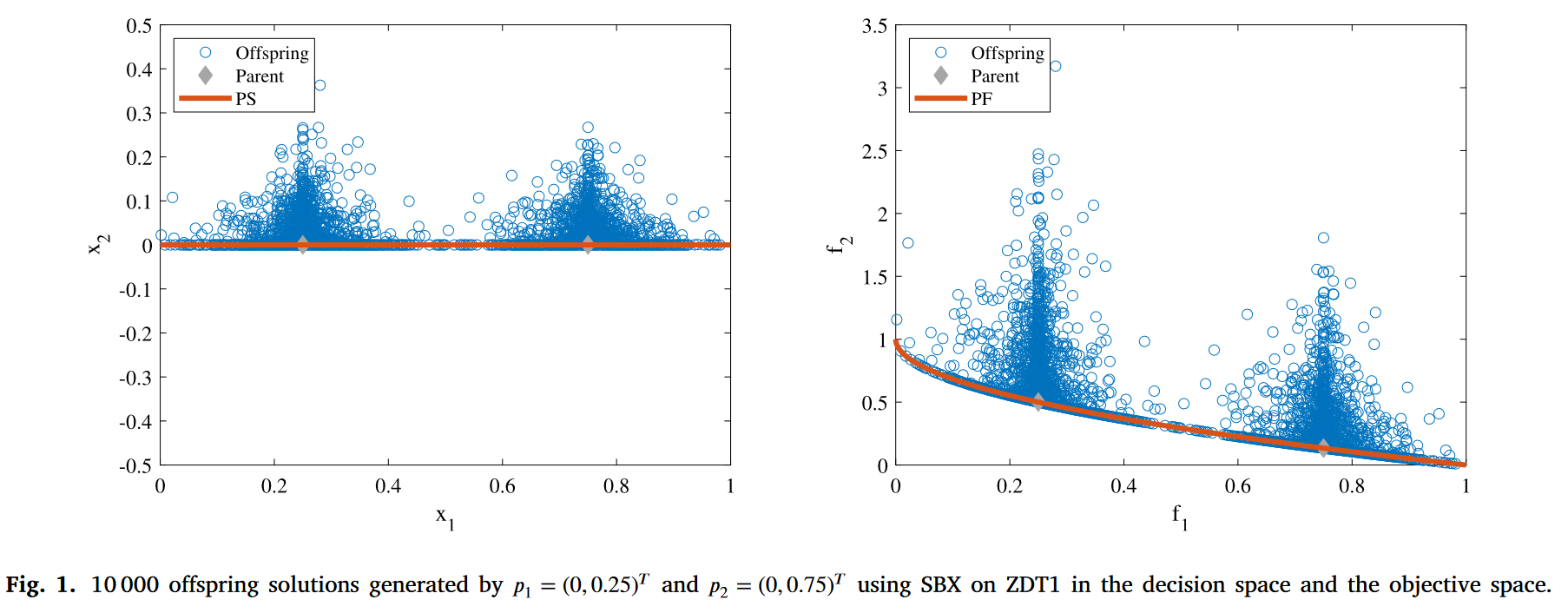
如上图所示PS和x1平行。所以这种情况下SBX有很好的效果。
但是实际上真实的PS并不一定是平行于决策变量的。
例如ZDT1函数的变体RM1
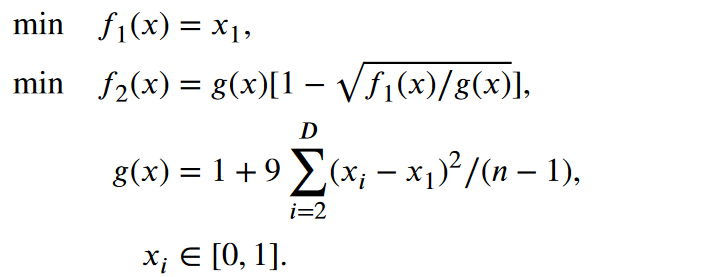
在Rm1中,当i= 2,..,D时,PS为x1∈[ 0、1 ],xi = x1。
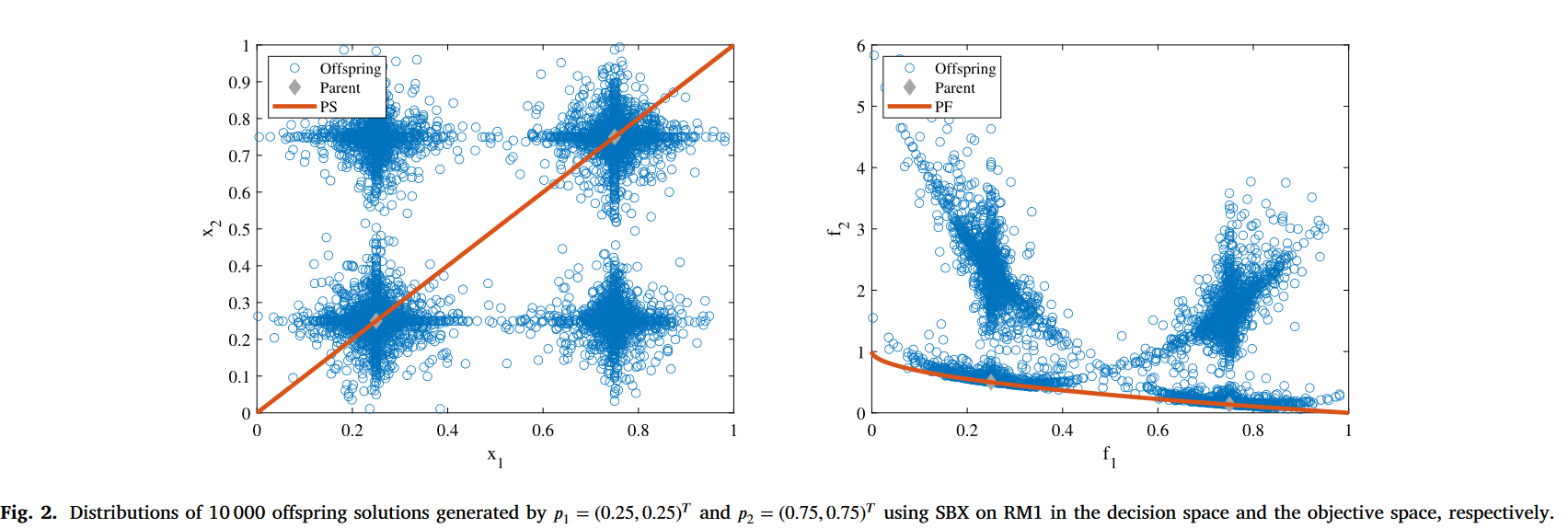
如上图所示,PS不在是和决策变量平行状态,而是旋转。这个时候再使用
SBX就会得到的子代显然很差。
注以fig1,2中的p1(0.25,0.25),p2(0.75,0.75)
改进的RSBX
基于旋转的SBX ( RSBX )的新方法来处理旋转的MOPs。其核心原理是利用一个旋转矩阵V来操纵搜索空间内的个体。旋转矩阵的构建依赖于当前种群导出的协方差矩阵。
1.繁殖过程开始于计算当前种群的平均向量m,如( 4 )所示。

2.随后,协方差矩阵C由( 5 )式计算,其中xi表示第i个个体的决策变量的向量,xi,k和mk分别表示xi和m的第k个元素。
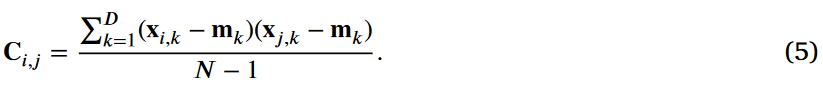
3.然后利用特征分解通过式( 6 )确定C (式中: vi为第i个最大特征值λ i)的特征向量v1,..,vD。

4.D个独立的特征向量作为决策空间的基,矩阵V ( V∈RD × D)作为旋转矩阵。在种群旋转后,利用SBX生成子代解,然后利用式( 7 )将子代解旋转回父代的方向。

存在的问题
显然RSBX在处理线性PS上是具有可取之处的,但是实际问题的PS并不一定总是呈线性的。在非线性PS的问题RSBX又会陷入窘境。
如图:
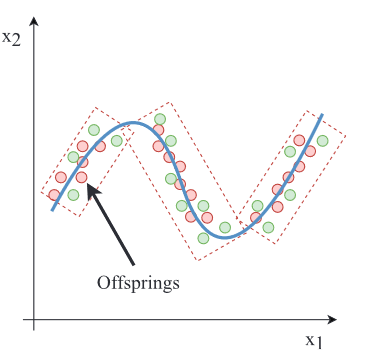
这种非线性的PS显然不是那么容易提取出它的方向矩阵。
CRSBX(基于聚类的自适应RSBX)
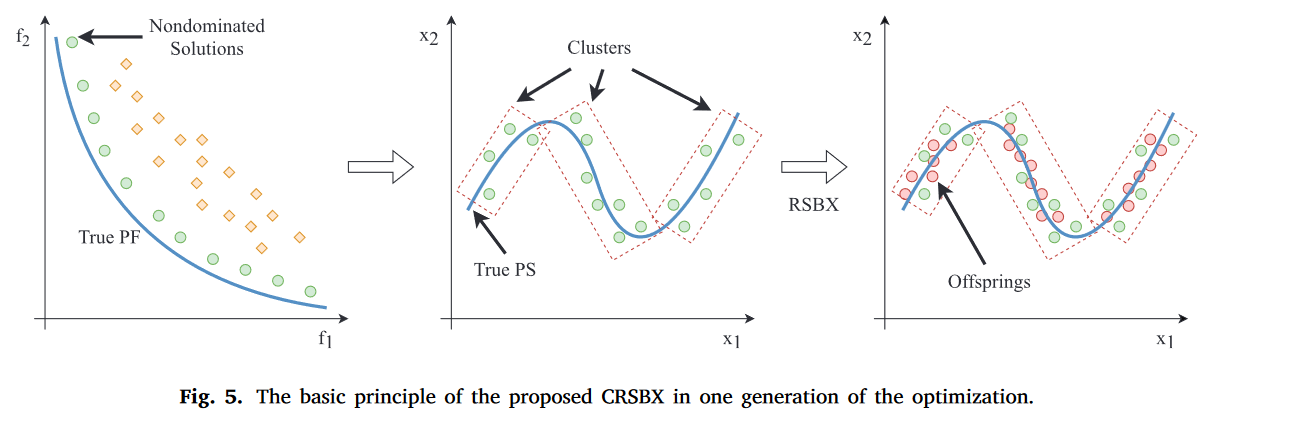
如图,将非线性的PS分解成N段线性部分。
在进化出足够多的世代之前,种群还没有探索到PS附近的区域,这可能会导致聚类的潜在不准确性。因此,ARSBX被用来解决这个问题。相比之下,在搜索后期使用了基于聚类的后代生成策略,进行了更全面的探索。通过采用这两个阶段的方法,CRSBX旨在利用每个方法在搜索过程的不同阶段的优势
算法1

算法2

Ps参数设置
sigmod函数

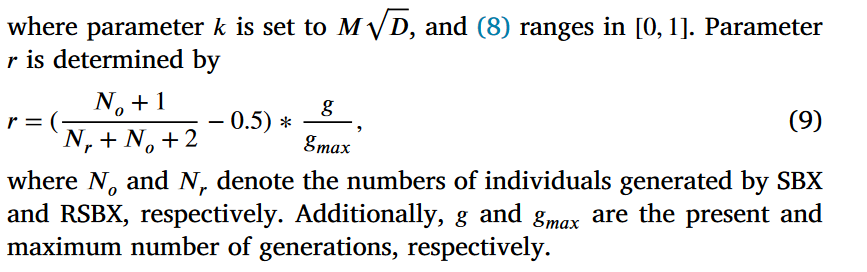



 浙公网安备 33010602011771号
浙公网安备 33010602011771号