LMOCSO

Efficient Large-Scale Multiobjective Optimization Based on a Competitive Swarm Optimizer

原始的CSO

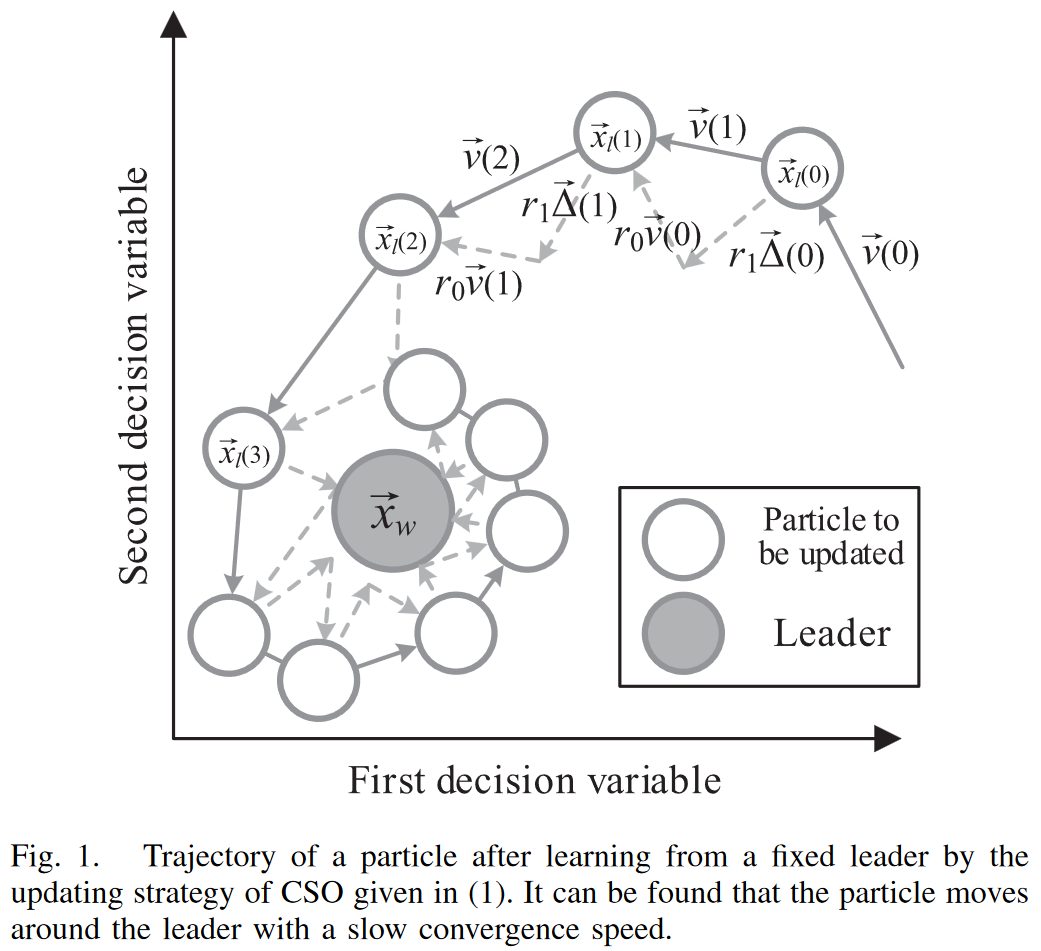
\(\vec{x_w}\) 是引导粒子，\(\vec{x_l} , \vec{v_l}\)分别是待更新粒子和其更新的速度方向。\(R_0,R_1\)是在[0,1]的均匀随机分布。

通过图中的引导线可以知道粒子向更优解的更新速度很慢。

LMOCSO改进的CSO

从当前种群随机选取两个粒子，\(\vec{x_l}\vec{x_w}\),根据之前的速度更新位置。

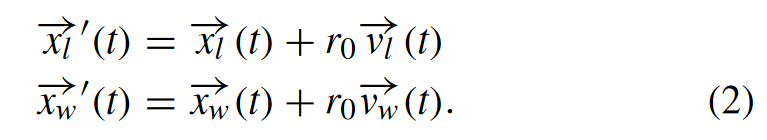
然后适应度值差的粒子 \(\vec{x_l}\) 会向 \(\vec{x_w}\) 优化：

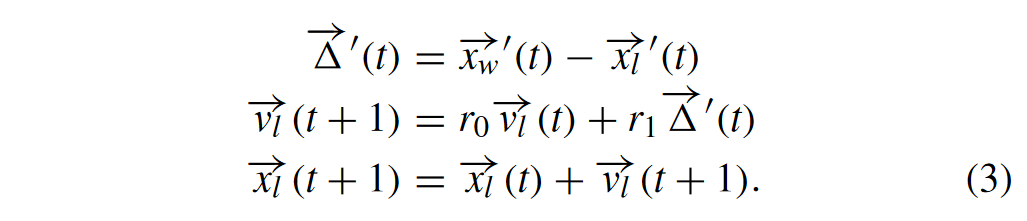
值得考虑的是经过公式（2）的改变，决策变量 \(\vec{x_l'}\) \(\vec{x_w'}\) 的适应度值的优劣性可能会反过来，所以这时候就需要额外的FE开销去评估这两个粒子。作者为了避免花费过多的FE去评价更新的粒子这种情况于是将公式（2）（3）转化成如下的形式。

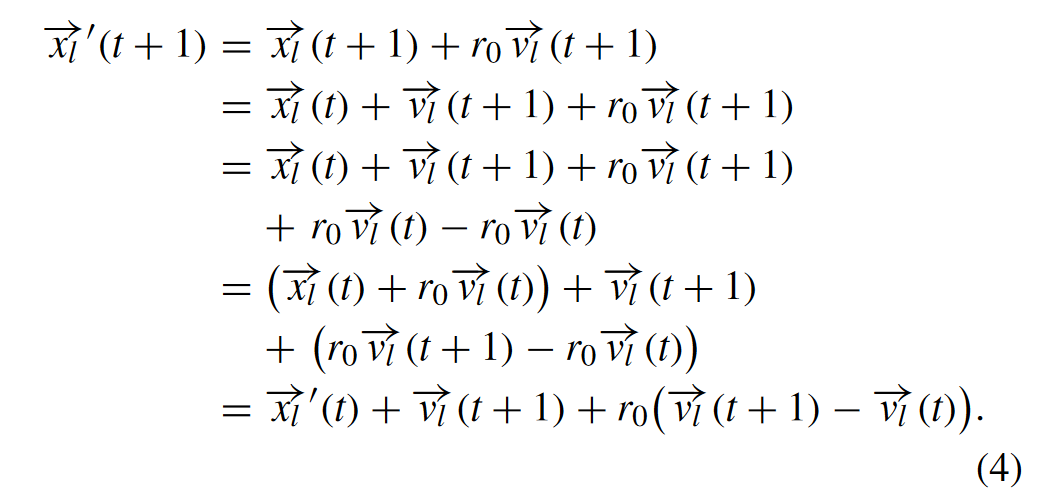
于是有了：

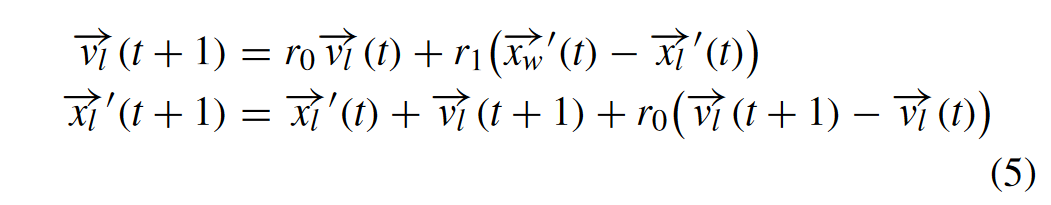
这样公式（5）就消去了 \(\vec{x_l}\) 只包含 \(\vec{x_l'}\),于是我们就可以通过 \(\vec{x_l}(t-1)\) 直接得到 \(\vec{x_l'}\)，这样就直接跳过了 \(\vec{x_l}\) 不用花费额外的FE去评价 \(\vec{x_l}\) 节约了FE。

shift-based density estimation (SDE) strategy

粒子 p 的适应度定义为该粒子与种群中其他粒子之间基于 SDE 的最小距离。

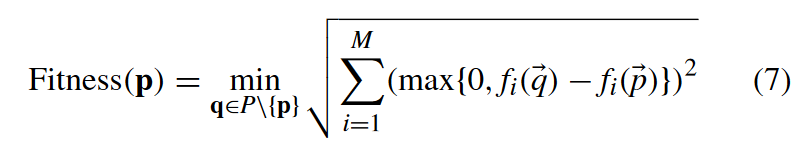
其中 fi（ p） 表示 p 的第i 个目标值，M 表示目标的数量。SDE 策略可以从收敛性和多样性两个方面评估解决方案的质量。

代码如下：
function Fitness = calFitness(PopObj)
    % Calculate the fitness by shift-based density

    N      = size(PopObj,1);
    fmax   = max(PopObj,[],1);
    fmin   = min(PopObj,[],1);
    PopObj = (PopObj-repmat(fmin,N,1))./repmat(fmax-fmin,N,1);
    Dis    = inf(N);
    for i = 1 : N
        SPopObj = max(PopObj,repmat(PopObj(i,:),N,1));
        for j = [1:i-1,i+1:N]
            Dis(i,j) = norm(PopObj(i,:)-SPopObj(j,:));
        end
    end
    Fitness = min(Dis,[],2);
end