Dual Differential Grouping: A More General Decomposition Method for Large-Scale Optimization

Dual Differential Grouping: A More General Decomposition Method for Large-Scale Optimization

可分离定义和DG

Definition 1：

当且仅当函数\(f (x)\)具有k个独立分量时，对于最小化是部分可分离的:

Definition 2:

函数\(f\)是部分可加可分的，如果它具有以下形式:

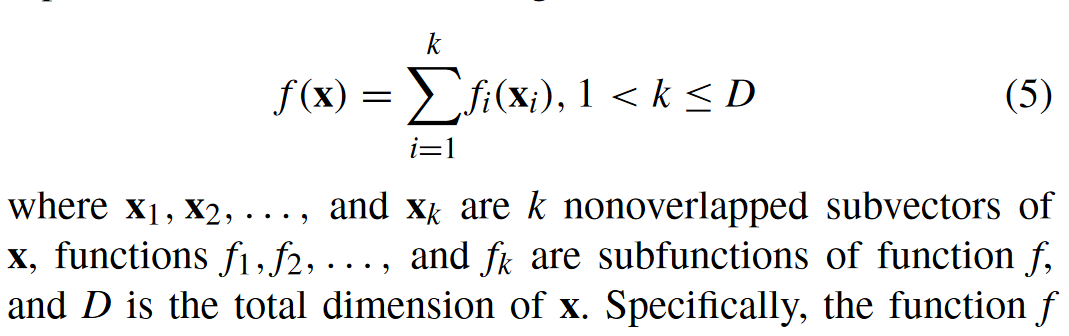
DG的定理

Proposed DDG

Multiplicatively Separable Function(可乘性可分离函数)：

一个函数\(g\)如果是下列形式，就说明这函数是部分乘法可分离：

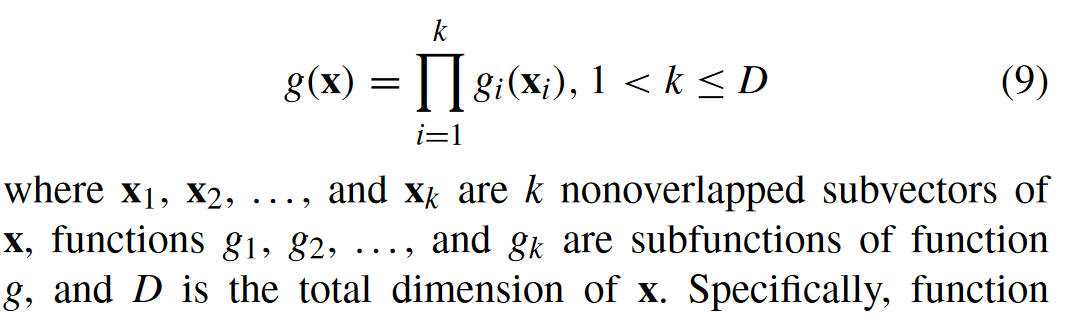
如过 K=D 那么这就是完全可分离，如果 K=1，那么就是完全不可分离。

定理 2：每一个加法可分离函数可以转换为乘法可分离函数。

定理 3：凡最小值大于0的乘性可分离函数都可以转化为可加性可分离函数。

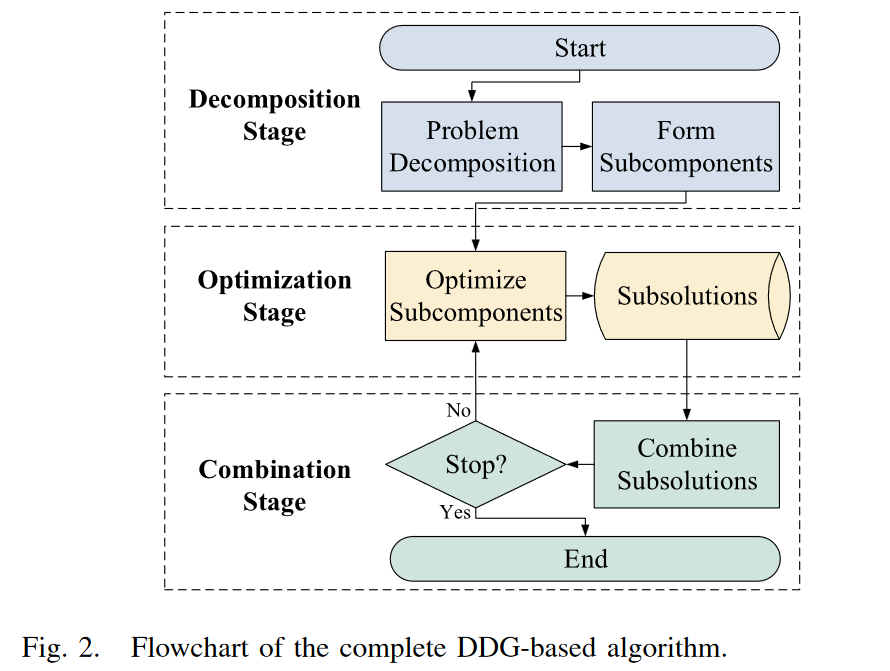
算法分析

algorithm 1

如果tempgroup长度==1，也就是说明i是可分离变量，将其放进seps的集合中{{i},{}},如果不可分离，将和i不可分离的变量j,k,l...放入集合allgroups={{i，j,k,l,...},{}}中。dims去掉已经处理的变量下标，继续算法1.

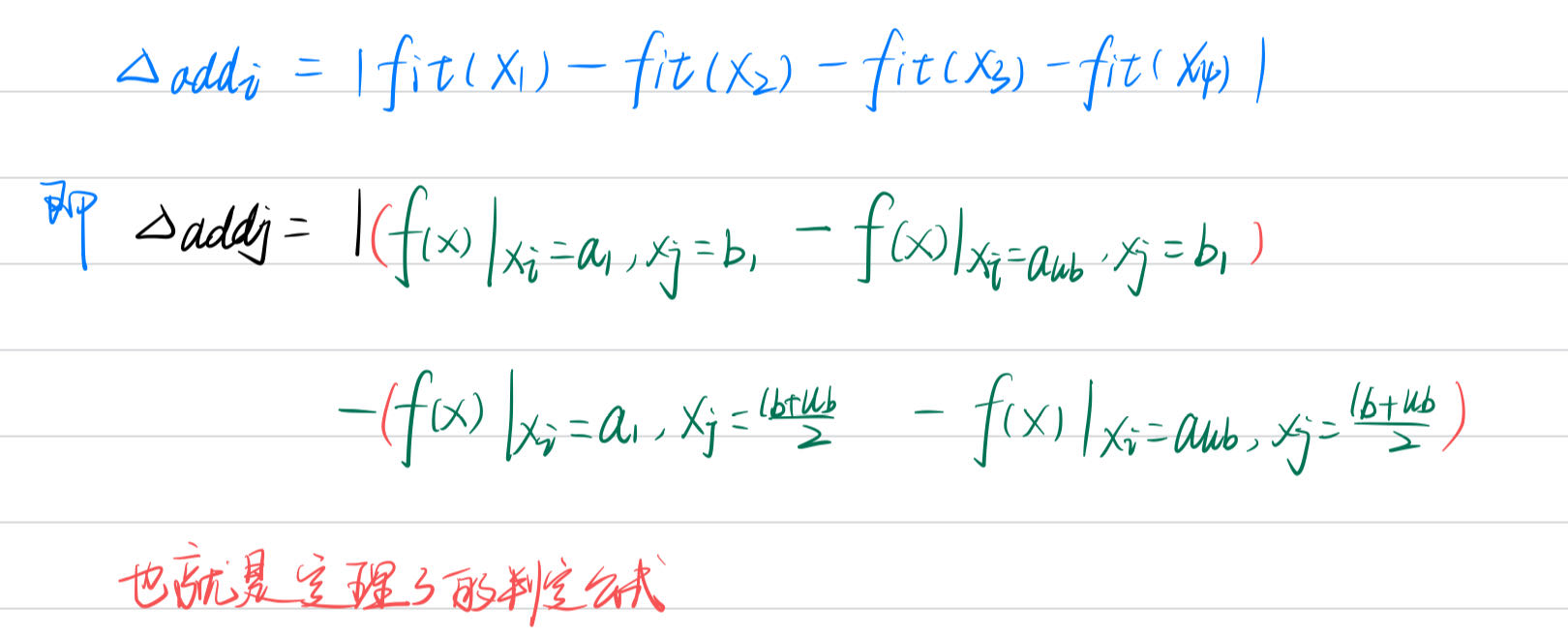
algorithm 2

主要部分 ：
line 13 :拿到分组后每一组的变量下标

line 14: 根据下标可以分成不同的优化子问题（可以参考MOEA/DVA的subcomponent，我是这么觉得）

line 15-18: 利用优化算法优化子问题得到子部件最新的变量值

line 19: 计算新的fitness

line 20: 保留最好的解

Case Study on the Parameter Optimization for Neural Network-Based Application

训练损失（Training Loss）是在训练神经网络模型期间使用训练数据计算出的损失值。它是模型在当前训练数据上的性能度量，表示模型预测与训练数据真实标签之间的差异或误差程度。

通常情况下，训练损失是通过某种损失函数（也称为代价函数或目标函数）来计算的，这个函数根据模型的预测输出和真实标签之间的差异来度量损失。常见的损失函数包括均方误差（Mean Squared Error，MSE）、交叉熵损失（Cross-Entropy Loss）等。

在训练过程中，模型的目标是最小化训练损失，即使得模型在训练数据上的预测尽可能接近真实标签。通过反向传播算法和优化算法（如梯度下降法），模型会根据训练损失的梯度调整模型参数，以使训练损失逐步减小，从而提升模型的性能。

训练损失是监督学习任务中的一个重要指标，它可以帮助我们了解模型在训练数据上的表现，并且在模型训练过程中可以用来监控模型的收敛情况和训练进度。