A Framework for Large-scale Multi-objective Optimization based on Problem Transformation
作者提出了一种新的优化框架,称为加权优化框架(WOF),该框架基于问题转换、优化多个权重向量和变量分组。
Cooperative Coevolution(协同进化的基本原理和概念)
Cooperative Coevolution(协同进化)是一种进化算法,用于解决复杂的优化问题,尤其是那些具有高维度、非凸性、非线性、离散性或不可导性质的问题。它将问题分解成多个子问题,并采用多个进化群体分别优化每个子问题,然后通过协同合作来组合子问题的解以获得整体解。
以下是Cooperative Coevolution的基本原理和概念:
-
问题分解(Decomposition): 将复杂的优化问题分解成多个相对简单的子问题。通常,问题的分解可以根据问题的结构、特性或者先验知识来进行,每个子问题可能只涉及到问题的一部分变量或特征。
-
多群体进化(Multi-population Evolution): 对每个子问题分别建立一个进化群体,通过进化算法(如遗传算法、粒子群优化等)来优化子问题的解。每个群体独立地进行进化,并尝试寻找最佳的解决方案。
-
协同合作(Cooperation): 不同的子问题可能相互关联或者依赖,因此需要一种机制来协调不同群体之间的合作。在Cooperative Coevolution中,通常采用合作方案来交换信息、共享资源或者协调搜索方向,以促进全局最优解的发现。
-
解的组合(Solution Combination): 一旦每个子问题的最优解被找到,需要将这些局部最优解组合成整体解。这可以通过简单的组合规则来完成,例如将每个子问题的最优解直接组合在一起,或者根据一定的权重进行线性或非线性组合。
-
性能评估与适应度计算(Performance Evaluation and Fitness Calculation): 在Cooperative Coevolution中,需要设计适应于分解问题的适应度函数,以评估每个子问题的性能,并指导进化过程。通常,适应度函数会考虑子问题的局部最优解以及子问题之间的协同合作。
Cooperative Coevolution的主要优势在于它能够处理复杂的高维度优化问题,并通过有效的问题分解和协同合作来加速搜索过程,避免陷入局部最优解。这种方法已经被广泛应用于许多领域,如工程优化、机器学习、模式识别等。然而,设计合适的问题分解策略和合作机制仍然是Cooperative Coevolution研究的关键挑战之一。
Differential Grouping (DG)的基本原理和思想
Differential Grouping (DG) 是一种用于解决复杂优化问题的进化计算技术。它是协作协同进化算法的一种变体,旨在解决具有高维度、多模态或非线性的优化问题。
DG 算法的基本原理和思想如下:
-
群体分组: 首先,将优化问题中的参数空间分成多个组(groups),每个组中包含若干个参数。这种分组可以基于特征、问题的结构、参数之间的相关性等因素进行。
-
差分进化: 在每个组内部,使用差分进化(Differential Evolution,DE)等进化算法来进行局部优化。DE 是一种基于群体搜索的优化算法,通过利用种群中个体之间的差异来搜索解空间。
-
信息交流: 不同组之间通过某种信息交流机制来协作,以共同优化整个问题。这种信息交流可以是参数的交换、组内最优解的共享,或者其他形式的协作。
-
适应度评估: 对每个组内的个体进行适应度评估,衡量其在解决子问题中的优劣程度。适应度函数可以根据具体问题而定,通常用于评估个体的解的质量。
-
更新策略: 根据适应度评估结果,采用合适的更新策略来更新每个组内的个体。更新策略通常包括选择操作、交叉操作和变异操作等。
通过将参数空间分成多个组,并在每个组内使用差分进化等局部优化算法进行搜索,DG 算法可以更有效地处理高维度、多模态或非线性的优化问题。同时,通过不同组之间的信息交流和协作,可以在全局范围内搜索更优的解,从而提高了算法的全局搜索能力和收敛速度。
总之,Differential Grouping (DG) 算法是一种利用群体分组和差分进化进行协作的优化技术,适用于解决复杂优化问题。其核心思想是将大问题分解为小问题,并通过信息交流和协作来达到全局优化的目标。
差分进化
差分进化(Differential Evolution,DE)是一种优化算法,通常用于解决连续参数优化问题。它是一种进化算法,灵感来源于自然界中的生物进化过程,特别是基因组合和自然选择。
差分进化算法的基本原理如下:
-
个体表示: 在差分进化算法中,问题的解被称为个体(individual),通常用一个实数向量来表示。每个个体对应于问题的一个候选解,向量的每个元素代表解空间中的一个参数。
-
初始化种群: 首先,随机生成一组个体作为初始种群,这些个体在解空间中是均匀分布的。
-
变异操作: 差分进化算法通过变异操作来产生新的解。在变异操作中,选择种群中的三个个体(通常称为基向量)作为参考,然后利用它们的差异来生成新的解。常见的变异操作是基于向量差的线性组合,公式如下:
对于第 \(i\) 个个体 \(x_i\),选择三个不同的个体 \((x_r, x_s, x_t) r, s, t\) 都不等于 \(i\),然后计算变异个体 \(v_i\):
$ v_i = x_r + F \cdot (x_s - x_t) $
其中 \(F\) 是变异因子,用于控制变异程度。
-
交叉操作: 生成变异个体后,通过交叉操作将变异个体与原个体进行组合,以产生子代个体。交叉操作控制了新个体与原个体之间的关系,通常采用二项式分布或指数分布来确定交叉概率。
-
选择操作: 将新生成的子代个体与原个体进行比较,保留适应度更好的个体作为下一代种群。这里的适应度评价是根据问题的目标函数计算的。
-
重复迭代: 重复进行变异、交叉和选择操作,直到达到终止条件。终止条件可以是达到最大迭代次数、目标函数值收敛到一定阈值等。
差分进化算法具有较好的全局搜索能力和鲁棒性,适用于解决各种类型的优化问题,特别是那些非线性、非凸、多峰和高维的问题。它在许多领域中都有广泛的应用,如工程优化、机器学习、信号处理等。
Proposed Method
Problem Transformation
原理就是给定一个权重向量 \(\omega=(1,1,...,1)\) 使得 \(\omega \cdot x=x\)
将优化\(x\)转变为优化\(\omega\)。
更进一步的:降维。
将原始决策变量分成\(γ\)组,每一组\(l\)个变量。使得 \(γ\cdot l=n\) n是决策变量个数。
如何优化ω
- 通过取一个固定的解\(x'\),我们可以将原来的优化问题Z重新表述为一个新的问题\(Z_{x'}\)。该问题使用\(x'\)作为输入参数来优化向量\(\omega\).
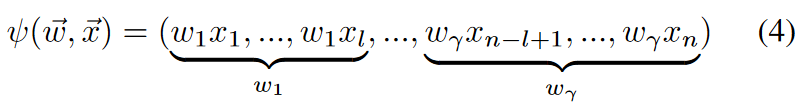
此降维方法的缺点:
原始决策变量值不能再彼此独立地改变。这在很大程度上限制了原始搜索空间中的可达解。
Ω的可搜索子空间,可以通过优化\(Z_{x'}\)来达到,主要由三个选项定义:
- \(x'\) 的选择
- 分组分案的选择(哪几个决策变量应该放在一组)
- 转移函数$ \psi(.)$ 的选择。
x'的作用
以二维决策变量为例
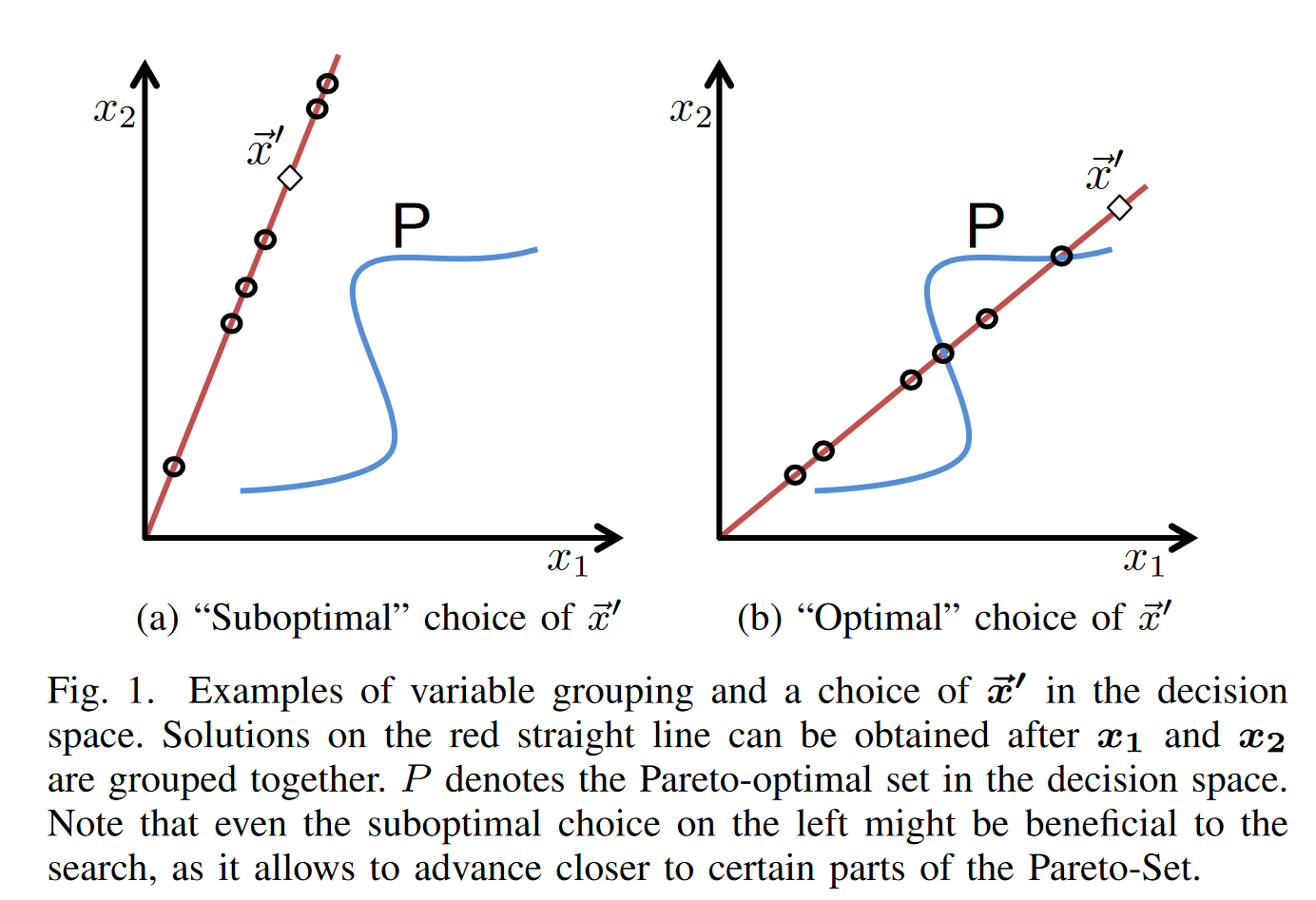
将优化空间限制在一维空间(即图中红色的线),可知可能有些最优解不能达到。但是作者认为能够接近也是很不错的。
由此可知可搜索子空间受到:
- 分组机制
- 转换函数\(\psi(.)\)
的影响。
不同分组机制的影响
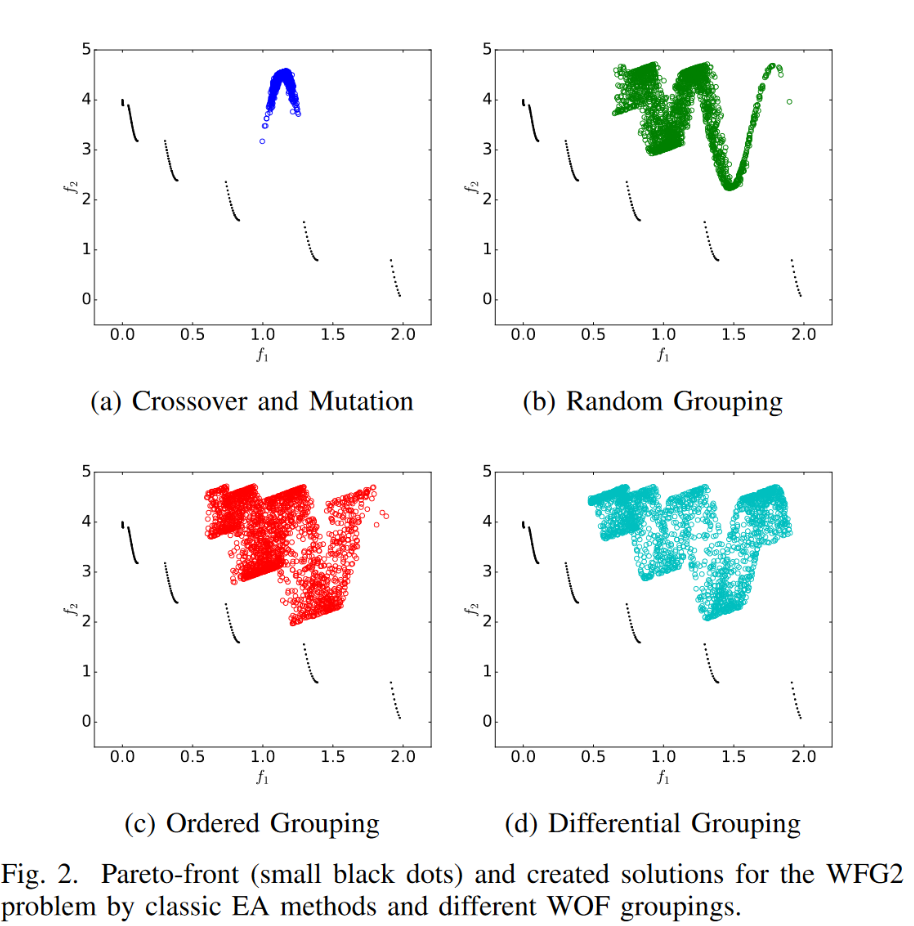
a). 普通的交叉编译
b). 随机分组然后使用\(x' \psi(.)\) 去生成子代
c). 有序分组
d). 差分分组
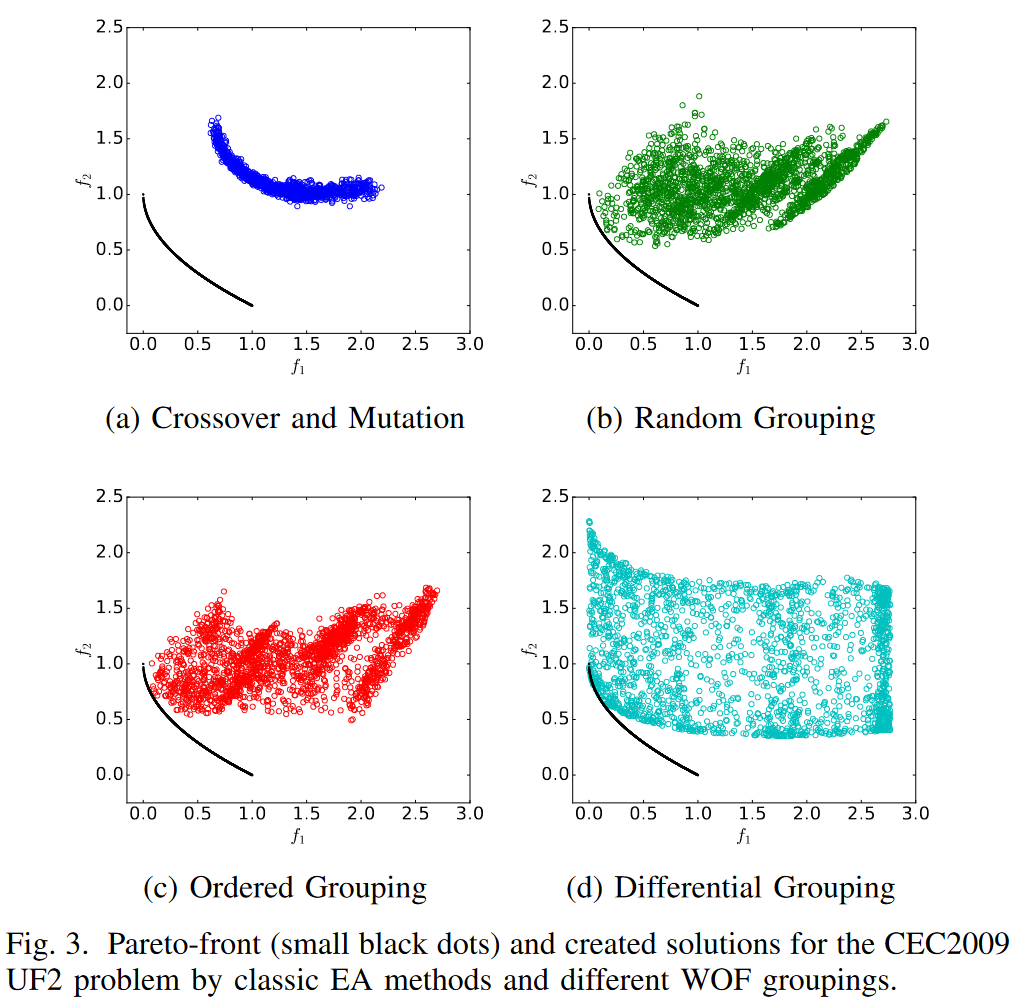
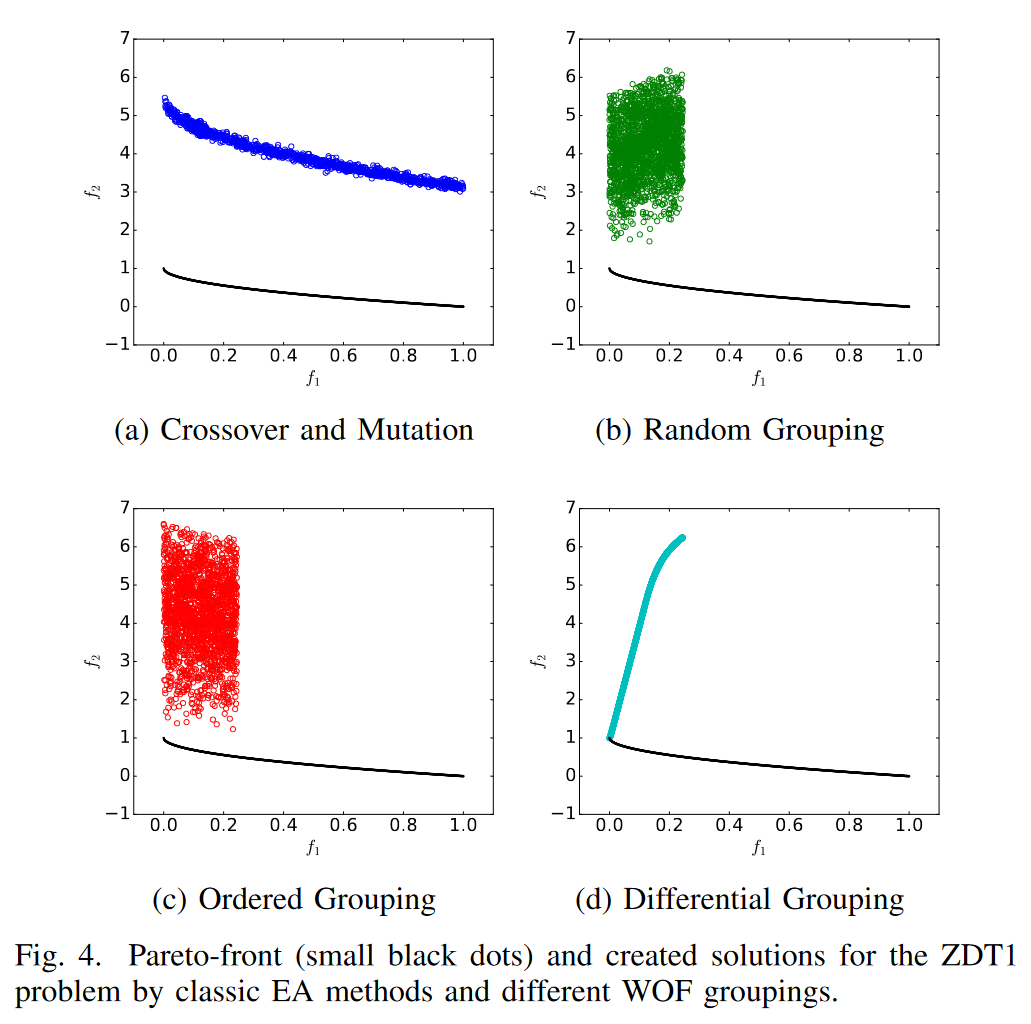
图4的表现体现了WOF方法在某些问题的局限性。
The Weighted Optimization Framework
算法流程
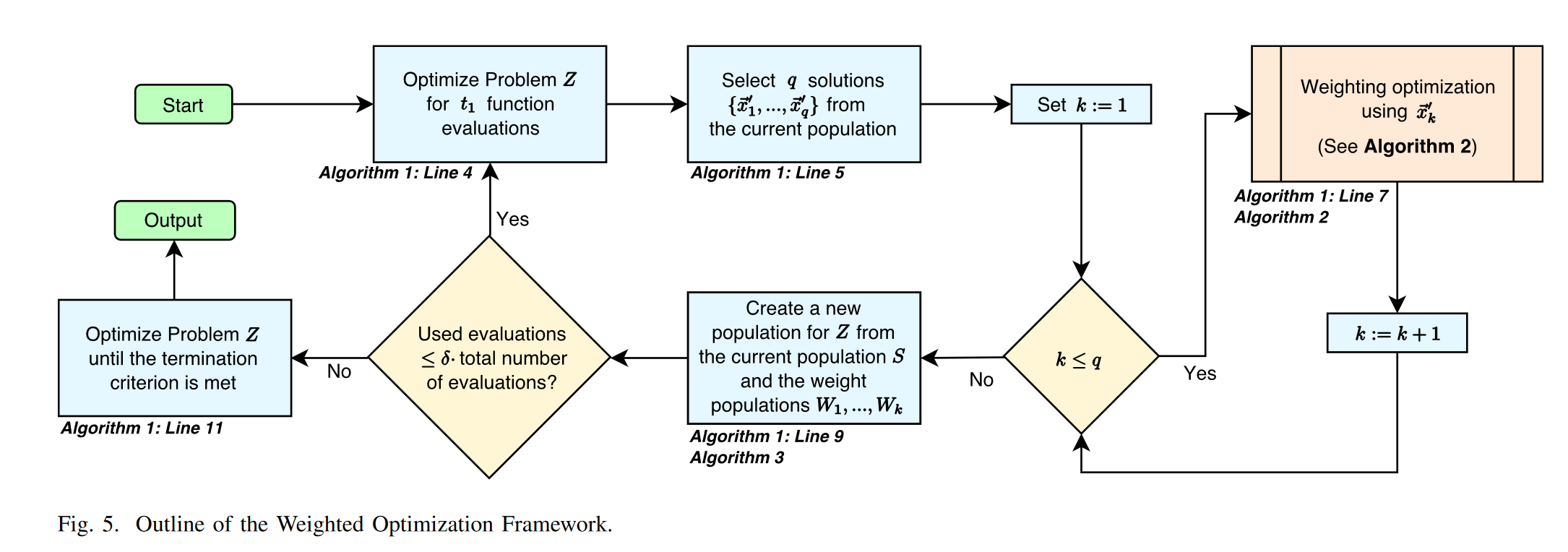
- \(t_1\)在原问题评价次数
- WOF无法在初始化的决策变量上直接开始优化
Algorithm 1:算法主体框架

以二维为例下详细解释 line5的Crowding Distance:
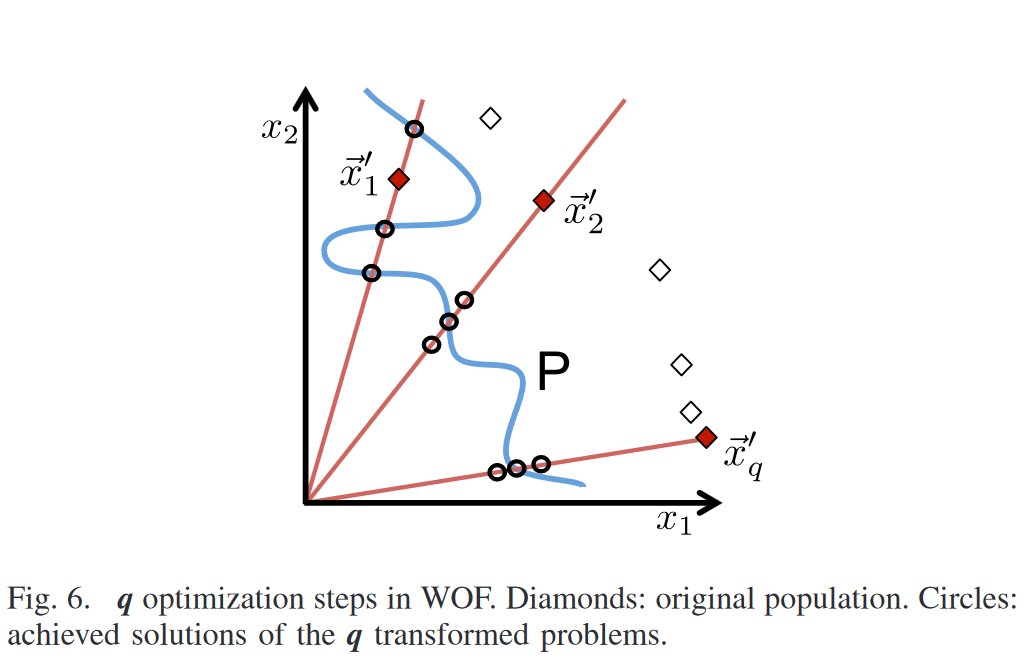
- WOF中的Q优化步骤。菱形:原始人口。圆:q变换问题的已实现解。
- 在经过A优化算法之后的种群中第一个前沿层选择q个拥挤度距离最大的个体充当 \(x'_k\)
Algorithm 2:权重优化流程
分组机制讨论
- random grouping:随机分组形成固定数量γ的大小相等的组,并将每个变量随机分配到这些组中的每个。
- Linear Grouping: 线性分组将所有n个变量按照自然顺序分配给固定的组数γ。这意味着,优化问题的第一个( n / γ )变量被分配到第一组,依此类推。这与( 4 )中的情形相对应。
- Ordered Grouping: 线性分组将所有n个变量按照自然顺序分配给固定的组数γ。这意味着,优化问题的第一个( n / γ )变量被分配到第一组,依此类推。这与( 4 )中的情形相对应。
- Differential Grouping: DG由Omidvar等人于2014年开发[23].并用于CC的单目标优化。它旨在在问题优化之前检测变量相互作用。组的数量及其大小由DG算法自动设置。简言之,DG比较在另一个变量xh改变之前和之后响应于变量xi的改变的目标函数的改变量。DG回答了以下问题:当改变xi的值时,无论另一个变量xh的值如何,\(f(x)\)的变化量是否保持不变?如果这是真的,那么变量\(x_i\)和\(x_h\)乎不会相互作用,因此它们可以被分成不同的组。除此之外,它们似乎是相互作用的,所以它们被分配到同一组。在这里使用这种方法时必须提到两个缺点。
- 如[23]中所分析的,DG算法在计算上可能会变得昂贵。假设问题包含一个数γ=(n/l)个大小相等的组,每个组有l个变量,所消耗的函数求值数为\(O(n^2/l)\)。这意味着对于使用n=2000个决策变量的完全可分离问题,DG需要n2=4 000 000个函数评估来执行分组。鉴于我们在第六节中的实验仅对整个优化过程使用了100000个函数评估,这几乎不可行。
- 如前所述,DG算法是针对单目标问题开发的。它的设计没有考虑到多个目标函数,因此不直接适用于MOP。为了使其适用于多目标优化,本文只考虑DG算法中的一个目标函数(第一个)。在未来的工作中,可能会研究使用第一个目标函数以外的函数时的含义和可能的不同结果。

Algorithm 3:合并

Transformation Functions
- ψ1—Product Transformation:
![img]()
- ψ2—p-Value Transformation:
![img]()
- ψ3—Interval-Intersection Transformation:
![img]()



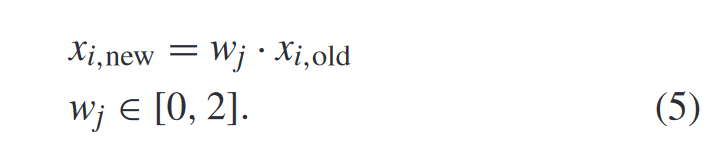
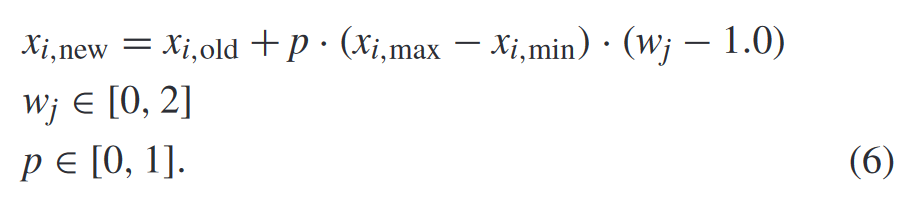
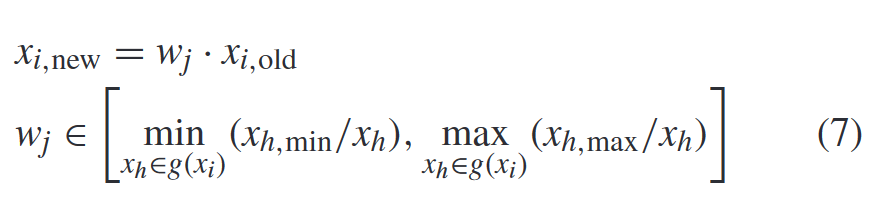

 浙公网安备 33010602011771号
浙公网安备 33010602011771号