最大子序列和问题

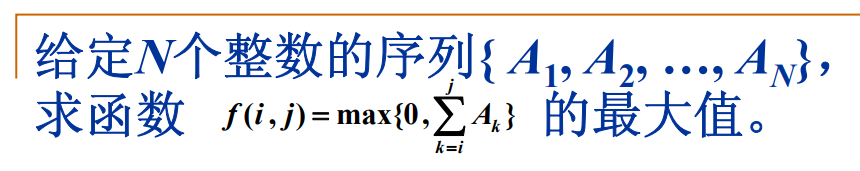
 代码：

#include <iostream>
using namespace std;

//暴力求解  T(N)=O(n^3) 
int  MaxSubSequm1(int list[], int n)
{
	int MaxSum = 0;
	for(int i = 0; i < n; i++)
	{
		for(int j = i; j < n; j++)
		{
			int ThisSum = 0;
			for(int k = i; k < j; k++)
			{
				ThisSum += list[k];
			}
			if(ThisSum > MaxSum)
			{
				MaxSum = ThisSum;
			}
		}
	}
	return MaxSum;
}

//暴力求解  T(N)=O(n^2) 
int  MaxSubSequm2(int list[], int n)
{
	int MaxSum = 0;
	for(int i = 0; i < n; i++)
	{
		int ThisSum = 0;
		for(int j = i; j < n; j++)
		{
			ThisSum += list[j];
			if(ThisSum > MaxSum)
			{
				MaxSum = ThisSum;
			}
		}
	}
	return MaxSum;
}

//分而治之 T(N)=O(nlogn) 
int Maxfun( int A, int B, int C )
{ 
    return (A > B) ? ((A > C) ? A : C) : ((B > C) ? B : C);
}
int DivideAndConquer(int list[], int left, int right)
{
	int MaxLeftSum, MaxRightSum; /* 存放左右子问题的解 */
    int MaxLeftBorderSum, MaxRightBorderSum; /*存放跨分界线的结果*/
 
    int LeftBorderSum, RightBorderSum;
    int center, i;
    
    if(left == right)
    {
    	if(list[left] < 0)
    	{
    		return 0;
		}
		else{
			return list[left];
		}
	}
	else{
		center = (left + right) / 2; 
	}
	
	MaxLeftSum = DivideAndConquer(list, left, center);
	MaxRightSum = DivideAndConquer(list, center+1, right);
	
	// 求跨分界线的最大子列和
	LeftBorderSum = 0; MaxLeftBorderSum = 0;
	RightBorderSum = 0; MaxRightBorderSum = 0;
	//从中线向左扫描
	for(int i = center; i > left; i--)
	{
		LeftBorderSum += list[i];
		if(LeftBorderSum > MaxLeftBorderSum)
		{
			MaxLeftBorderSum = LeftBorderSum;
		}
	}
	//从中线向右扫描
	for(int i = center; i < right; i++)
	{
		RightBorderSum += list[i];
		if(LeftBorderSum > MaxRightBorderSum)
		{
			MaxRightBorderSum = LeftBorderSum;
		}
	}
	
	//返回"治"的结果
	return Maxfun( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}
int MaxSubSequm3(int list[], int n)
{
	return DivideAndConquer(list, 0, n-1);
}


//在线处理 T(N)=O(n) 
int  MaxSubSequm4(int list[], int n)
{
	int ThisSum = 0;
	int MaxSum = 0;
	for(int i = 0; i < n; i++)
	{
		ThisSum += list[i]; 
		if(ThisSum > MaxSum)
		{
			MaxSum = ThisSum;
		}
		else if(ThisSum < 0)
		{
			ThisSum = 0;
		}
	}
	return MaxSum;
}  

void test()
{
	//int list[6] = { -2, 11, -4, 13, -5, -2 };
	int list[1] = {-1};
	//int list[9] = {-2,1,-3,4,-1,2,1,-5,4};
	int n;
	n = sizeof(list) / sizeof(list[0]);
	int Maxsum1, Maxsum2, Maxsum3, Maxsum4;
	Maxsum1 = MaxSubSequm1(list, n);
	
	Maxsum2 = MaxSubSequm2(list, n);
	
	Maxsum3 = MaxSubSequm3(list, n);
	
	Maxsum4 = MaxSubSequm4(list, n);
	
	cout << Maxsum1 << endl;
	cout << Maxsum2 << endl;
	cout << Maxsum2 << endl;
	cout << Maxsum4 << endl;
}

int main()
{
	test();
	
	system("pause");
	return 0;
}