网络流
网络流
网络最大流
网路最大流与网络最小割的关系及概念
什么是最大流
让一张网络从源点向汇点能流到的最大网络。
什么是最小割
使得一张网络从源点到汇点不连通的最小代价。
最大流与最小割的关系
最大流使每条增广路能够通过最大流量的和,要使图不连通,每条增广路必定要被破坏,破坏它肯定是从当条增广路的最小代价处下手,而这就恰好是此条增广路的最小限流,也就是此条增广路的网络最大流。所以网络最大流就是网络最小割。
注:接下来就以更常用的网络最大流来讲解。
网络最大流的概念
- 网络 \(G=(V,E)\),一个有向图,但是一般不具有反相边,可以有环。
- 源点 \(s\),网络输出的地方。
- 汇点 \(t\),网络汇集的地方
- 容量,每条边都有,代表总共能通过的网络。
- 最大流,从 \(s\) 到 \(t\) 能通过的最大流量。
- 增广路,能够为传输流量使得对汇点 \(t\) 得到流量做出贡献的路径。
- 残留图,走了一遍增广路后,剩下的图(实质上就是容量减少了)。
图解
以下图为例
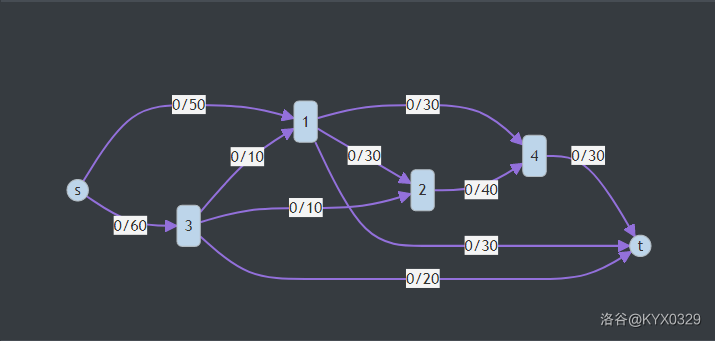
步骤:
- \(s \rightarrow 1 \rightarrow 2 \rightarrow 4 \rightarrow t\),流过的网络是 \(30\)。如下图:
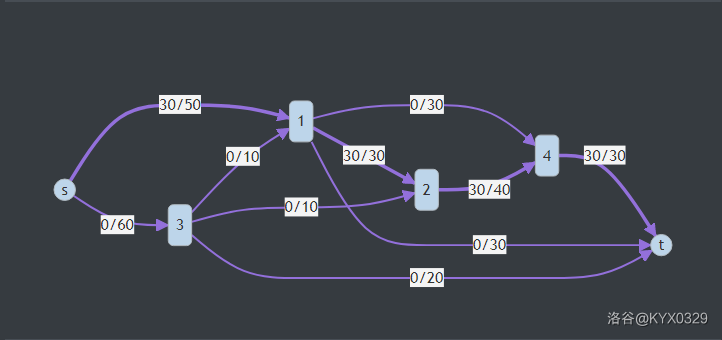
- \(s \rightarrow 1 \rightarrow t\),流过的网络是 \(20\)。如下图:
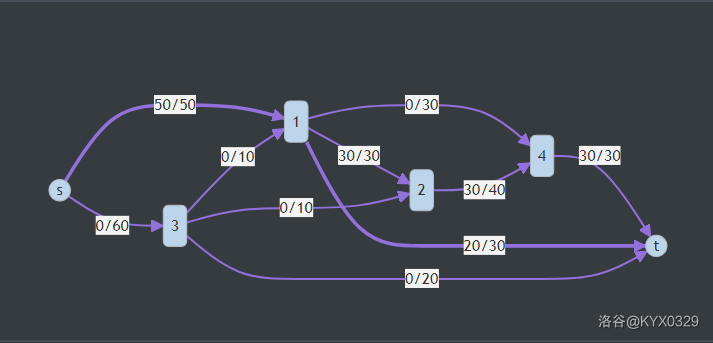
- \(s \rightarrow 3 \rightarrow 1 \rightarrow t\),流过的网络为 \(10\)。如下图:
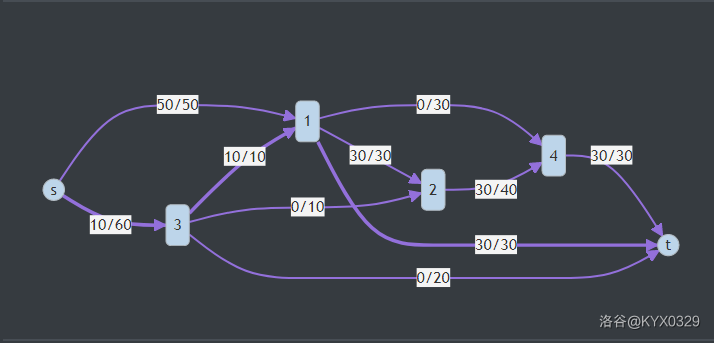
- \(s \rightarrow 3 \rightarrow t\),流过的网络为 \(20\)。如下图:
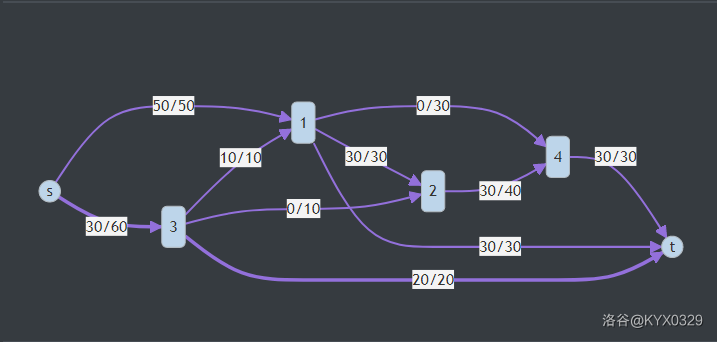
- 此时无法让更多网络流向汇点,操作结束。\(max\_flow=30+10+20+10=80\)。
如何求网络最大流(网络最小割)
EK 求网络最大流(网络最小割)
通过反复寻找源点 \(s\) 到汇点 \(t\) 之间的增广路,若有,找出增广路径上每一段的剩余容器,反之,结束循环输出答案。bfs 寻找路径在寻找增广路径时,并且更新残留图的值(本边减,反向边加)。
AC Code of Luogu P3376 【模板】网络最大流
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
const int N=1e4+10;
const int M=2e2+10;
using namespace std;
int n,m,s,t,a[M][M],pre[N],mf[N],h[N],e[N],ne[N],w[N],idx;
bool vis[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f*x;
}
void add(int x,int y,int z)
{
e[idx]=y;
ne[idx]=h[x];
w[idx]=z;
h[x]=idx++;
e[idx]=x;
ne[idx]=h[y];
w[idx]=0;
h[y]=idx++;
return;
}
bool bfs()
{
memset(vis,0,sizeof vis);
queue<int> q;
q.push(s);
vis[s]=1;
mf[s]=LONG_LONG_MAX;
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=h[x];~i;i=ne[i])
{
int to=e[i];
if(!vis[to]&&w[i])
{
vis[to]=1;
mf[to]=min(mf[x],w[i]);//能够通过的
pre[to]=i;//记录前驱
q.push(to);//加入队列
if(to==t) return 1;//能到汇点
}
}
}
return 0;
}
int EK()
{
int ans=0;//记录答案
while(bfs())//反复找增广路
{
int x=t;
while(x!=s)
{
int id=pre[x];//x的前驱
w[id]-=mf[t];//容量减少
w[id^1]+=mf[t];//流量增多
x=e[id^1];//下一个点即为
}
ans+=mf[t];
}
return ans;
}
signed main()
{
memset(h,-1,sizeof h);
n=read();
m=read();
s=read();//源点
t=read();//汇点
rep1(i,1,m)
{
int u=read();
int v=read();
int w=read();
add(u,v,w);//合并
}
cout<<EK()<<endl;//输出!!!
return 0;
}
Dinic 求网络最大流(网络最小割)
时间复杂度 \(O(n^2m)\)
前言:EK 的升级版 & 最常用的网络流算法。
本质是通过每次 bfs 分层后进行 dfs 多次增广已达到更快的速度。
算法的核心部分就是只要仍能从源点到达汇点,就进行 dfs 多次增广。为的、防止出错,在 bfs 时进行分层,每次都只能走向比当前层数大 \(1\) 的节点。
AC Code of Luogu P3376 【模板】网络最大流
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
const int N=1e4+10;
const int inf=0x3f3f3f3f3f3f3f3f;
using namespace std;
int n,m,s,t,h[N],e[N],ne[N],w[N],idx,dist[N],now[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f*x;
}
void add(int x,int y,int z)
{
e[idx]=y;
ne[idx]=h[x];
w[idx]=z;
h[x]=idx++;
e[idx]=x;
ne[idx]=h[y];
w[idx]=0;
h[y]=idx++;
return;
}
bool bfs()
{
memset(dist,inf,sizeof dist);
queue<int> q;
q.push(s);
dist[s]=0;
now[s]=h[s];
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=h[x];~i;i=ne[i])
{
int to=e[i];
if(w[i]/*还能走*/&&dist[to]==inf/*没到过*/)
{
q.push(to);
now[to]=h[to];//当前弧优化
dist[to]=dist[x]+1;//分层
if(to==t) return 1;//能到达
}
}
}
return 0;
}
int dfs(int x,int sum)
{
if(x==t) return sum;
int res=0;
for(int i=now[x];~i;i=ne[i])
{
int to=e[i];
now[x]=i;
if(w[i]/*还能通过*/&&dist[to]==dist[x]+1/*下一层*/)
{
int flow=dfs(to/*走这个点*/,min(sum,w[i])/*能通过的*/);//dfs增广
if(!flow) dist[to]=inf;//剪枝
w[i]-=flow;//正向边容量减少
w[i^1]+=flow;//反向边加上
res+=flow;//贡献
sum-=flow;//剩的
}
if(!sum) break;
}
return res;//返回此次增广贡献
}
int Dinic()//Dinic
{
int max_flow=0;
while(bfs()) max_flow+=dfs(s,inf/*因为流量守恒,所以无影响*/);//只要还能到达汇点就继续增广
return max_flow;//返回最大流
}
signed main()
{
memset(h,-1,sizeof h);
n=read();
m=read();
s=read();
t=read();
rep1(i,1,m)
{
int u=read();
int v=read();
int w=read();
add(u,v,w);//合并
}
cout<<Dinic()<<endl;//输出!!!
return 0;
}
ISAP 求网络最大流
前言:Dinic 的升级版。
先用一遍 bfs 从 \(t\) 开始分层,同时记录数组表示当前层数为 \(i\) 的点的数量,然后寻找增广路。
寻找增广路的过程中,一旦有一个点接受到的流量不能全部流出,那么就将这个点的层数提高 \(1\),如果在提高完之后出现了断层(有一层没有点了),结束算法。
AC Code of Luogu P3376 【模板】网络最大流
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
const int N=1e5+10;
const int inf=0x3f3f3f3f;
using namespace std;
int n,m,s,t,e[N],ne[N],h[N],w[N],idx,dep[N],gap[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f*x;
}
void add(int x,int y,int z)
{
e[idx]=y;
ne[idx]=h[x];
w[idx]=z;
h[x]=idx++;
e[idx]=x;
ne[idx]=h[y];
w[idx]=0;
h[y]=idx++;
return;
}
void bfs()
{
memset(dep,-1,sizeof dep);
memset(gap,0,sizeof gap);
dep[t]=0;
gap[0]=1;
queue<int> q;
q.push(t);
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=h[x];~i;i=ne[i])
{
int to=e[i];
if(~dep[to]) continue;
q.push(to);
dep[to]=dep[x]+1;
++gap[dep[to]];//记录
}
}
return;
}
int dfs(int x,int sum)
{
//以下与Dinic几乎一致
if(x==t) return sum;
int res=0;
for(int i=h[x];~i;i=ne[i])
{
int to=e[i];
if(w[i]&&dep[to]+1==dep[x])
{
int flow=dfs(to,min(w[i],sum-res));
if(flow)
{
w[i]-=flow;
w[i^1]+=flow;
res+=flow;
}
if(res==sum) return res;
}
}
//在Dinic的基础上gap优化
--gap[dep[x]];
if(!gap[dep[x]]) dep[s]=n+1;
++dep[x];
++gap[dep[x]];
return res;
}
int ISAP()
{
int maxflow=0;
bfs();
while(dep[s]<n) maxflow+=dfs(s,inf);
return maxflow;
}//ISAP,和Dinic差不多
signed main()
{
memset(h,-1,sizeof h);
n=read();
m=read();
s=read();
t=read();
rep1(i,1,m)
{
int u=read();
int v=read();
int w=read();
add(u,v,w);//建边
}
cout<<ISAP()<<endl;//输出
return 0;
}
HLPP 求网络最大流
先简单说说 HLPP 这个神仙般的算法,时间复杂度达到了惊人的 \(O(n^2\sqrt m)\)。
HLPP 预流推进算法,我们将网络理解成纵横交织的河道,源点是水库,汇点是运输目标,其余的节点就是转折区,有向边是河流。
那么它是如何实现的呢?我们允许网络在非汇点、源点的节点停留(也就是说这是一个一步一步实现的过程,并非像 Dinic 那样一口气从源点走到汇点,而是一种整体最优观念),那么对于每一个节点会拥有一个超额流(也称余流),我们用 \(ef_i\) 表示,那么我们的每个节点都要想办法将自己的超额流(如果你不是汇点那你肯定不需要留着,推送出去一定不劣),推送出去,这样才能使得我们的网络能够进入汇点 \(t\)。所以 \(t\) 最后剩下的超额流(我们会用高度 \(highh_t\) 来迫使汇点成为最低的点从而无法推送超额流),就是 \(s\) 到 \(t\) 的网络最大流(所有能够推送的已经推送了,不可能能够再推送超额流到 \(t\) 了)。
需要注意的是,为了推送不陷入死循环,我们引入每个节点的高度 \(highh_i\)。“水往低处流”,所以我们只允许从高处的节点将超额流推送给较低的点(高度的初始值由从 \(t\) 开始 bfs,被遍历到的次序决定)。高度是会改变的,如果一个节点因为高度低了而无法推送超额流那么我们就考虑提高他的高度,这个过程我们称为 重贴标签。
既然引入了 \(heighh\),那就可以说说预流推进的本质了,预留推进实际上是在不断的改变 \(heighh\) 的值,让所有的流量从源点出发,最终汇到源点(有些可能到不了汇点,让它回到源点)或汇点,最终汇点流量最大。
记住一句话,走到死路不要紧,只要每次走的都是最优的路。
还有一点想要提一下,反向连接的边可以起到反悔的作用(让流量流回去)。
接下来,我将重点讲一讲预流推进的具体实现。
定义一个优先队列,以高度为优先,因为我们的推送过程是需要从高到低的(这样才能保证你在处理当前节点的时候不会还有别的节点可以给你推送超额流)。原本每个节点高度为 \(0\),但是 \(s\) 的高度为 \(n\),这样能保证源点能够将自己的余流推送给所有与他相接的节点。然后将所有的节点的余流设为 \(0\),但是 \(s\) 的无穷大(不用担心多出来流量,走不到 \(t\) 的节点我们可以通过将高度设为 \(n+1\) 从而直接流回源点)。
考虑如何处理优先队列中的节点,我们开始处理优先队列中的队首 \(x\),对他进行推送,那么如果推送结束后,当前节点还有超额流,那么我们就重贴标签,让当前节点的高度比他能到的所有节点的最低节点高 \(1\)(原因前文有提到),保证下次一定能够推送又不至于导致有节点未能被推送(因为有 \(highh_x+1=highh_{to}\) 一限制条件)。然后再次加入优先队列,等待下一次推送(这一系列的操作都是建立在还有余流的基础下的),因为已在队列中的节点不要重复入队,所以要使用一个 \(vis\) 标记数组。
然后说一下如何推送,遍历 \(x\) 的所有出边,若发现 \(highh_x+1=highh_{to}\),那么这条边就可以进行推送(因为原定的顺序是 \(bfs\) 制定的所以说一开始的所有与 \(x\) 相邻的节点都会满足这个条件,而修改高度之后就不一定了,所以要求重贴标签必须将需进行重贴的节点的高度恰好比它所能够到达的高度最低的节点大 \(1\)),每次的推送量显然不能超过允许通过的流量也不能多于当前节点超额流,所以有推送流量 \(d=\min(ef_x,w_i)\),只要出现了流量的转移就必须要重新入队(如果已经在队列里就不用了),值得注意的就是反向边的允许通过流量一定要加上 \(d\),不然就没法回头了。
补充一点,重贴标记如果失败就让他到源点上面去,由于重贴失败了,所以它一定能够流回源点。
最终 \(ef_t\) 就是网络最大流。
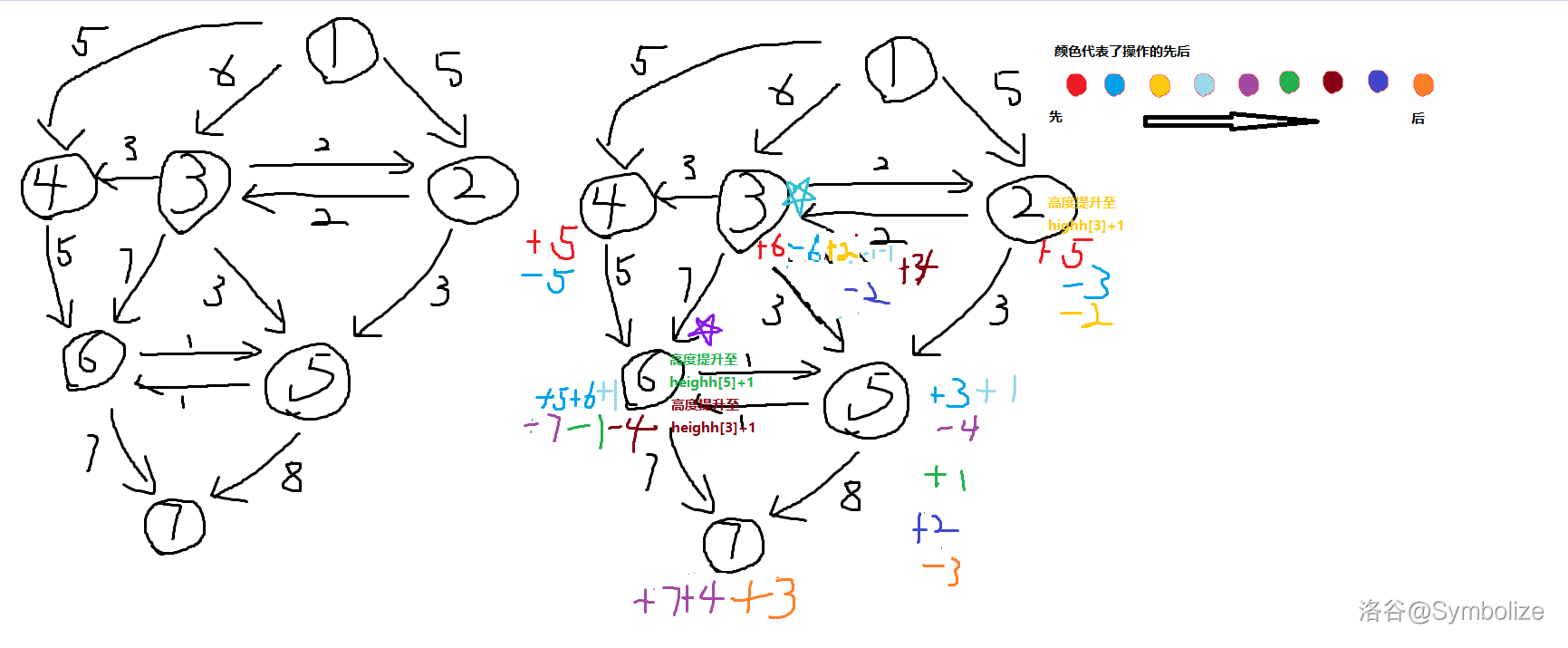
花了很长时间才将 luogu 样例的维护过程画了出来,但还是很丑,希望大家见谅,感性理解一下吧,特别是上面文字没完全明白的同学,重点注意薄荷绿五角星位置的流量出入与深紫色五角星节点的高度改变,搞清楚这个图那么这个算法就没什么太大问题。
优化:
可以使用 ISAP 的 \(gap\) 数组进行优化,这里就简单一提了。
非源点高度设为 \(0\) 会增加很多运行次数,把高度设为到 \(t\) 的距离明显能少跑很多。bfs 反向遍历一遍就可以了。
然后就是我们的 \(gap\) 数组优化了!我们发现如果一个节点,他它没有别的节点高,就一定无法使得流量到达 \(t\)。那把它提到 \(s\) 上端不就好了?它将直接流向 \(s\),不会浪费操作次数,那如何判断呢?用 \(gap\) 存储每个高度的个数就可以了!
AC Code of Luogu P4722 【模板】最大流 加强版 / 预流推进
/*
Luogu name: Symbolize
Luogu uid: 672793
*/
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(register int i=l;i<=r;++i)
#define rep2(i,l,r) for(register int i=l;i>=r;--i)
#define rep3(i,x,y,z) for(register int i=x[y];~i;i=z[i])
#define rep4(i,x) for(auto i:x)
#define debug() puts("----------")
const int N=1e6+10;
const int inf=0x3f3f3f3f3f3f3f3f;
using namespace std;
int n,m,s,t,e[N],h[N],ne[N],w[N],idx,highh[N],ef[N],gap[N],vis[N];
struct cmp{bool operator()(int a,int b)const{return highh[a]<highh[b];}};//手动定义排序规则
priority_queue<int,vector<int>,cmp> q;
int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return x*f;
}
void add(int x,int y,int z)
{
idx+=2;//建立双向边
e[idx]=y;
ne[idx]=h[x];
w[idx]=z;
h[x]=idx;
e[idx+1]=x;
ne[idx+1]=h[y];
w[idx+1]=0;//反相边的权值为0
h[y]=idx+1;
return;
}
bool bfs()//bfs把初始的高度定义为到t的距离,s则为n
{
queue<int> q;
memset(highh,0x3f,sizeof highh);
highh[t]=0;//t的高度为0,起点
q.push(t);//从t开始
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=h[x];~i;i=ne[i])
{
int to=e[i];
if(w[i^1]/*剩余容量不为0*/&&highh[to]>highh[x]+1/*可以流向当前目标节点*/)
{
highh[to]=highh[x]+1;//更新高度
q.push(to);//进队
}
}
}
//判断是否连通
if(highh[s]!=inf) return 1;
return 0;
}
void push(int x)
{
rep3(i,h,x,ne)
{
int to=e[i];
if(w[i]/*剩余容量不为0*/&&highh[to]+1==highh[x]/*高度满足*/&&highh[to]<inf)
{
int d=min(ef[x],w[i]);//推送余留不得大于当前节点余流和剩余容量
w[i]-=d;//当前边的容量减掉
w[i^1]+=d;//方向边的流量加上
ef[x]-=d;//当前节点余留减少
ef[to]+=d;//增加目标余流
if(to!=s/*不为源点*/&&to!=t/*不为汇点*/&&!vis[to]/*不在优先队列中*/)
{
q.push(to);//加入优先队列等待推送
vis[to]=1;//以加入优先队列
}
if(!ef[x]) break;//没有余流了
}
}
return;
}
void relabel(int x)//重贴标签
{
highh[x]=inf;
rep3(i,h,x,ne)
{
int to=e[i];
if(w[i]/*剩余容量不为0*/&&highh[to]+1<highh[x]/*保证下一次可以推送即可,不要过高*/) highh[x]=highh[to]+1;
}
return;
}
int HLPP()//核心操作
{
if(!bfs()) return 0;
highh[s]=n;//源点的高度为n
memset(gap,0,sizeof gap);
rep1(i,1,n) if(highh[i]<inf/*没法到达的点就不用了*/) ++gap[highh[i]];//gap优化
//为了防止发生一些问题,单独跑一边源点
rep3(i,h,s,ne)
{
int to=e[i];
int dist=w[i];
if(dist&&highh[to]<inf)
{
w[i]-=dist;//当前边容量减少
w[i^1]+=dist;//反相边流量增加
ef[s]-=dist;//当前节点余流推送
ef[to]+=dist;//被推送节点余流增加
if(to!=s/*不为源点*/&&to!=t/*不为汇点*/&&!vis[to]/*不在优先队列中*/)
{
q.push(to);//等待推送
vis[to]=1;//已进入优先队列
}
}
}
while(!q.empty())
{
int x=q.top();//当前推送节点
vis[x]=0;//取消标记
q.pop();//出队
push(x);//推送
if(ef[x])//还有余流
{
if(!--gap[highh[x]]/*如果本高度只有它一个*/) rep1(j,1,n) if(j!=s/*不为源点*/&&j!=t/*不为汇点*/&&highh[j]>highh[x]/*不可能被推送到汇点*/&&highh[j]<n+1/*高度不等于n+1*/) highh[j]=n+1;//把不可能到达汇点的所有点高度调为n+1,直接流向源点
relabel(x);//重贴标签,保证下次能够推送
++gap[highh[x]];//新的高度
q.push(x);//因为还有余流所以进队
vis[x]=1;//标记
}
}
return ef[t];//返回汇点的余流,这就是网络最大流
}
signed main()
{
memset(h,-1,sizeof h);
n=read();
m=read();
s=read();
t=read();
rep1(i,1,m)
{
int u=read();
int v=read();
int w=read();
add(u,v,w);//连边
}
cout<<HLPP()<<endl;
return 0;
}
网络最小费用最大流
网络最小费用最大流概念
前言
全名最小费用最大流。
网络最大费用最大流就是把最短路改为最长路。
概念
在保证网络最大流的前提下花费最少费用。通过分层的方式使得比 EK 跑更少时间的 bfs。
MCMF 问题(Min Cost Max Flow)
你可以理解成用 SPFA 求增广路。
简单来说就是用 SPFA 求增广路,这样就可以在找增广路的同时满足费用最小。
以 EK 为例:
这里只解释易错点(其他的基本和 EK 求网络最大流一样)。
存图:同样建立双向边,但是正向边的限流为给定值,反向边的限流为 \(0\);正向边的费用为给定值,反向边的费用为给定值的相反数。
求增广路:正常跑 SPFA 只不过要记录前驱与此增广路路可以通过的最大流。因为有多次调用,所以记得清空数组和队列!
和求网络最大流唯一的不同是要记录费用,总费用 \(=\) 此条增广路的最大流 \(\times\) 经过路径的单位费用和。
AC Code of Luogu P3381 【模板】最小费用最大流
/*
Luogu name: Symbolize
Luogu uid: 672793
*/
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(register int i=l;i<=r;++i)
#define rep2(i,l,r) for(register int i=l;i>=r;--i)
#define rep3(i,x,y,z) for(register int i=x[y];~i;i=z[i])
#define rep4(i,x) for(auto i:x)
#define debug() puts("----------")
const int N=1e5+10;
const int inf=0x3f3f3f3f3f3f3f3f;
using namespace std;
int n,m,s,t,h[N],e[N],ne[N],w[N],c[N],idx,dist[N],now[N],max_flow,min_cost;
bool vis[N];
int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f*x;
}
void add(int x,int y,int z,int cost)
{
e[idx]=y;
ne[idx]=h[x];
w[idx]=z;
c[idx]=cost;
h[x]=idx++;
e[idx]=x;
ne[idx]=h[y];
w[idx]=0;
c[idx]=-cost;
h[y]=idx++;
return;
}
bool spfa()
{
queue<int> q;
memset(dist,inf,sizeof dist);
memcpy(now,h,sizeof h);
q.push(s);
dist[s]=0;
vis[s]=1;
while(!q.empty())
{
int x=q.front();
q.pop();
vis[x]=0;
rep3(i,h,x,ne)
{
int to=e[i];
if(w[i]&&dist[to]>dist[x]+c[i])
{
dist[to]=dist[x]+c[i];
if(!vis[to])
{
q.push(to);
vis[to]=1;
}
}
}
}
if(dist[t]!=inf) return 1;
return 0;
}
int dfs(int x,int sum)
{
if(x==t) return sum;
vis[x]=1;
int res=0;
for(int i=now[x];~i;i=ne[i])
{
int to=e[i];
now[x]=i;
if(!vis[to]&&w[i]&&dist[to]==dist[x]+c[i])
{
int flow=dfs(to,min(sum,w[i]));
if(flow)
{
w[i]-=flow;
w[i^1]+=flow;
res+=flow;
sum-=flow;
min_cost+=flow*c[i];
}
if(!sum) break;
}
}
vis[x]=0;
return res;
}
void MCMF()
{
while(spfa())
{
int x=dfs(s,inf);
while(x)
{
max_flow+=x;
x=dfs(s,inf);
}
}
return;
}
signed main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
memset(h,-1,sizeof h);
n=read();
m=read();
s=read();
t=read();
rep1(i,1,m)
{
int u=read();
int v=read();
int w=read();
int c=read();
add(u,v,w,c);
}
MCMF();
cout<<max_flow<<' '<<min_cost<<endl;
return 0;
}
有上下界的网络流
无源汇网络上下界可行流
整体上的思路是把上下界拆分掉。
我们考虑是否存在满足流量平衡的情况下满足上下界限制。
流量平衡:每个点都满足流入它的流量等于流出它的流量。
我们可以将每条边的上界减掉下界得到一个新的图,这个图是可以跑网络最大流的。
但这样流量就不平衡了,怎么办呢?突破口在源点与汇点,这两个点是不需要保证流量平衡的,虽然标题叫“无源汇网络上下界可行流”,但是我们可以建造虚拟的超级源汇点。
我们计算 \(in_x\) 为 \(x\) 节点的入流和,\(out_x\) 为 \(x\) 节点的出流和。因为流量平衡,所以 \(x\) 的流量一定是 \(\min(in_x,out_x)\)。若 \(in_x \neq out_x\),则此时流量不平衡。所以,我们需要对所有的 \(in_x > out_x\),连一条从 \(s\) 到 \(x\) 容量为 \(in_x-out_x\) 的边来补齐由于流量平衡而带来的流量损失;反之,我们需要对所有的 \(in_x < out_x\),连一条从 \(x\) 到 \(t\) 容量为 \(out_x-in_x\) 的边来补齐由于流量平衡而带来的流量损失;而对于 \(in_x=out_x\),不需要建边。
简单来说,就是用源点的汇点去让每一个 \(x\) 节点平衡所损失的流量。
最后的步骤总结:
- 统计出 \(in_x\) 与 \(out_x\)。
- 用上界减下界,得到新的图。
- 建立虚拟源汇点,向其余节点连边,使得网络图除源汇点外流量平衡。
- 跑网络最大流,若满流,则存在可行流。
AC Code of LibreOJ 115 无源汇有上下界可行流
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
const int N=1e5+10;
const int inf=0x3f3f3f3f3f3f3f3f;
using namespace std;
int n,m,s,t,h[N],e[N],ne[N],w[N],idx,dist[N],now[N],low[N],limits[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f*x;
}
void add(int x,int y,int z)
{
e[idx]=y;
ne[idx]=h[x];
w[idx]=z;
h[x]=idx++;
e[idx]=x;
ne[idx]=h[y];
w[idx]=0;
h[y]=idx++;
return;
}
bool bfs()
{
memset(dist,inf,sizeof dist);
queue<int> q;
q.push(s);
dist[s]=0;
now[s]=h[s];
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=h[x];~i;i=ne[i])
{
int to=e[i];
if(w[i]&&dist[to]==inf)
{
q.push(to);
now[to]=h[to];
dist[to]=dist[x]+1;
if(to==t) return 1;
}
}
}
return 0;
}
int dfs(int x,int sum)
{
if(x==t) return sum;
int res=0;
for(int i=now[x];~i;i=ne[i])
{
int to=e[i];
now[x]=i;
if(w[i]&&dist[to]==dist[x]+1)
{
int flow=dfs(to,min(sum,w[i]));
if(!flow) dist[to]=inf;
w[i]-=flow;
w[i^1]+=flow;
res+=flow;
sum-=flow;
}
}
return res;
}
int Dinic()
{
int max_flow=0;
while(bfs()) max_flow+=dfs(s,inf);
return max_flow;
}//Dinic模板
signed main()
{
memset(h,-1,sizeof h);
n=read();
m=read();
s=n+1;
t=n+2;
rep1(i,0,m-1)
{
int u=read();
int v=read();
int lower=read();
int upper=read();
add(u,v,upper-lower);
limits[u]+=lower;//加上出边下界(limits存的是出边下界和减入边下界和)
limits[v]-=lower;//减去入边下界(limits存的是出边下界和减入边下界和)
low[i]=lower;//因为要分离下界,所以最后还要加上
}
int flow=0;
rep1(i,1,n)
{
if(limits[i]>0)//正的,让超级汇点消化
{
flow+=limits[i];//预估流量
add(i,t,limits[i]);
}
if(limits[i]<0) add(s,i,-limits[i]);//负的,让源点消化
}
if(flow==Dinic())//满足
{
puts("YES");
rep1(i,0,m-1) cout<<w[i<<1|1]+low[i]<<endl;
}
else puts("NO");//不满足
return 0;
}
有源汇网络上下界可行流
就是在无源汇的上下界网络可行流中加了两个点,这两个点不需要流量守恒而已。
那显然 \(s\) 流出的流量和 \(t\) 流入的流量是相同的,所以只需要多建一条从 \(t\) 到 \(s\) 容量为无限大的边就行了。
有源汇网络上下界最大流
就是在可行的基础上求最大。
我们可以先找一个可行流 \(flow\)。此时虚拟的源汇点的边显然是没有了,继续跑可行流是无意义的。
但要注意,此时的可行流并不代表就是最大流。因为原图中的很多边是无法被跑满的。
但我们可以发现,原图中还有能跑的,那我们就在跑完可行流后再在原图上跑一遍最大流,在拿原图的最大流与 \(flow\) 相加不就可以了吗?
所以总结下步骤:
- 跑上下界可行流,得到 \(flow\)。
- 删去原图源汇点之间的边(防止死循环)。
- 若存在可行流,输出 \(flow\) 与最大流的和。
AC Code of LibreOJ 116 有源汇有上下界最大流
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
const int N=1e5+10;
const int inf=0x3f3f3f3f3f3f3f3f;
using namespace std;
int n,m,S,T,s,t,h[N],e[N],ne[N],w[N],idx,dist[N],now[N],low[N],limits[N],t_h[N]/*用来保存原图*/;
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f*x;
}
void add(int x,int y,int z)
{
e[idx]=y;
ne[idx]=h[x];
w[idx]=z;
h[x]=idx++;
e[idx]=x;
ne[idx]=h[y];
w[idx]=0;
h[y]=idx++;
return;
}
bool bfs(int s,int t)
{
memset(dist,inf,sizeof dist);
queue<int> q;
q.push(s);
dist[s]=0;
now[s]=h[s];
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=h[x];~i;i=ne[i])
{
int to=e[i];
if(w[i]&&dist[to]==inf)
{
q.push(to);
now[to]=h[to];
dist[to]=dist[x]+1;
if(to==t) return 1;
}
}
}
return 0;
}
int dfs(int x,int sum,int s,int t)
{
if(x==t) return sum;
int res=0;
for(int i=now[x];~i;i=ne[i])
{
int to=e[i];
now[x]=i;
if(w[i]&&dist[to]==dist[x]+1)
{
int flow=dfs(to,min(sum,w[i]),s,t);
if(!flow) dist[to]=inf;
w[i]-=flow;
w[i^1]+=flow;
res+=flow;
sum-=flow;
}
}
return res;
}
int Dinic(int s,int t)
{
int max_flow=0;
while(bfs(s,t)) max_flow+=dfs(s,inf,s,t);
return max_flow;
}//Dinic模板
signed main()
{
memset(h,-1,sizeof h);
n=read();
m=read();
S=read();
T=read();
s=n+1;
t=n+2;
rep1(i,0,m-1)
{
int u=read();
int v=read();
int lower=read();
int upper=read();
add(u,v,upper-lower);
limits[u]+=lower;//加上出边下界(limits存的是出边下界和减入边下界和)
limits[v]-=lower;//减去入边下界(limits存的是出边下界和减入边下界和)
low[i]=lower;//因为要分离下界,所以最后还要加上
}
memcpy(t_h,h,sizeof h);//把原图复制下来
int flow=0;
rep1(i,1,n)
{
if(limits[i]>0)//正的,让超级汇点消化
{
flow+=limits[i];//预估流量
add(i,t,limits[i]);
}
if(limits[i]<0) add(s,i,-limits[i]);//负的,让源点消化
}
add(T,S,inf);
if(flow==Dinic(s,t))//满足
{
memcpy(h,t_h,sizeof t_h);
cout<<w[idx-1]+Dinic(S,T)<<endl;
}
else puts("please go home to sleep");
return 0;
}
有源汇网络上下界最小流
我们可以在建 \(t \rightarrow s\) 这条边之前跑一遍可行流,连上 \(t \rightarrow s\) 后跑最大流,这次最大流的流量就是最小的,两者相加即可。
AC Code of LibreOJ 117 有源汇有上下界最小流
#include<bits/stdc++.h>
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
const int N=1e6+10;
const int inf=0x3f3f3f3f;
using namespace std;
int n,m,S,T,s,t,h[N],e[N],ne[N],w[N],idx,dep[N],now[N],low[N],limits[N],gap[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f*x;
}
void add(int x,int y,int z)
{
e[idx]=y;
ne[idx]=h[x];
w[idx]=z;
h[x]=idx++;
e[idx]=x;
ne[idx]=h[y];
w[idx]=0;
h[y]=idx++;
return;
}
void bfs(int s,int t)
{
memset(dep,-1,sizeof dep);
memset(gap,0,sizeof gap);
dep[t]=0;
gap[0]=1;
queue<int> q;
q.push(t);
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=h[x];~i;i=ne[i])
{
int to=e[i];
if(~dep[to]) continue;
q.push(to);
dep[to]=dep[x]+1;
++gap[dep[to]];
}
}
return;
}
int dfs(int x,int sum,int s,int t)
{
if(x==t) return sum;
int res=0;
for(int i=h[x];~i;i=ne[i])
{
int to=e[i];
if(w[i]&&dep[to]+1==dep[x])
{
int flow=dfs(to,min(w[i],sum-res),s,t);
if(flow)
{
w[i]-=flow;
w[i^1]+=flow;
res+=flow;
}
if(res==sum) return res;
}
}
--gap[dep[x]];
if(!gap[dep[x]]) dep[s]=n+1;
++dep[x];
++gap[dep[x]];
return res;
}
int ISAP(int s,int t)
{
int maxflow=0;
bfs(s,t);
while(dep[s]<n) maxflow+=dfs(s,inf,s,t);
return maxflow;
}//ISAP模板
signed main()
{
memset(h,-1,sizeof h);
n=read();
m=read();
S=read();
T=read();
s=n+1;
t=n+2;
rep1(i,0,m-1)
{
int u=read();
int v=read();
int lower=read();
int upper=read();
add(u,v,upper-lower);
limits[u]+=lower;//加上出边下界(limits存的是出边下界和减入边下界和)
limits[v]-=lower;//减去入边下界(limits存的是出边下界和减入边下界和)
low[i]=lower;//因为要分离下界,所以最后还要加上
}
int flow=0;
rep1(i,1,n)
{
if(limits[i]>0)//正的,让超级汇点消化
{
flow+=limits[i];//预估流量
add(i,t,limits[i]);
}
if(limits[i]<0) add(s,i,-limits[i]);//负的,让源点消化
}
int ans=ISAP(s,t);
add(T,S,inf);
ans+=ISAP(s,t);
if(flow==ans) cout<<w[idx-1]<<endl;
else puts("please go home to sleep");
return 0;
}
最小割树
就是多次询问最小割的问题。
将图转化为树,将 \(u\) 到 \(v\) 的最小割转化到树上。
Dinic 的最后一次 bfs 就是在求一个最小割。所以任意选 \(s\) 和 \(t\) 进行网络最小割(网络最大流)操作,在 \(s\) 与 \(t\) 中连一条边。通过分治补全树。
因为树只要少一条边就不连通,所以联系最小割的性质,我们就会发现 \(u\) 到 \(v\) 的最小割为 \(u\) 到 \(v\) 中的所有路径的最小值。
由此就能推出所有的答案。
AC Code of Luogu P4897 【模板】最小割树(Gomory-Hu Tree)
#include<bits/stdc++.h>
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
const int N=5e2+10;
const int M=6e3+10;
const int inf=0x3f3f3f3f;
using namespace std;
int q,n,m,s,t,h[N],e[M],ne[M],w[M],idx,now[N],dist[N],tr[N],ans[N][N],s1[N],s2[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f*x;
}
void add(int x,int y,int z)
{
e[idx]=y;
ne[idx]=h[x];
w[idx]=z;
h[x]=idx++;
e[idx]=x;
ne[idx]=h[y];
w[idx]=0;
h[y]=idx++;
return;
}
bool bfs()
{
memset(dist,0,sizeof dist);
queue<int> q;
q.push(s);
now[s]=h[s];
dist[s]=1;
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=h[x];~i;i=ne[i])
{
int to=e[i];
if(!dist[to]&&w[i])
{
dist[to]=dist[x]+1;
now[to]=h[to];
if(to==t) return 1;
q.push(to);
}
}
}
return 0;
}
int dfs(int x,int sum)
{
if(x==t) return sum;
int res=0;
for(int i=now[x];~i&&res<sum;i=ne[i])
{
int to=e[i];
now[x]=i;
if (dist[to]==dist[x]+1&&w[i])
{
int flow=dfs(to,min(w[i],sum-res));
if(!flow) dist[to]=-1;
w[i]-=flow;
w[i^1]+=flow;
res+=flow;
}
}
return res;
}
void init()
{
for(int i=0;i<idx;i+=2) w[i]+=w[i^1],w[i^1]=0;
return;
}//退流
int Dinic()
{
int max_flow=0;
while(bfs()) max_flow+=dfs(s,inf);
init();
return max_flow;
}//Dinic模板
void build(int l,int r)
{
if(l==r) return;
s=tr[l];
t=tr[l+1];
int x=Dinic(),S=tr[l],T=tr[l+1];//记得记录上次的源点与汇点
ans[s][t]=ans[t][s]=x;//更新值
int len1=0,len2=0;
rep1(i,l,r)
{
if(dist[tr[i]]) s1[++len1]=tr[i];
else s2[++len2]=tr[i];
}
rep1(i,1,len1) tr[i+l-1]=s1[i];
rep1(i,1,len2) tr[len1+l+i-1]=s2[i];
//分治
build(l,l+len1-1);
build(l+len1,r);
//预处理答案
rep1(i,1,len1)
{
rep1(j,1,len2)
{
int I=tr[i+l-1],J=tr[len1+j+l-1];
ans[I][J]=ans[J][I]=min(min(ans[I][S],ans[S][T]),ans[T][J]);
}
}
return;
}
signed main()
{
memset(h,-1,sizeof h);
memset(ans,inf,sizeof ans);
n=read();
m=read();
rep1(i,1,m)
{
int u=read();
int v=read();
int w=read();
add(u,v,w);//建双向边
add(v,u,w);//建双向边
}
rep1(i,0,n) tr[i]=i;
build(0,n);
q=read();
while(q--) cout<<ans[read()][read()]<<endl;//Q次询问,需要预处理答案
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号