快速傅里叶变换(FFT)
前言
本算法分为 计算机离散傅里叶变换(DFT) 与 快速傅里叶变换(FFT) 两大部分,以及 快速傅里叶逆变换(IFFT)的补充。
正文
DFT 与 FFT 定义
DFT(计算机离散傅里叶变换)
计算机离散傅里叶变换(DFT),是傅里叶变换在时域和频域上都呈现离散的形式,将时域信号的采样变换为在离散时间傅里叶变换(DTFT)频域的采样。在形式上,变换两端(时域和频域上)的序列是有限长的,而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT,也应当将其看作经过周期延拓成为周期信号再作变换。在实际应用中通常采用快速傅里叶变换以高效计算DFT。——百度百科
简单来说就是通过计算 \(\omega_n^k\) 实现多项式的系数表示法与点值表示法的快速转换。
FFT(快速傅里叶变换)
快速傅里叶变换(Fast Fourier Transform),即利用计算机计算离散傅里叶变换(DFT)的高效、快速计算方法的统称,简称 FFT。快速傅里叶变换是 1965 年由 J.W.库利 和 T.W.图基 提出的。
单位根
如果复数 \(\omega\) 满足 \(\omega^n=1\) 则称 \(\omega\) 为 \(n\) 次单位根。
如何寻找单位根呢?
我们先引入单位圆。
单位圆,即以原点为圆心,半径为 \(1\) 的圆。
我们将这个圆 \(n\) 等分,取这 \(n\) 个等分点按逆时针编号,我们就得到 \(\omega\) 了。
举个例子,当 \(n=8\) 时:
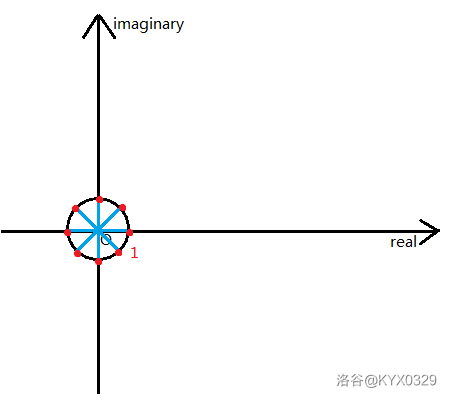
我们定义幅角最小的那个的向量被称为 \(n\) 次单位根,写作 \(\omega_n^1\),其中定有实数解 \(1\)。
单位根的意义是 \(x^n=1\) 的解,一定会有 \(n\) 个。
为什么这 \(n\) 个根会均匀分布在单位圆上?因为单位圆上的点模长都为 \(1\),幂运算又可以理解为一个单位圆上向量的 \(n\) 次方即幅角的 \(n\) 倍,所以就是在找 \(\theta\) 角的度数,使得 \(n \times \theta=k \times 360^{\circ}\)。
通过三角函数可得:\(\omega_n^k=\cos \frac{k}{n}2\pi+i\sin \frac{k}{n}2\pi\)。
单位根还有以下三个性质:
- \(\omega_n^k=\omega_{2n}^{2k}\);
- \(\omega_n^k=-\omega_n^{k+\frac{n}{2}}\);
- \(\omega_n^0=\omega_n^n=1\)。
DFT
对于函数 \(f(x)=y=a_0x^0+a^1x_1+\dots+a_nx^n\),规定点值表示中的 \(n\) 个 \(x\) 为 \(n\) 个模长为 \(1\) 的单位根,得到一种特殊的点值表示法,这种点值就叫 DFT。
FFT
实现
DFT 的时间复杂度仍然是 \(O(n^2)\) 的,所以需要利用单位根的性质加速运算。
对于多项式
可以将其分为两部分
显然有
以上就是蝴蝶变换。
由此,因为在解决 \(A_0(\omega_{\frac{n}{2}}^k)\) 与 \(A_1(\omega_{\frac{n}{2}}^k)\) 时,我们已经知道 \(A_0(\omega_n^k)\) 与 \(A_1(\omega_n^{k+\frac{n}{2}})\)。
所以可以使用分治进行 FFT。
优化
我们来模拟一下,分治的过程,如下图:
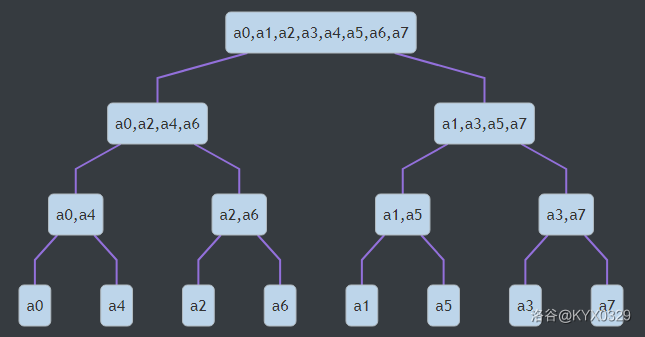
不难发现,在二进制下,最终序列与原序列在二进制是翻转的关系,如下:
原序列十进制: 0 1 2 3 4 5 6 7
原序列二进制: 000 001 010 011 100 101 110 111
最终序列十进制: 0 4 2 6 1 5 3 7
最终序列二进制:000 100 010 110 001 101 011 111
所以我们可以预处理最终状态,进行合并操作。
IFFT
FFT 之后,为了转回系数表达法还需要 IFFT,把多项式 \(A(x)\) 的结果作为 \(B(x)\) 的系数,再将单位根的倒数代入 \(B(x)\)。
证明:
FFT 解决乘法高精度
AC Code of Luogu 【模板】A*B Problem 升级版(FFT 快速傅里叶变换)
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
const int N=1e7+10;
const double pi=acos(-1);//圆周率
using namespace std;
typedef complex<double> cd;//复数类的定义
int rev[N],ans[N];//存储二进制反转结果
cd a[N],b[N];//存储中间转换结果
char s1[N],s2[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f*x;
}
void FFT(cd *f,int n,int key)
{
rep1(i,0,n-1) if(i<rev[i]) swap(f[i],f[rev[i]]);//预处理最终序列
//模拟合并过程
for(int i=1;i<n;i<<=1)//模拟合并的次数
{
cd wn=exp(cd(0,key*pi/i));//计算单位复根
for(int j=0;j<n;j+=(i<<1))//模拟合并一次的组数
{
cd wnk(1,0);//每个独立序列都是从0开始的
rep1(k,j,i+j-1)//模拟合并的每一组
{
//蝴蝶变换
cd x=f[k],y=wnk*f[k+i];
f[k]=x+y;
f[k+i]=x-y;
wnk*=wn;//计算下一次复根
}
}
}
///IFFT的情况
if(key==-1) rep1(i,0,n-1) f[i]/=n;
return;
}
signed main()
{
cin>>s1>>s2;
int l1=strlen(s1)-1;
int l2=strlen(s2)-1;
rep1(i,0,l1) a[i]=(double)(s1[l1-i]-'0');
rep1(i,0,l2) b[i]=(double)(s2[l2-i]-'0');
int x=0,s=1;//bit表示数组的二进制位数,s表示分割的长度
while((1<<x)<=l1+l2+2) s<<=1,++x;//找到一个2的整数次幂可以容纳这两个串的乘积
rep1(i,0,(1<<x)-1) rev[i]=(rev[i>>1]>>1)|((i&1)<<(x-1));//二进制反转
//FFT
FFT(a,s,1);
FFT(b,s,1);
rep1(i,0,s-1) a[i]*=b[i];//点值相乘
//IFFT
FFT(a,s,-1);
//存入输出数组
rep1(i,0,s-1)
{
ans[i]+=(int)(a[i].real()+0.5);
ans[i+1]+=ans[i]/10;//进位
ans[i]%=10;//此位
}
int i=l1+l2+2;
while(~i&&!ans[i]) --i;//去掉前导0
if(i==-1) puts("0");//相乘为0
while(~i) cout<<ans[i--];//因为高位在后,低位在前 所以逆序输出
putchar('\n');
return 0;
}
FFT 解决多项式乘法
AC Code of Luogu P3803 【模板】多项式乘法(FFT)
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
#define debug() puts("----------")
const int N=1e7+10;
const int inf=0x3f3f3f3f3f3f3f3f;
const double pi=acos(-1);
using namespace std;
typedef complex<int> ci;
typedef complex<double> cd;
char s1[N],s2[N];
cd a[N],b[N];
int n,m,rev[N],ans[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f*x;
}
void FFT(cd *f,int n,int key)
{
rep1(i,0,n-1) if(i<rev[i]) swap(f[i],f[rev[i]]);
for(int i=1;i<n;i<<=1)
{
cd wn=exp(cd(0,key*pi/i));
for(int j=0;j<n;j+=(i<<1))
{
cd wnk(1,0);
rep1(k,j,i+j-1)
{
cd x=f[k],y=wnk*f[k+i];
f[k]=x+y;
f[k+i]=x-y;
wnk*=wn;
}
}
}
if(key==-1) rep1(i,0,n) a[i]/=n;
return;
}//FFT & IFFT 板子
signed main()
{
// #ifndef ONLINE_JUDGE
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
// #endif
n=read();
m=read();
rep1(i,0,n) a[i]=(double)read();
rep1(i,0,m) b[i]=(double)read();
int x=0,s=1;
while(s<=n+m) s<<=1,++x;
rep1(i,0,s-1) rev[i]=(rev[i>>1]>>1)|((i&1)<<(x-1));
FFT(a,s,1);
FFT(b,s,1);
rep1(i,0,s) a[i]*=b[i];
FFT(a,s,-1);
rep1(i,0,n+m) cout<<(int)(a[i].real()+0.5)<<' ';
putchar('\n');
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号