AC 自动机

AC 自动机

原理

KMP + Trie树
这是一种多模式串的匹配算法。

相较于 KMP 算法在运行多模式串的匹配时只需一次遍历即可,而 KMP 要针对不同的子序列对母序列进行多次遍历。

讲解

第一步

构造 Trie 树。

insert 函数代码

void insert(int x)
{
	int p=0;
	for(int i=0;s[x][i];i++)
	{
		int u=s[x][i]-'a';
		if(!tr[p][u]) tr[p][u]=++idx;
		p=tr[p][u];
	}
	mp[x]=p;
}

---

第二步

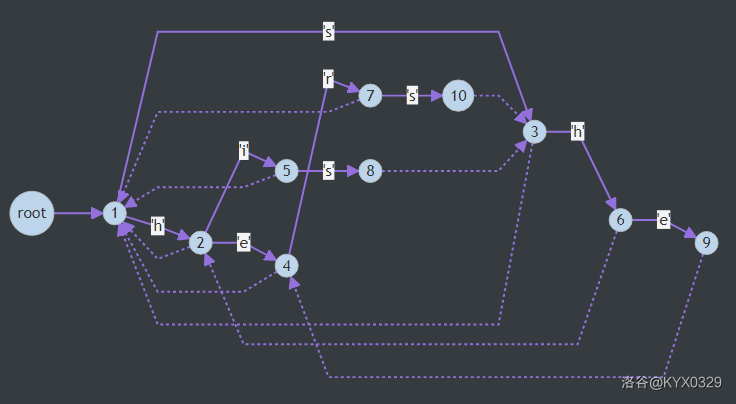
构造 fail 指针。使当前字符失配时跳转到具有最长公共前后缀的字符继续匹配。如同 KMP，AC 自动机在匹配时如果当前字符匹配失败，那么利用 fail 指针进行跳转。由此可知如果跳转，跳转后的串的前缀，必为跳转前的模式串的后缀并且跳转的新位置的深度（匹配字符个数）一定小于跳之前的节点。所以我们可以利用 bfs 在 Trie 树上面进行每一层节点 fail 指针的求解。

以集合 \(\mathbf{S}=\){he,his,hers,she}$ 为例：

build 函数代码

void build()
{
	int hh=0,tt=-1;
	rep1(i,0,25)
	{
		if(tr[0][i])
		{
			ne[tr[0][i]]=0;
			q[++tt]=tr[0][i];
		}
	}
	while(tt>=hh)
	{
		int t=q[hh++];
		rep1(i,0,25)
		{
			if(tr[t][i])
			{
				ne[tr[t][i]]=tr[ne[t]][i];
				q[++tt]=tr[t][i];
			}
			else tr[t][i]=tr[ne[t]][i];
		}
	}
}

---

完整代码

AC Code of Luogu P5357 【模板】AC 自动机（二次加强版）

#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
const int N=1e6+10;
using namespace std;
using namespace std;
int n,idx,tr[N][30],ne[N],cnt[N],mp[N],q[N]; 
string s[N],a;
inline int read()
{
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=(x<<1)+(x<<3)+(ch^48);
		ch=getchar();
	}
	return f*x;
}
void insert(int x)
{
	int p=0;
	for(int i=0;s[x][i];i++)
	{
		int u=s[x][i]-'a';
		if(!tr[p][u]) tr[p][u]=++idx;
		p=tr[p][u];
	}
	mp[x]=p;
}
void build()
{
	int hh=0,tt=-1;
	rep1(i,0,25)
	{
		if(tr[0][i])
		{
			ne[tr[0][i]]=0;
			q[++tt]=tr[0][i];
		}
	}
	while(tt>=hh)
	{
		int t=q[hh++];
		rep1(i,0,25)
		{
			if(tr[t][i])
			{
				ne[tr[t][i]]=tr[ne[t]][i];
				q[++tt]=tr[t][i];
			}
			else tr[t][i]=tr[ne[t]][i];
		}
	}
}
void doit()
{
	cin>>a;
	int j=0;
	for(int i=0;a[i];i++)
	{
		int u=a[i]-'a';
		j=tr[j][u];
		++cnt[j];
	}
}
signed main()
{
	n=read();
	rep1(i,1,n)
	{
		cin>>s[i];
		insert(i);
	}
	build();
	doit();
	rep2(i,idx,0) cnt[ne[q[i]]]+=cnt[q[i]];
	rep1(i,1,n) cout<<cnt[mp[i]]<<endl;
	return 0;
}