线段树
普通线段树
简介
线段树是一种时间复杂度为 \(O(log_N)\) 的维护区间信息的高级数据结构。
主要功能有:
- 区间修改
- 区间查询
下面是区间 \([1,9]\) 的线段树(未加点权)
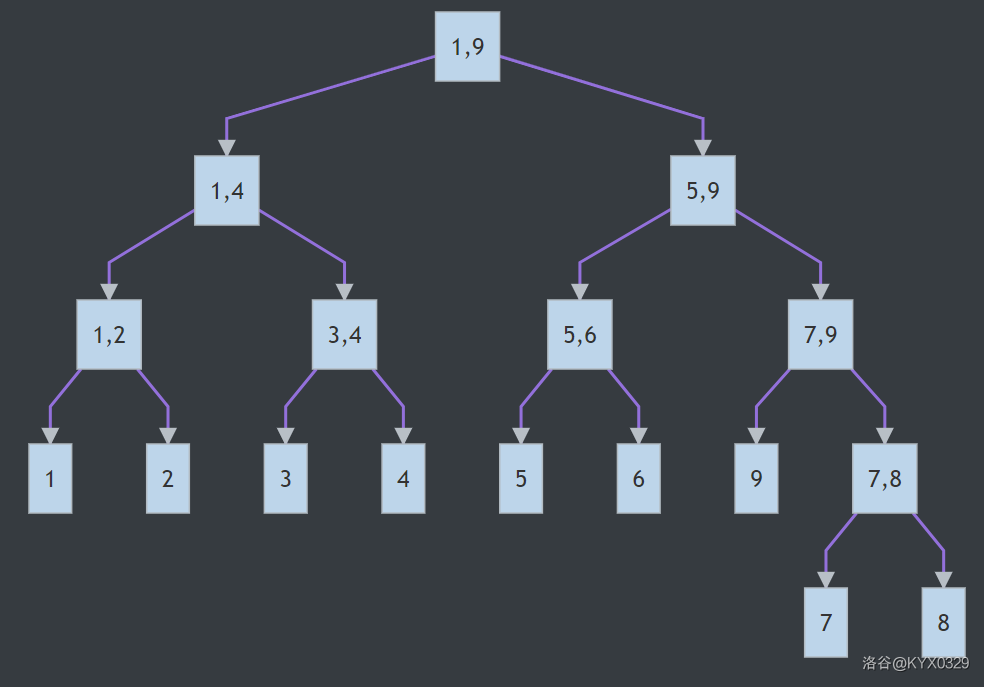
主要操作是使用 build 建树,将叶子结点的信息通过 push_up 向上维护到更大的区间,加入了 lazytag 快速区间修改,再用 push_down 向下维护小区间,最后使用 query 进行查询。
下面以Luogu P3372 【模板】线段树 1为例题讲解
build
此函数用于建图,从更节点开始建图,最开始范围为 \([1,n]\),建图使用二分分治,每次分别递归维护左子树与右子树,知道遍历到叶子结点,把已知值附到叶子节点上,向上维护每个节点。
build 函数代码
void build(int p,int l,int r)//递归建树
{
tag[p]=0;//懒标记清空
if(l==r)//叶子节点
{
tr[p]=a[l];//赋值
return;//结束递归
}
int mid=l+r>>1;
build(ls(p),l,mid);//二分分治左子树
build(rs(p),mid+1,r);//二分分治右子树
push_up(p);//向上维护
return;//结束递归
}
push_up
向上维护节点,也就是当前节点的值为左儿子值加右儿子值。
push_up 函数代码
void push_up(int p){tr[p]=tr[ls(p)]+tr[rs(p)];}//向上维护,当前节点的和等于左节点的和加右节点的和
push_down
向下维护,因为使用了懒标记,所以需要把标记的值传递下去,有多少节点就有多少个单位的懒标记。
push_down 函数代码
void push_down(int p,int l,int r)//向下维护
{
int mid=l+r>>1;
tag[ls(p)]+=tag[p];//左子树懒标记的传递
tag[rs(p)]+=tag[p];//右子树懒标记的传递
tr[ls(p)]+=tag[p]*(mid-l+1);//左儿子的值加上一个数,mid-l+1表示在左子树内,当前要修改的个数,与tag[p]相乘即为当前增加的值
tr[rs(p)]+=tag[p]*(r-mid);//右儿子的值加上一个数,r-mid表示在右子树内,当前要修改的个数,与tag[p]相乘即为当前增加的值
tag[p]=0;//当前节点懒标记清空
return;
}
lazytag
标记懒标记,输入的修改区间需要分配到每个节点上,如果此节点代表区间被完全覆盖,则说明此区间被选取,赋予其懒标记,在进行向下维护,最后向上维护确保正确。
lazytag 函数代码
void lazytag(int pl,int pr,int l,int r,int p,int k)//懒标记
{
if(pl<=l&&pr>=r)//被包含
{
tr[p]+=k*(r-l+1);//r-l+1为区间包含的节点个数,总的增加量即修改量乘节点个数
tag[p]+=k;//懒标记的叠加
return;
}
push_down(p,l,r);//向下维护
int mid=l+r>>1;
if(pl<=mid) lazytag(pl,pr,l,mid,ls(p),k);//在左边
if(pr>mid) lazytag(pl,pr,mid+1,r,rs(p),k);//在右边
push_up(p);//向下维护
return;
}
query
询问操作,与 lazytag 基本相同,也是将询问区间分配到每个节点上。
query 函数代码
int query(int pl,int pr,int l,int r,int p)
{
int ans=0;
if(pl<=l&&pr>=r) return tr[p];//完全被包含,直接返回此段长度
push_down(p,l,r);//向下维护
int mid=l+r>>1;
if(pl<=mid) ans+=query(pl,pr,l,mid,ls(p));//剩下的在左边
if(pr>mid) ans+=query(pl,pr,mid+1,r,rs(p));//剩下的在右边
return ans;//返回答案
}
完整代码
AC Code of P3372 【模板】线段树 1
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
const int N=1e6+10;
using namespace std;
int n,m,opt,x,y,a[N],tr[N],tag[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f*x;
}
int ls(int x){return x<<1;}//左儿子
int rs(int x){return x<<1|1;}//右儿子
void push_up(int p){tr[p]=tr[ls(p)]+tr[rs(p)];}//向上维护,当前节点的和等于左节点的和加右节点的和
void build(int p,int l,int r)//递归建树
{
tag[p]=0;//懒标记清空
if(l==r)//叶子节点
{
tr[p]=a[l];//赋值
return;//结束递归
}
int mid=l+r>>1;
build(ls(p),l,mid);//二分分治左子树
build(rs(p),mid+1,r);//二分分治右子树
push_up(p);//向上维护
return;//结束递归
}
void push_down(int p,int l,int r)//向下维护
{
int mid=l+r>>1;
tag[ls(p)]+=tag[p];//左子树懒标记的传递
tag[rs(p)]+=tag[p];//右子树懒标记的传递
tr[ls(p)]+=tag[p]*(mid-l+1);//左儿子的值加上一个数,mid-l+1表示在左子树内,当前要修改的个数,与tag[p]相乘即为当前增加的值
tr[rs(p)]+=tag[p]*(r-mid);//右儿子的值加上一个数,r-mid表示在右子树内,当前要修改的个数,与tag[p]相乘即为当前增加的值
tag[p]=0;//当前节点懒标记清空
return;
}
void lazytag(int pl,int pr,int l,int r,int p,int k)//懒标记
{
if(pl<=l&&pr>=r)//被包含
{
tr[p]+=k*(r-l+1);//r-l+1为区间包含的节点个数,总的增加量即修改量乘节点个数
tag[p]+=k;//懒标记的叠加
return;
}
push_down(p,l,r);//向下维护
int mid=l+r>>1;
if(pl<=mid) lazytag(pl,pr,l,mid,ls(p),k);//在左边
if(pr>mid) lazytag(pl,pr,mid+1,r,rs(p),k);//在右边
push_up(p);//向下维护
return;
}
int query(int pl,int pr,int l,int r,int p)
{
int ans=0;
if(pl<=l&&pr>=r) return tr[p];//完全被包含,直接返回此段长度
push_down(p,l,r);//向下维护
int mid=l+r>>1;
if(pl<=mid) ans+=query(pl,pr,l,mid,ls(p));//剩下的在左边
if(pr>mid) ans+=query(pl,pr,mid+1,r,rs(p));//剩下的在右边
return ans;//返回答案
}
signed main()
{
n=read();
m=read();
rep1(i,1,n) a[i]=read();
build(1,1,n);//建图
while(m--)
{
opt=read();
x=read();
y=read();
if(opt==1) lazytag(x,y,1,n,1,read());//标记
else cout<<query(x,y,1,n,1)<<endl;//输出
}
return 0;
}
可持久化权值线段树
简介
给线段树增加历史点来维护历史数据,使得我们能在较短时间内查询历史数据。
完整代码
AC Code of Luogu P3834 【模板】可持久化线段树 2
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
const int N=1e5+10;
using namespace std;
int n,m,a[N],root[N],idx;
vector<int> v;
struct node
{
int l,r;
int cnt;
}tr[N*21];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f*x;
}
int build(int l,int r)
{
int p=++idx;//新状态
if(l==r) return p;//遍历到叶子结点了
int mid=l+r>>1;
tr[p]={build(l,mid),build(mid+1,r),0};//递归建树并存值
return p;
}
int insert(int p,int id,int l,int r)//插入
{
int q=++idx;//新状态
tr[q]=tr[p];//继承上一状态
if(l==r)//叶子结点
{
++tr[q].cnt;//个数加一
return q;
}
int mid=l+r>>1;
if(id<=mid) tr[q].l=insert(tr[p].l,id,l,mid);//在左子树
else tr[q].r=insert(tr[p].r,id,mid+1,r);//在右子树
tr[q].cnt=tr[tr[q].l].cnt+tr[tr[q].r].cnt;//向上维护
return q;
}
int query(int p,int q,int k,int l,int r)//询问
{
if(l==r) return r;//叶子结点
int mid=l+r>>1;
int cnt=tr[tr[q].l].cnt-tr[tr[p].l].cnt;//方便计算
if(k<=cnt) return query(tr[p].l,tr[q].l,k,l,mid);//第k小在左子树
else return query(tr[p].r,tr[q].r,k-cnt,mid+1,r);//第k小在右子树
}
signed main()
{
n=read();
m=read();
rep1(i,1,n) v.push_back(a[i]=read());
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());//离散化
root[0]=build(0,v.size()-1);//最初始状态
rep1(i,1,n) root[i]=insert(root[i-1],lower_bound(v.begin(),v.end(),a[i])-v.begin(),0,v.size()-1);//插入,得到新的状态
while(m--)
{
int l=read();
int r=read();
int k=read();
cout<<v[query(root[l-1],root[r],k,0,v.size()-1)]<<endl;//询问
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号