Trie 树

普通 Trie 树

前言

就是字典树。

概念

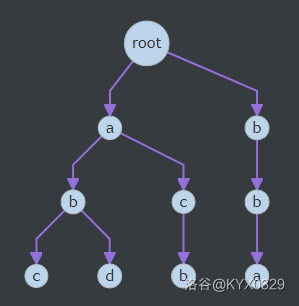
将字符串之间的公共前缀合并。

例如：
abc
abd
acb
cba

AC Code of Luogu P8306 【模板】字典树

#include<bits/stdc++.h>
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
const int N=3e6+10;
using namespace std;
int t,n,q,idx,tag[N];
map<char,int> mp;
int tr[N][65];
char s[N];
inline int read()
{
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=(x<<1)+(x<<3)+(ch^48);
		ch=getchar();
	}
	return f*x;
}
void insert()
{
	int len=strlen(s+1),p=0;
	rep1(i,1,len)
	{
		if(!tr[p][mp[s[i]]]) tr[p][mp[s[i]]]=++idx;//若没访问过，给一个标号 
		p=tr[p][mp[s[i]]]; //下个节点 
		++tag[p];//节点个数加1 
	}
	return;
}
int query()//询问 
{
	int len=strlen(s+1),p=0;
	rep1(i,1,len)
	{
		if(!tr[p][mp[s[i]]]) return 0;//若此节点无值，则答案一定为0 
		p=tr[p][mp[s[i]]]; //下个节点 
	}
	return tag[p];//结束了，输出这个节点下面的节点个数 
}
void init()//把字符转为数字 
{
	int id=0;
	for(char i='a';i<='z';i++) mp[i]=++id;
	for(char i='A';i<='Z';i++) mp[i]=++id;
	for(char i='0';i<='9';i++) mp[i]=++id;
	return;
}
void getans()
{
	n=read();
	q=read();
	rep1(i,1,n)
	{
		cin>>(s+1);
		insert();
	}
	while(q--)
	{
		cin>>s+1;
		cout<<query()<<endl;
	}
	rep1(i,0,idx)
	{
		tag[i]=0;
		rep1(j,0,65) tr[i][j]=0;
	}
	idx=0;
	return;
}
signed main()
{
	init();//预处理 
	t=read();
	while(t--) getans();//t组数据 
	return 0;
}

可持久化 Trie 树

保存多个版本，每次只修改被添加或值被修改的节点，而保留没有被改动的节点，在上一个版本的基础上连边，使最后每个版本的 Trie 树的根遍历所能分离出的 Trie 树都是完整且包含全部信息的。

例如：
cat
rat
cab
frg

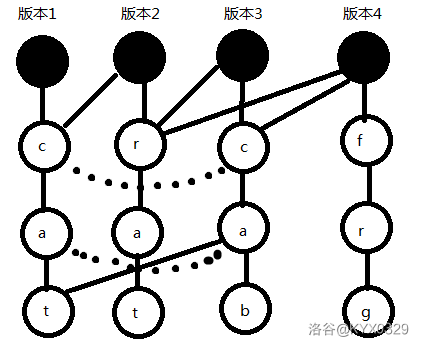
对于每一个版本，从该版本根节点出发，找到历史各个版本的信息。

AC Code of Luogu P4735 最大异或和

#include<bits/stdc++.h>
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
const int N=6e5+10;
using namespace std;
int s[N],tr[N*25][2],max_id[N*25],root[N],idx,n,m;
inline int read()
{
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=(x<<1)+(x<<3)+(ch^48);
		ch=getchar();
	}
	return f*x;
}
//递归版插入 
//void insert(int i/*第i个插入的数*/,int k/*取到第k位*/,int p/*上一个插入的数的节点号*/,int q/*当前节点号*/)
//{
//    if(k<0)
//    {
//        max_id[q]=i;//当前q为叶节点，记录当前节点所能到达的最大范围i
//        return;
//    }
//    int v=s[i]>>k&1;//取出当前要处理的数的第k位
//    if(p) tr[q][v^1]=tr[p][v^1];//如果前一个节点有当前节点没有的分支，直接复制历史信息
//    tr[q][v]=++idx;//新的序号 
//    insert(i,k-1,tr[p][v],tr[q][v]);//递归 
//    max_id[q]=max(max_id[tr[q][0]],max_id[tr[q][1]]);//回溯，保存子节点最大范围的值
//    return;
//}
void insert(int k,int p,int q)//max_id其实就是当前新加的节点在前缀异或和数组s的位置
{
    max_id[q]=k;//取出第k位 
    rep2(i,23,0)
    {
        int v=s[k]>>i&1;//取出第k位 
        if(p) tr[q][v^1]=tr[p][v^1];//如果前一个节点有当前节点没有的分支，直接复制历史信息
        tr[q][v]=++idx;//新的序号
        max_id[tr[q][v]]=k;
        q=tr[q][v];//下个点 
		p=tr[p][v];//下个点 
    }
}
int query(int p,int l,int c)//查询 
{
	//x是s[n]^x，从高位到低位逐位检索二进制每一位上能跟x异或结果最大的数
    rep2(i,23,0)
    {
        int v=c>>i&1;
        if(max_id[tr[p][v^1]]>=l) p=tr[p][v^1];//能否走最好的选择 
        else p=tr[p][v];//退而求其次
    }
    return c^s[max_id[p]];
}
signed main()
{
	//前缀异或和
    n=read();
    m=read();
    s[0]=0;
    max_id[0]=-1;
    root[0]=++idx;//最初版本 
    insert(0,0,root[0]);
    rep1(i,1,n)
    {
        int x=read();
        root[i]=++idx;
        s[i]=s[i-1]^x;
        insert(i,root[i-1],root[i]);
    }
    while(m--)
    {
        char op[2];
      	cin>>op;
        if(*op=='A')
        {
            int x=read();
            root[++n]=++idx;
            s[n]=s[n-1]^x;
            insert(n,root[n-1],root[n]);
        }
        else
        {
            int l=read();
            int r=read();
            int x=read();
    		cout<<query(root[r-1],l-1,s[n]^x)<<endl;
        }
    }
    return 0;
}