树链剖分
概念
首先要明确以下几个点:
- 重儿子:对于每一个非叶子节点,它的所有儿子中,以此儿子为根的子树的节点个数最多的儿子为重儿子。
- 轻儿子:除重儿子以外的儿子。
- 重边:重儿子与父节点连成的边。
- 重链:连续的重边组成的链。
例图:
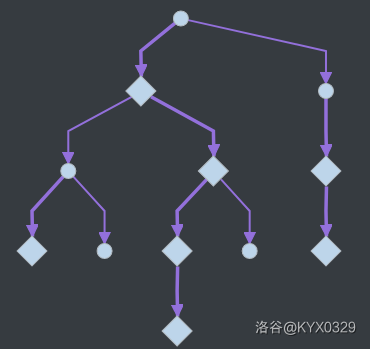
图中的菱形节点为重儿子,粗边为重边。
接着我们就能发现每个轻儿子都有一条以它为起点的重链。
处理的问题
\(x\) 到 \(y\) 的最短路径上的所有点权和
最短路径实际上就是 LCA。
我们每次让深度更大的点为 \(x\)。
用 \(ans\) 累加 \(x\) 到 \(x\) 所在重链顶端的区间点权和,把 \(x\) 跳到 \(x\) 所在链顶端的上面一个点,直到两个点处于一条链,再累加此时两个点的距离就可以了。
这个过程可以使用线段树解决。
修改 \(x\) 到 \(y\) 的最短路径上所有点的值
与上一个问题同理,也就是线段树的懒标记。
\(x\) 为根的子树的点权和
存下来每个点的子树和,直接线段树查询就可以了。
修改 \(x\) 为根的子树的所有点的值
与上一个问题相同,也就是线段树的懒标记。
预处理
我们会发现有很多东西需要预处理出来,这需要使用两个 dfs。
dfs1
处理内容:
- \(dep_i\):\(i\) 每个节点的深度。
- \(fa_i\):\(i\) 节点的父节点。
- \(lex_i\):以 \(i\) 节点为根的子树的大小。
- \(son_i\):非叶子节点 \(i\) 的重儿子。
dfs1 函数代码
void dfs1(int x,int last,int deep)
{
dep[x]=deep;//深度
fa[x]=last;//父节点
len[x]=1;//子树包含节点个数
int max_son=-1;//重儿子的子树包含节点个数
for(int i=h[x];~i;i=ne[i])
{
int to=e[i];
if(to==last) continue;//若为父节点则跳过
dfs1(to,x,deep+1);//dfs
len[x]+=len[to];//子树包含节点个数累加
if(len[to]>max_son)//若此儿子的子树包含节点个数大于了之前的重儿子
{
son[x]=to;//更新重儿子
max_son=len[to];//更新重儿子子树包含的节点个数
}
}
return;
}
dfs2
处理内容:
- \(id_i\):\(i\) 节点的新编号。
- \(top_i\):\(i\) 节点所在链的链顶。
注:先遍历重儿子,这样重链的编号是连续的方便后面的操作。
dfs2 函数代码
void dfs2(int x,int front)
{
id[x]=++cnt;//标记新的编号
W[cnt]=w[x];//给新标号原来的权值
top[x]=front;//记录链顶
if(!son[x]) return;//叶子节点
dfs2(son[x],front);//先处理重儿子
for(int i=h[x];~i;i=ne[i])
{
int to=e[i];
if(to==fa[x]||to==son[x]) continue;//前面处理过重儿子了,所以为父节点或重儿子时都跳过
dfs2(to,to);//对于每一个轻儿子都有一条自己为链头的重链
}
return;
}
完整代码
AC Code of Luogu P3384 【模板】重链剖分/树链剖分
#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define rep1(i,l,r) for(int i=l;i<=r;i++)
#define rep2(i,l,r) for(int i=l;i>=r;i--)
const int N=2e5+10;
using namespace std;
int n,m,r,mod,opt,h[N],e[N],ne[N],w[N],idx,W[N],dep[N],len[N],fa[N],son[N],top[N],id[N],cnt,tr[N],tag[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f*x;
}
void add(int x,int y)
{
e[idx]=y;
ne[idx]=h[x];
h[x]=idx++;
return;
}
void dfs1(int x,int last,int deep)
{
dep[x]=deep;//深度
fa[x]=last;//父节点
len[x]=1;//子树包含节点个数
int max_son=-1;//重儿子的子树包含节点个数
for(int i=h[x];~i;i=ne[i])
{
int to=e[i];
if(to==last) continue;//若为父节点则跳过
dfs1(to,x,deep+1);//dfs
len[x]+=len[to];//子树包含节点个数累加
if(len[to]>max_son)//若此儿子的子树包含节点个数大于了之前的重儿子
{
son[x]=to;//更新重儿子
max_son=len[to];//更新重儿子子树包含的节点个数
}
}
return;
}
void dfs2(int x,int front)
{
id[x]=++cnt;//标记新的编号
W[cnt]=w[x];//给新标号原来的权值
top[x]=front;//记录链顶
if(!son[x]) return;//叶子节点
dfs2(son[x],front);//先处理重儿子
for(int i=h[x];~i;i=ne[i])
{
int to=e[i];
if(to==fa[x]||to==son[x]) continue;//前面处理过重儿子了,所以为父节点或重儿子时都跳过
dfs2(to,to);//对于每一个轻儿子都有一条自己为链头的重链
}
return;
}
int ls(int p){return p<<1;}
int rs(int p){return p<<1|1;}
void push_up(int p){tr[p]=(tr[ls(p)]+tr[rs(p)])%mod;}
void build(int p,int l,int r)
{
tag[p]=0;
if(l==r)
{
tr[p]=W[l]%mod;
return;
}
int mid=l+r>>1;
build(ls(p),l,mid);
build(rs(p),mid+1,r);
push_up(p);
return;
}
void push_down(int p,int l,int r)
{
int mid=l+r>>1;
tag[ls(p)]+=tag[p];
tag[rs(p)]+=tag[p];
tr[ls(p)]=(tr[ls(p)]+tag[p]*(mid-l+1))%mod;
tr[rs(p)]=(tr[rs(p)]+tag[p]*(r-mid))%mod;
tag[p]=0;
return;
}
void lazytag(int p,int l,int r,int pl,int pr,int k)
{
if(pl<=l&&pr>=r)
{
tr[p]=(tr[p]+k*(r-l+1));
tag[p]+=k;
return;
}
push_down(p,l,r);
int mid=l+r>>1;
if(pl<=mid) lazytag(ls(p),l,mid,pl,pr,k);
if(pr>mid)lazytag(rs(p),mid+1,r,pl,pr,k);
push_up(p);
return;
}
int query(int p,int l,int r,int pl,int pr)
{
int ans=0;
if(pl<=l&&pr>=r) return tr[p]%mod;
push_down(p,l,r);
int mid=l+r>>1;
if(pl<=mid) ans=(ans+query(ls(p),l,mid,pl,pr))%mod;
if(pr>mid) ans=(ans+query(rs(p),mid+1,r,pl,pr))%mod;
return ans;
}
void lazytag_way(int l,int r,int k)
{
k%=mod;
while(top[l]!=top[r])
{
if(dep[top[l]]<dep[top[r]]) swap(l,r);
lazytag(1,1,n,id[top[l]],id[l],k);
l=fa[top[l]];
}
if(dep[l]>dep[r]) swap(l,r);
lazytag(1,1,n,id[l],id[r],k);
return;
}
int query_way(int l,int r)
{
int ans=0;
while(top[l]!=top[r])
{
if(dep[top[l]]<dep[top[r]]) swap(l,r);
ans=(ans+query(1,1,n,id[top[l]],id[l]))%mod;
l=fa[top[l]];
}
if(dep[l]>dep[r]) swap(l,r);
ans=(ans+query(1,1,n,id[l],id[r]))%mod;
return ans;
}
void lazytag_subtree(int x,int k){lazytag(1,1,n,id[x],id[x]+len[x]-1,k);}
int query_subtree(int x){return query(1,1,n,id[x],id[x]+len[x]-1)%mod;}
signed main()
{
memset(h,-1,sizeof h);
n=read();
m=read();
r=read();
mod=read();
rep1(i,1,n) w[i]=read();
rep1(i,1,n-1)
{
int u=read();
int v=read();
add(u,v);
add(v,u);
}
dfs1(r,0,1);
dfs2(r,r);
build(1,1,n);
while(m--)
{
opt=read();
if(opt==1)
{
int x=read();
int y=read();
int z=read();
lazytag_way(x,y,z);
}
else if(opt==2)
{
int x=read();
int y=read();
cout<<query_way(x,y)<<endl;
}
else if(opt==3)
{
int x=read();
int z=read();
lazytag_subtree(x,z);
}
else
{
int z=read();
cout<<query_subtree(z)<<endl;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号