25.集合-Nim游戏 博弈论

 

 

 

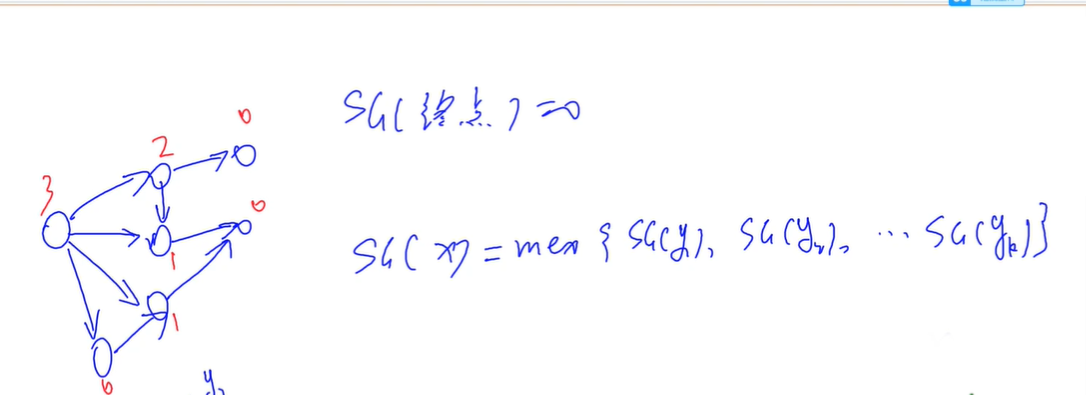
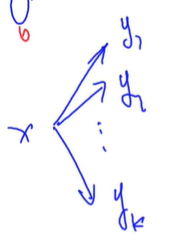
 SG(x) = 0，必败

SG(x) != 0，必胜

如果是多张图的话

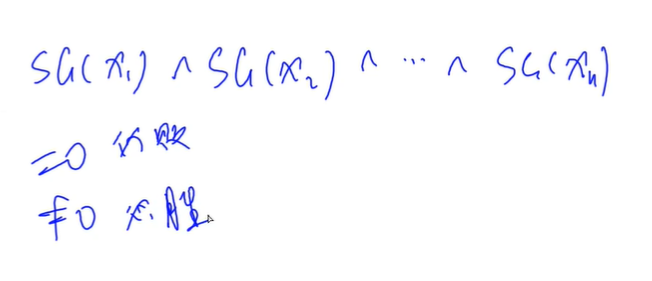
 石子堆数是10000，所以一共是10000个状态，枚举集合的个数是100

时间复杂度就是1e6

#include <bits/stdc++.h>
using namespace std;
const int N = 110, M = 10010;
int n, k;
int s[N], f[M];
//s存储给出的各个数
//f存储每堆石子的sg的值
int sg(int x) { 
    if (f[x] != -1) { //如果已经被算过了，不继续计算了，直接返回
        return f[x];
    }
    unordered_set<int> S; //存储当前这个局面能到的所有局面
    for (int i = 0; i < k; i++) { 
        int sum = s[i]; //现在sum[i]就是集合中的数，也就是可以取出的石子数
        if (x >= sum) {
            S.insert(sg(x - sum));
        }
    }
    for (int i = 0; ; i++) { //找到集合当中不存在的最小的自然数是多少
        if (!S.count(i)) {
            return f[x] = i;
        }
    }
}
int main() {
    cin >> k;
    for (int i = 0; i < k; i++) {
        cin >> s[i];
    }
    cin >> n;
    memset(f, -1, sizeof f); //用记忆化搜索来做
    int res = 0;
    for (int i = 0; i < n; i++) {
        int x;
        cin >> x;
        res ^= sg(x);
    }
    if (res) {
        cout << "Yes" << endl;
    } else {
        cout << "No" << endl;
    }
    return 0;
}