6.数字三角形

先来解释一下什么是线性dp

在求状态转移方程时，有明显的线性求取顺序

比如背包问题

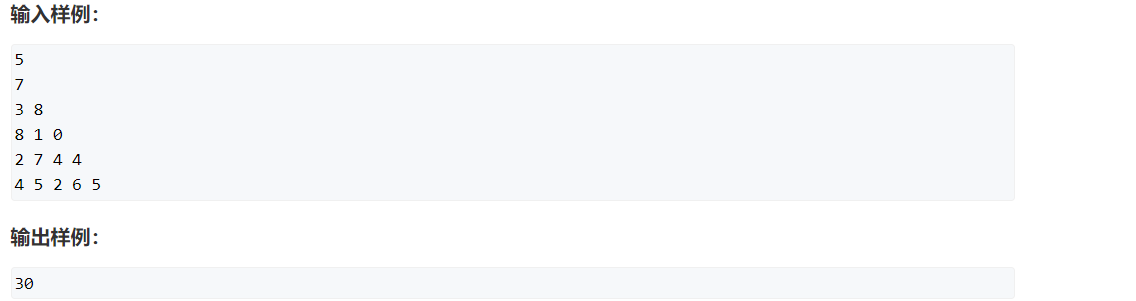
 这道题目我们先给数字编号

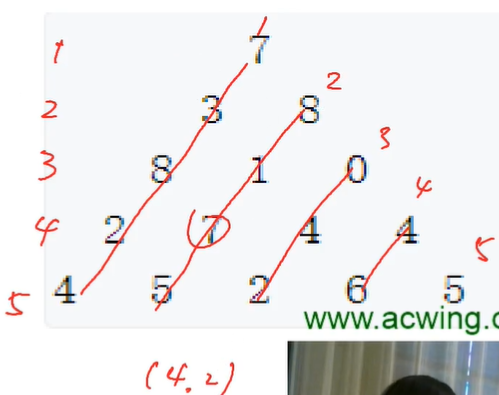
 分析

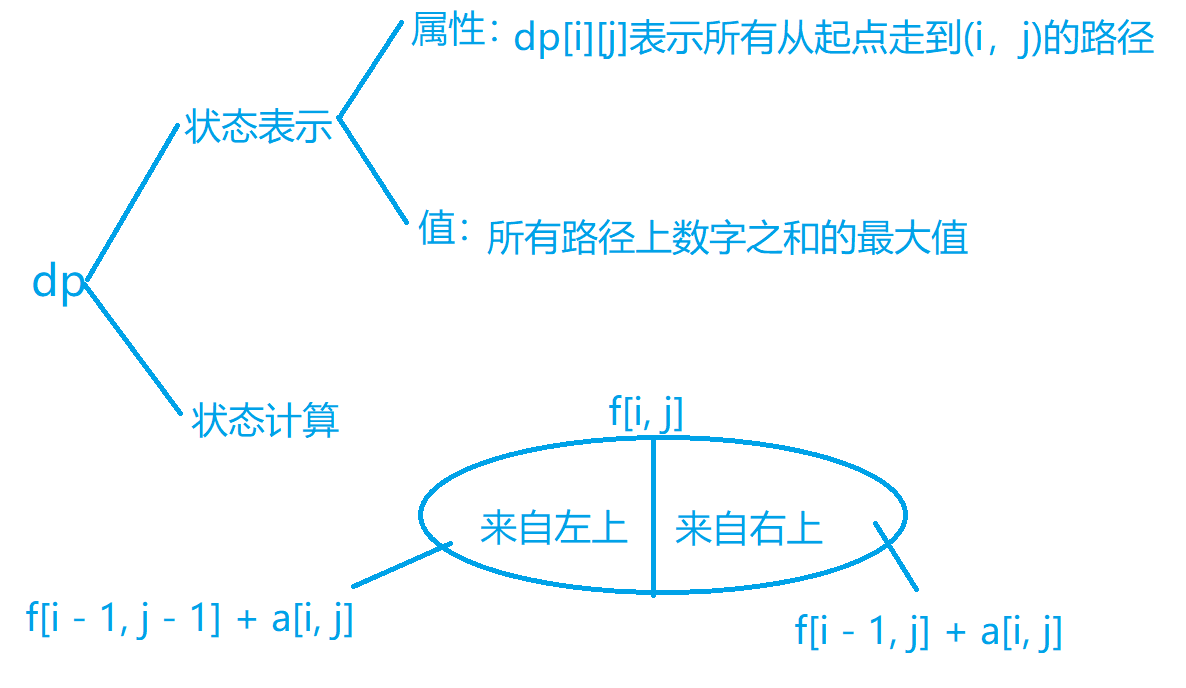
 dp问题的时间复杂度如何分析

一般是状态数量乘以转移的计算量（就是算每个状态需要的计算量）

本题大致就是500 * 500

#include <bits/stdc++.h>
using namespace std;
const int N = 510, INF = 1e9;
int a[N][N]; //存储三角形中的每一个点 
int dp[N][N];
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= i; j++) {
            cin >> a[i][j];
        }
    }
    for (int i = 1; i <= n; i++) { //全部初始化为-INF 
        for (int j = 0; j <= i + 1; j++) { //注意每行多初始化一个 
            dp[i][j] = - INF;
        }
    }
    dp[1][1] = a[1][1]; //边界 
    for (int i = 2; i <= n; i++) { //从第2行开始做 
        for (int j = 1; j <= i; j++) {
            dp[i][j] = max(dp[i - 1][j - 1] + a[i][j], dp[i - 1][j] + a[i][j]);
        }
    }
    int res = -INF;
    for (int i = 1; i <= n; i++) { //遍历最后一行找最大值 
        res = max(res, dp[n][i]);
    }
    cout << res << endl;
    return 0;
}