4.多重背包问题 II

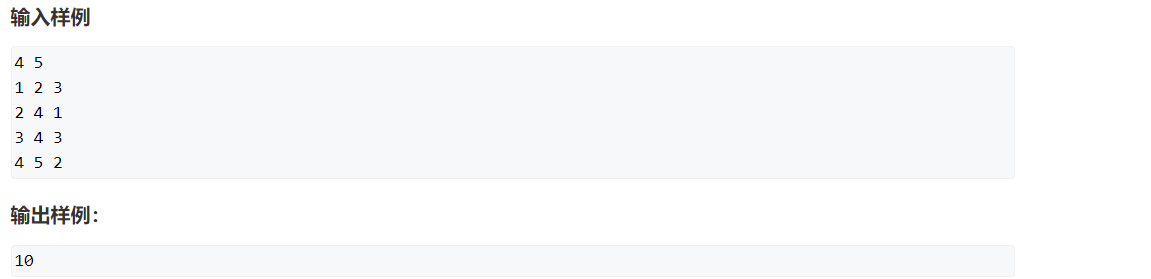
 当尝试用和完全背包问题相似的思路试图来优化的时候，就会发现优化不了

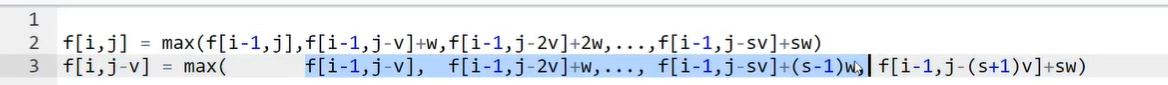
 用二进制优化

假设我们这件物品一共有1023个

我们真的需要从0到1到2一直枚举到1023吗

有没有一种更高效的方式来枚举呢

可以的

我们把若干个第i件物品打包在一起

打包成2的整次幂的形式

比如说10组

1， 2， 4， 8， ...，512

把第i个物品打包成10组

每一组最多只能选1次

2 ^ 10 = 1024

那么我们是否能用这10组拼凑出来从0到1023中的任何一个数呢

只用前1组，可以拼出0 ~ 1

只用前2组，可以拼出0 ~ 3

只用前3组，可以拼出0 ~ 7

只用前4组，可以拼出0 ~ 15

所以用前10组，可以凑出0 ~ 1023

然后每一个打包起来的第i个物品，可以看成是01背包中的一个物品，因为只可以选1次

就是说我们用10个新的物品，来表示我们的第i个物品

然后我们枚举这10个新的物品选或不选，就可以拼凑出来第i个物品的所有方案

原来需要枚举1024次，现在只需要10次

就是把1024转化为log 1024 = 10

 所以对于一个一般情况下的s

k是使得前面所有项相加之和小于等于s的最大的整次幂。

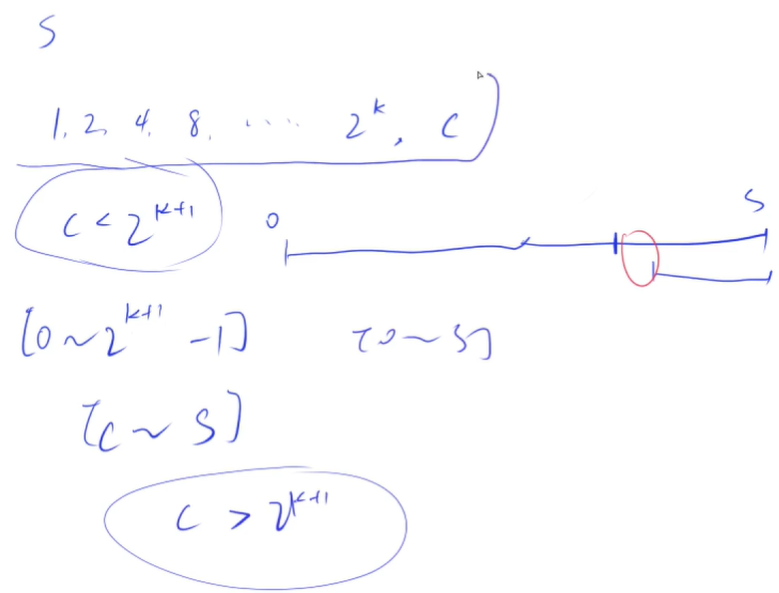
 这个k是最大的一个k使得1+2+4+8+...+2^k <= s

所以如果给我们第i个物品的数量是s的话

那么我们就可以把它拆成log s(向下取整)个组新的物品

新的物品每个最多只能用一次

所以我们先把所有的物品拆分，再对所有新出来的问题做一遍01背包

原来的三层循环时间复杂度是 n * v * s

现在是n * log s个物品的01背包问题

等于 n * log s * v = n * v * log s

所以对于本题就是1000 * 2000 * log 2000 = 2 * 10^6 * 11 = 2 * 10 ^ 7

#include <bits/stdc++.h>
using namespace std;
const int N = 11010;
//物品个数最多是1000 * log 2000
//log上取整 
int v[N], w[N];
int dp[N];
int main() {
    int n, m;
    cin >> n >> m;
    int cnt = 0; //新的物品的编号 
    for (int i = 1; i <= n; i++) {
        int a, b, s;
        //读入当前物品的体积，价值，数量 
        cin >> a >> b >> s;
        int k = 1; //从1开始分 
        while (k <= s) { //只要k<=s就可以分，每次把k个第i个物品打包在一起 
            cnt++; //编号++ 
            v[cnt] = a * k; //新物品的体积 
            w[cnt] = b * k; //新物品的价值 
            s -= k; // 
            k *= 2;
        }
        if (s > 0) { //这就是剩下的c 
            cnt++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    n = cnt;
    for (int i = 1; i <= n; i++) {
        for (int j = m; j >= v[i]; j--) {
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    cout << dp[m] << endl;
    return 0;
}