【线性代数】 矩阵消元

符号说明：  A      矩阵 

　　　　　  U      行阶梯形矩阵

　　　　      R      行最简形矩阵

消元(elimination)

示例：

 

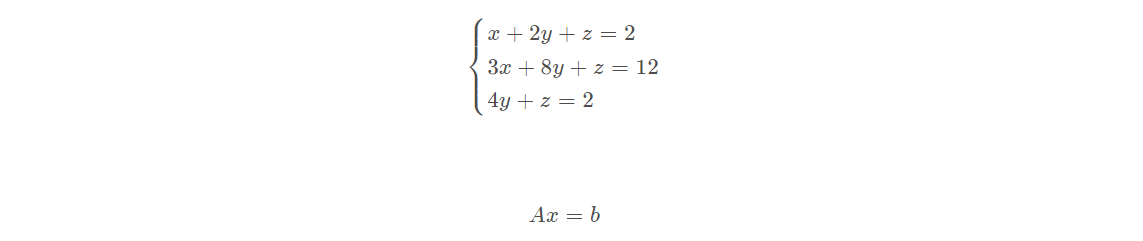
 对应矩阵：

 

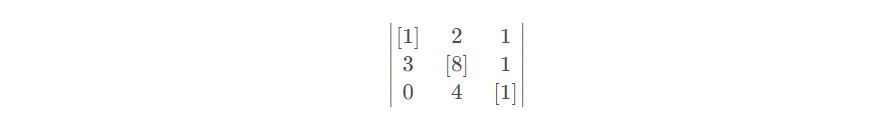
 首先消除第二行主元[1]：

 

 

　　第三行主元[1]已被消除，无需消元
　　接下来，消除第三行主元[2]
　　

 

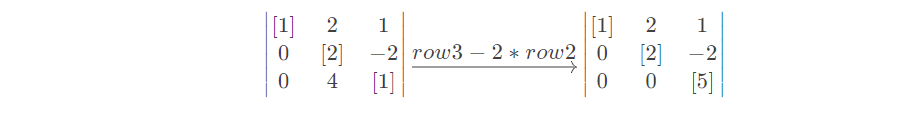
引入向量b（增广矩阵）进行消元，步骤与上面一致：

 

 　　最终消元结果为：

 

 

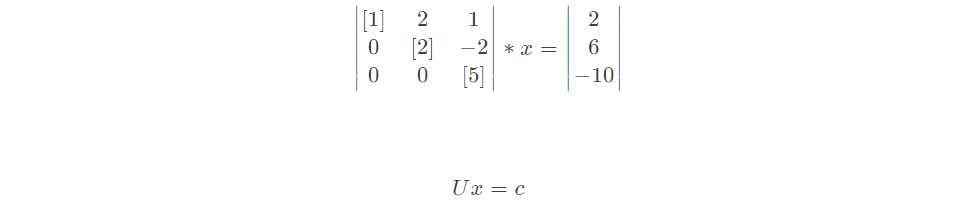
 注：主元必须不为零，但如果0占据了主元位置，则需要交换行使主元不为0，前提需要主元所在下行位置不能为0。如果主元为0，且无法与下行交换使之不为0，则矩阵不可逆，即消元失效。

回代(back substitution)

将以上消元的结果代入方程组：

 

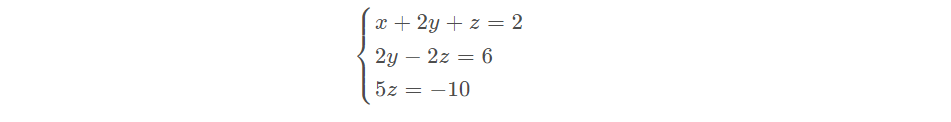
 得到

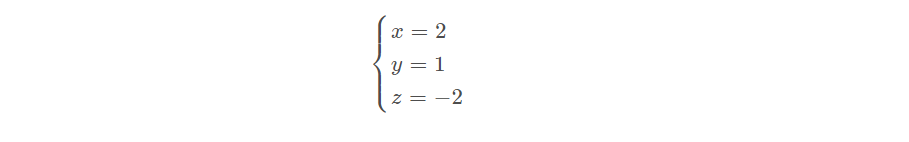
消元矩阵

根据：

 

 

 

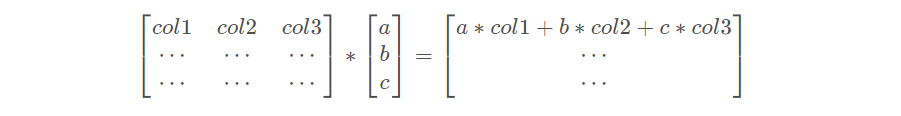
 得：

 

 

 

 

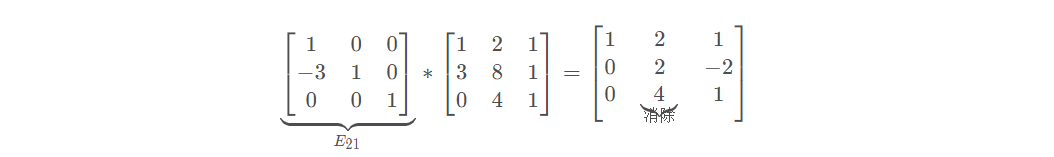
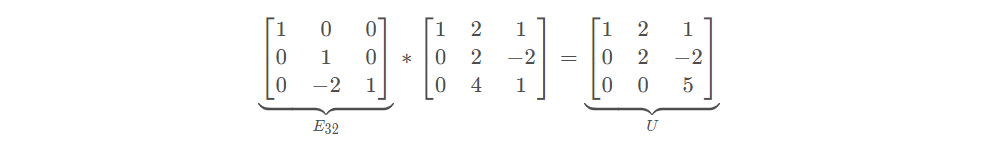
矩阵运算： E32​∗(E21​∗A)=U

 

 

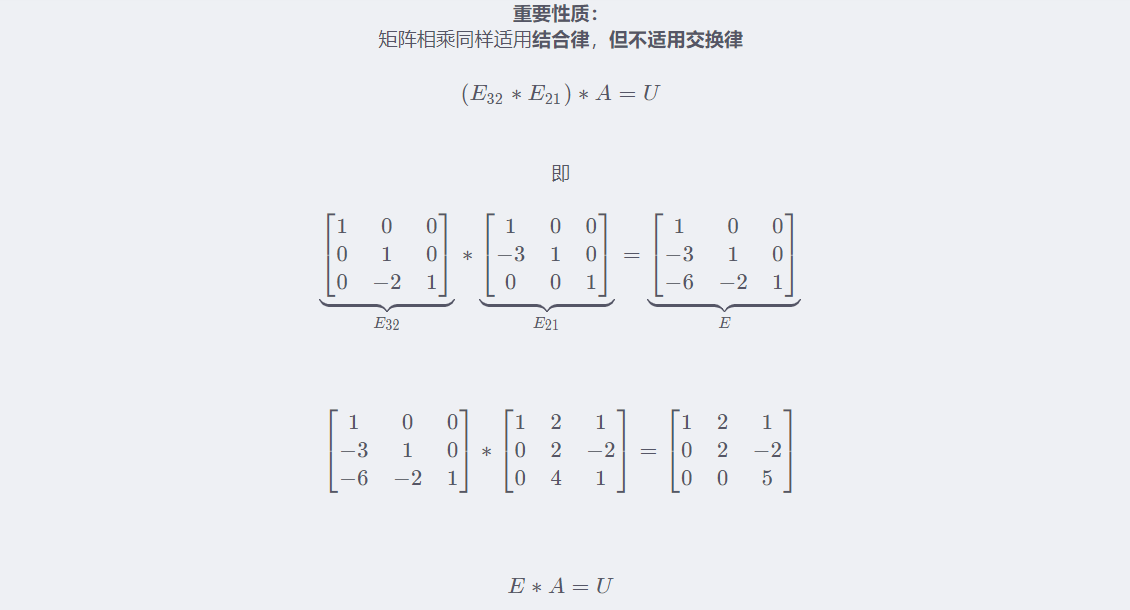
置换矩阵(permutation matrix)

行交换：

左乘交换了相应行的单位矩阵

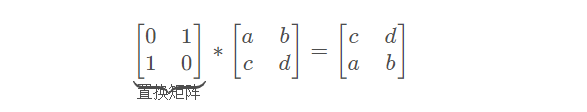
列交换：

右乘交换了相应列的单位矩阵