t1 2450距离链接：http://cogs.pro:8081/cogs/problem/problem.php?pid=vSNNNVqga

【题目描述】

在一个村子里有N个房子，一些双向的路连接着他们。人们总喜欢问这个“如果1想从房子A走到房子B有多远？”这个通常很难回答。但幸运的是在这个村里答案总是唯一的，自从道路修建以来这只有唯一的一条路（意思是你不能去一个地方两次）在每两座房子之间。你的工作是回答所有好奇的人。

【输入格式】

输入文件第一行有两个数n(2≤n≤10000)和m(1≤m≤20000),即房子数和问题数。后面n-1行每行由3个数构成i，j，k，由空格隔开，意思是房子i和房子j之间距离为k（0<k≤100）。房子以1到n标记。

下面m行每行有两个不同的整数i和j，你需要回答房子i和房子j之间的距离。

【输出格式】

输出有n行。每行表示个一个问题的答案。

【样例1】

输入样例1：
3 2
1 2 10
3 1 15
1 2
2 3
输出样例1：
10
25

【样例2】

输入样例2：
2 2
1 2 100
1 2
2 1
输出样例2：
100
100

思路：一道带边权的LCA，tarjan离线算法即可，将query读进来作为一种结构，同边一样记录，dfs的时候同时维护一个栈，栈元素的x为查询的from，i为边序号，维护这个栈即可，同时
　　距离dis[x]表示树根到x的距离，每次递归处理，ans[q[i].id]即为第几次询问的答案， 理解ans = dis_x + dis_y - 2 * dis_LCA，通过函数找到x和y的LCA
代码

  1 #define _CRT_SECURE_NO_WARNINGS
  2 #include "iostream"
  3 #include "cstdio"
  4 #include "cstring"
  5 #define maxn 10010
  6 using namespace std;
  7 int n, m, from, to, k;
  8 struct Edge
  9 {
 10     int to, val, pre;
 11 }e[maxn << 1];
 12 
 13 struct query
 14 {
 15     int to, id, pre;
 16 }q[maxn << 2];
 17 
 18 struct AA
 19 {
 20     int x, i;
 21 }a[maxn];
 22 
 23 int lastE[maxn] = { 0 };
 24 int lastQ[maxn] = { 0 };
 25 int p[maxn] = { 0 };
 26 int dis[maxn], anc[maxn], ans[maxn << 1];
 27 bool vis[maxn << 1] = { 0 };
 28 int cnt = 0, cnt1 = 0, cnt2 = 0, top = 0;
 29 
 30 void inserte(int from, int to, int val)
 31 {
 32     e[++cnt1].to = to;
 33     e[cnt1].val = val;
 34     e[cnt1].pre = lastE[from];
 35     lastE[from] = cnt1;
 36 }
 37 
 38 void insertq(int from, int to, int i)
 39 {
 40     q[++cnt2].to = to;
 41     q[cnt2].id = i;
 42     q[cnt2].pre = lastQ[from];
 43     lastQ[from] = cnt2;
 44 }
 45 
 46 int findRoot(int x)
 47 {
 48     static int y, root;
 49     root = anc[x];
 50     while (anc[root] != root)
 51         root = anc[root];
 52     while (anc[x] != x)
 53     {
 54         y = anc[x];
 55         anc[x] = root;
 56         x = y;
 57     }
 58     return root;
 59 }
 60 
 61 void dfs(int x)
 62 {
 63     int y, i;
 64     a[++top].x = x;
 65     a[top].i = lastE[x];
 66     while (top)
 67     {
 68         x = a[top].x;
 69         i = a[top].i;
 70         if (e[i].to == p[x])
 71             i = e[i].pre;
 72         if (i)
 73         {
 74             a[top].i = e[i].pre;
 75             y = e[i].to;
 76             p[y] = x;
 77             dis[y] = dis[x] + e[i].val;
 78             a[++top].x = y;
 79             a[top].i = lastE[y];
 80             anc[y] = y;
 81          }
 82         else
 83         {
 84             vis[x] = 1;
 85             for (int i = lastQ[x]; i; i = q[i].pre)
 86             {
 87                 y = q[i].to;
 88                 if (vis[y])
 89                 {
 90                     ans[q[i].id] = dis[x] + dis[y] - (dis[findRoot(y)] << 1);
 91                 }
 92             }
 93             anc[x] = p[x];
 94             top--;
 95         }
 96     }
 97 }
 98 
 99 
100 
101 
102 int main()
103 {
104     freopen("distance.in", "r", stdin);
105     freopen("distance.out", "w", stdout);
106     scanf("%d%d", &n, &m);
107     for (int i = 0; i < n - 1; i++)
108     {
109         scanf("%d %d %d", &from, &to, &k);
110         inserte(from, to, k);
111         inserte(to, from, k);
112     }
113     for (int i = 0; i < m; i++)
114     {
115         scanf("%d %d", &from, &to);
116         insertq(from, to, i);
117         insertq(to, from, i);
118     }
119     dis[1] = p[1] = 0;
120     dfs(1);
121     
122     for (int i = 0; i < m; i++)
123         printf("%d\n", ans[i]);
124     return 0;
125 }

t2 cogs 1588 题目链接：http://cogs.pro:8081/cogs/problem/problem.php?pid=vxmxQkgUU

【题目描述】

农夫约翰有N（2<=N<=40000）个农场，标号1到N。M（2<=M<=40000）条的不同的垂直或水平的道路连结着农场，道路的长度不超过1000.这些农场的分布就像下面的地图一样，图中农场用F1..F7表示：

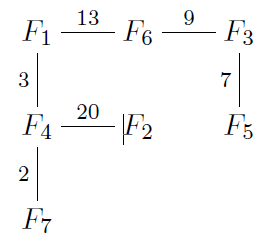
每个农场最多能在东西南北四个方向连结4个不同的农场。此外，农场只处在道路的两端。道路不会交叉而且每对农场间有且仅有一条路径。邻居鲍伯要约翰来导航，但约翰丢了农场的地图，他只得从电脑的备份中修复率。每一条道路的信息如下：

从农场23往南经距离10到达农场17

从农场1往东经距离7到达农场17

. . .

最近美国过度肥胖非常普遍。农夫约翰为了让他的奶牛多做运动，举办了奶牛马拉松。马拉松路线要尽量长。

奶牛们拒绝跑马拉松，因为她们悠闲的生活无法承受约翰选择的如此长的赛道。因此约翰决心找一条更合理的赛道。他打算咨询你。读入地图之后会有K个问题，每个问题包括2个整数，就是约翰感兴趣的2个农场的编号，请尽快算出这2个农场间的距离。

【输入格式】

第1行：两个分开的整数N和M。

第2到M+1行：每行包括4个分开的内容，F1,F2,L,D分别描述两个农场的编号，道路的长度，F1到F2的方向N,E,S,W。

第2+M行：一个整数K（1<=K<=10000）.

第3+M到2+M+K行：每行输入2个整数，代表2个农场。

【输出格式】

对每个问题，输出单独的一个整数，给出正确的距离。

【样例输入】

【样例输出】

13
3
36

【提示】

农场2到农场6有20+3+13=36的距离。

同t1，读入的时候读方向但是忽略即可。

代码：

  1 #define _CRT_SECURE_NO_WARNINGS
  2 #include "iostream"
  3 #include "cstdio"
  4 #include "cstring"
  5 #define maxn 40010
  6 using namespace std;
  7 int n, m, from, to, k, sumQ;
  8 struct Edge
  9 {
 10     int to, val, pre;
 11 }e[maxn << 1];
 12 
 13 struct query
 14 {
 15     int to, id, pre;
 16 }q[maxn << 2];
 17 
 18 struct AA
 19 {
 20     int x, i;
 21 }a[maxn];
 22 
 23 int lastE[maxn] = { 0 };
 24 int lastQ[maxn] = { 0 };
 25 int p[maxn] = { 0 };
 26 int dis[maxn], anc[maxn], ans[maxn << 1];
 27 bool vis[maxn << 1] = { 0 };
 28 int cnt = 0, cnt1 = 0, cnt2 = 0, top = 0;
 29 
 30 void inserte(int from, int to, int val)
 31 {
 32     e[++cnt1].to = to;
 33     e[cnt1].val = val;
 34     e[cnt1].pre = lastE[from];
 35     lastE[from] = cnt1;
 36 }
 37 
 38 void insertq(int from, int to, int i)
 39 {
 40     q[++cnt2].to = to;
 41     q[cnt2].id = i;
 42     q[cnt2].pre = lastQ[from];
 43     lastQ[from] = cnt2;
 44 }
 45 
 46 int findRoot(int x)
 47 {
 48     static int y, root;
 49     root = anc[x];
 50     while (anc[root] != root)
 51         root = anc[root];
 52     while (anc[x] != x)
 53     {
 54         y = anc[x];
 55         anc[x] = root;
 56         x = y;
 57     }
 58     return root;
 59 }
 60 
 61 void dfs(int x)
 62 {
 63     int y, i;
 64     a[++top].x = x;
 65     a[top].i = lastE[x];
 66     while (top)
 67     {
 68         x = a[top].x;
 69         i = a[top].i;
 70         if (e[i].to == p[x])
 71             i = e[i].pre;
 72         if (i)
 73         {
 74             a[top].i = e[i].pre;
 75             y = e[i].to;
 76             p[y] = x;
 77             dis[y] = dis[x] + e[i].val;
 78             a[++top].x = y;
 79             a[top].i = lastE[y];
 80             anc[y] = y;
 81         }
 82         else
 83         {
 84             vis[x] = 1;
 85             for (int i = lastQ[x]; i; i = q[i].pre)
 86             {
 87                 y = q[i].to;
 88                 if (vis[y])
 89                 {
 90                     ans[q[i].id] = dis[x] + dis[y] - (dis[findRoot(y)] << 1);
 91                 }
 92             }
 93             anc[x] = p[x];
 94             top--;
 95         }
 96     }
 97 }
 98 
 99 
100 
101 
102 int main()
103 {
104     freopen("dquery.in", "r", stdin);
105     freopen("dquery.out", "w", stdout);
106     char c;
107     scanf("%d%d", &n, &m);
108     for (int i = 0; i < m; i++)
109     {
110         scanf("%d %d %d %c", &from, &to, &k, &c);
111         inserte(from, to, k);
112         inserte(to, from, k);
113     }
114     scanf("%d", &sumQ);
115     for (int i = 0; i < sumQ; i++)
116     {
117         scanf("%d %d", &from, &to);
118         insertq(from, to, i);
119         insertq(to, from, i);
120     }
121     dis[1] = p[1] = 0;
122     dfs(1);
123 
124     for (int i = 0; i < sumQ; i++)
125         printf("%d\n", ans[i]);
126     return 0;
127 }

t3 cogs

2084. [SYOI 2015] Asm.Def的基本算法

链接：http://cogs.pro:8081/cogs/problem/problem.php?pid=vyiJNVaUq

【题目描述】

“有句美国俗语说，如果走起来像鸭子，叫起来像鸭子，那就是一只鸭子。”斯科特·华莱士看着Asm.Def面前屏幕上滚动的绿色字符，若有所思地说。

“什么意思？”

“你的数据。看上去是一棵树。”

“按照保密条令，我什么也不说这是最好的——但见你这么热情，一句话不说也不好。”Asm.Def停下手中的快速数论变换，“确实是树。”

“然后你怎么算出来目标的位置？”

“都需要按照基本算法，按照图论的那一套理论，去产生。听说过LCA吗？不是那个印度飞机，我是说最近公共祖先……

Asm.Def通过分析无线电信号得到了一棵有n个节点，以1为根的树。除1之外，节点i的父亲是p_i。节点带有权值，节点i的权值是w_i。

我们定义某点的祖先为从根到它路径上的所有点（包括它本身），而两个节点a、b的最近公共祖先是某个点p，使得p同时是a、b的祖先，而且p离根最远。

Asm.Def想要求出

（文字：∑∑w_i*w_j*w_LCA(i,j)），

其中LCA(i,j)是i、j的最近公共祖先，他认为这个值至关重要。由于这个值可能很大，Asm.Def只需要知道它模1,000,000,007（即10^9+7）的结果。

【输入格式】

第1行两个整数：n和w_1.

第2行到第n行，第i行有两个整数p_i和w_i。

【输出格式】

一行一个整数，即答案模1,000,000,007的值。

【样例输入】

2 2
1 1

【样例输出】

【提示】

1×1×1+1×2×2+2×1×2+2×2×2=17。

对于30%的数据，n<=100，w_i<=10。

对于60%的数据，n<=1000，w_i<=1000.

对于100%的数据，1<=n<=10^5，0<=w_i<=10^9，1<=p_i<i.

思路：递归遍历，以每个节点为一个根为单位，维护以此节点为根的子树的权值sum，乘积求和，见注释

代码：

 1 #define _CRT_SECURE_NO_WARNINGS
 2 #include "iostream"
 3 #include "cstdio"
 4 #include "cstring"
 5 
 6 #define ll long long
 7 #define maxn 100100
 8 using namespace std;
 9 
10 struct Edge
11 {
12     ll to, pre;
13     Edge() :to(), pre(0) {};
14 }e[maxn << 2];
15 bool vis[maxn << 1];
16 int prt[maxn], n, w[maxn], last[maxn << 1];
17 int cnt = 0;
18 ll sum = 0;
19 int s[maxn];                                          //以x为根的点的权值和
20 //int sz[maxn];                                         //子孙节点个数
21 
22 void insert(int from, int to)
23 {
24     e[++cnt].to = to;
25     e[cnt].pre = last[from];
26     last[from] = cnt;
27 }
28 
29 void dfs(int x)
30 {
31     //sz[x] = 1;                                        //从x开始，子孙节点个数为1
32     s[x] = w[x];                                      //包含自己，子节点权值和为w_x
33     int y;
34     for (int i = last[x]; i; i = e[i].pre)
35     {
36         y = e[i].to;
37         if (y == prt[x])
38             continue;
39         prt[y] = x;
40         dfs(y);
41         s[x] = (s[x] + s[y]) % 1000000007;             //回溯后，子节点和累加上来
42         //sz[x] += sz[y];                               //子节点个数累加
43     }
44 
45     ll ss = s[x], tmp = 0;
46     for (int i = last[x]; i; i = e[i].pre)
47     {
48         y = e[i].to;
49         if (y == prt[x])
50             continue;
51         //ss-s_y即为除了y和它的子节点权值和 其余节点的权值和，乘积满足Σwi*wj
52         tmp = (tmp + ((ll)s[y] * ((ss - s[y] + 1000000007) % 1000000007) % 1000000007)) % 1000000007;
53         //每个乘积会被算两次但父节点和子节点不会，因此再加上s_y * wx
54         tmp = (tmp + ((ll)s[y] * w[x] % 1000000007)) % 1000000007;
55     }
56     //对每个x，都有i==j的时候，x和自己的乘积以及LCA也是它自己
57     tmp = (tmp + ((ll)w[x] * w[x] % 1000000007)) % 1000000007;
58     //前边只有wi wj，统一乘wLCA
59     tmp = ((ll)tmp * w[x]) % 1000000007;
60     sum = (sum + tmp) % 1000000007;
61 }
62 
63 int main()
64 {
65     freopen("asm_algo.in", "r", stdin);
66     freopen("asm_algo.out", "w", stdout);
67     int x, y;
68     scanf("%d %d", &n, &w[1]);
69     for (int i = 2; i <= n; i++)
70     {
71         scanf("%d %d", &x, &y);
72         w[i] = y;
73         insert(x, i);
74     }
75     
76     dfs(1);
77     printf("%lld\n", sum);
78     return 0;
79 }

posted on 2019-10-29 17:30 kxxy 阅读(281) 评论(0) 收藏举报

刷新页面返回顶部