负数和小数点在计算机中的二进制表示
一、负数的表示:
在计算机中,负数以其正值的补码形式表示,补码为该数的反码加一。以下是补码的概念。
1.源码
一个整数,按照绝对值大小转换成的二进制数,称为原码。
在4字节中,0110 是 6 的原码。
2.反码
将二进制数按位取反,所得的新二进制数称为原二进制数的反码。
0110 的反码是 1001
3.补码
二进制的反码加1,得到该二进制数的补码,1010则为6在二进制中的补码
1001 的补码是 1010
4.负数运算
在二进制中计算5-3,减号表示为加该二进制数的补码
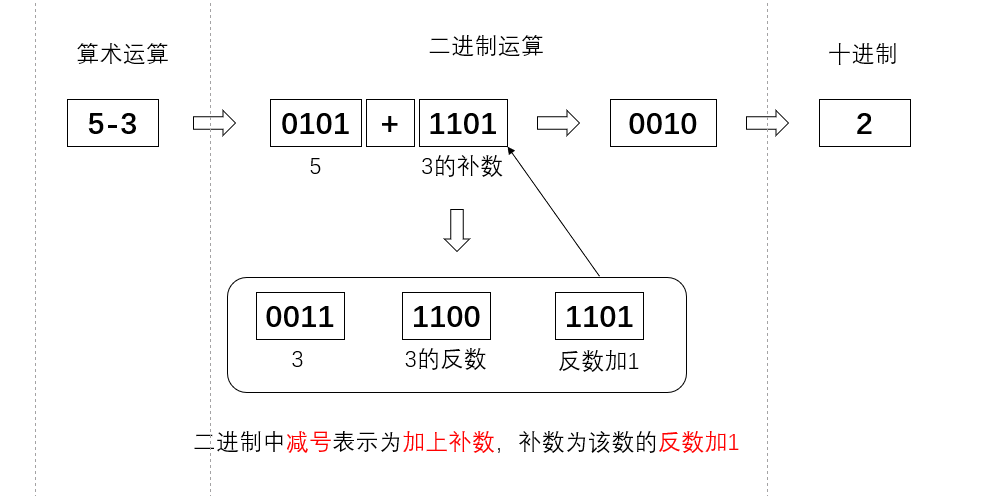
5.补码为何是反码+1
- 计算机的补码也相当于算术里的补数
要了解补数,首先该了解模的概念。模是指一个计量系统的计数范围,如时钟等,它的计量范围是0~11,模 = 12。计算机也是有一个计量范围,即都存在一个“模”,32位计算机的计量范围是2^32,模 = 2^32。“模”是计量器产生“溢出”的量,它的值在计量器上表示不出来,在12小时的时钟里,12点就是0点。
- 补数:二者相加等于模的数为补数
在以模为12的系统中,加9和减3效果是一样的,因此凡是减3运算,都可以用加9来代替。对“模”12而言,9和3互为补数(二者相加等于模)。
所以我们可以得出一个结论,即在有模的计量系统中,减一个数等于加上它的补数,从而实现将减法运算转化为加法运算的目的。
# 按以上理论,减一个数等于加上它的补数,所以 5 - 3 # 在4位字节,模=16 5 + (16 - 3) //模减去3则为3的补数 # 用二进制表示则为: 0101 + (10000 - 0011) # 等价于 0101 + ((1 + 1111) - 0011) # 等价于 0101 + (1 + (1111 - 0011)) # 等价于 0101 + (1 + 1100) // 括号内是3(0011)的反码+1,正是补码的定义 # 等价于 0101 + 1101 # 所以从这里可以得到 -3 = 1101 # 即 `-3` 在计算机中的二进制表示为 `1101`,正是“ -3 的正值 3(`0011`)的补码(`1101`)”。 # 最后一步 0101 + 1101 等于10010 #在4位字节中为0010
二、小数点的表示:
1.浮点数表示
-
IEEE754 标准
计算机是无法识别 . 号的,那么二进制小数中的点需要被保存下来,它是如何保存的呢?
1985年,随着
IEEE标准754的推出,制定出了浮点数的统一表示以及运算的标准
目前,所有的计算机都支持这个标准,为科学应用程序在不同机器上的可移植性鉴定了基础
-
标准公式
V = (-1)s * M * 2E 或 V=(-1)sign * mantissa * base * exponent
s:符号 s取1时代表负,取0代表正
m:尾数 小数点后面的数,1< m < base,在二进制中,m永远 1 < m <2
e:指数 以10为底的指数
base:进制数/基数,在计算机中一般为2
-
转换例子
例如16.125
十进制转换为二进制,整数位与小数位分开转换,16转为10000
0.125采用新的转换二进制方法,如下:
将小数位不断乘2,每次取其整数部位数的0或1,直到小数位变成0 0.125 * 2 =0.25 ———> 0 0.250 * 2 =0.50 ———> 0 0.500 * 2 =1.00 ———> 1
得出0.125二进制表示为001,因此16.125二进制表示为10000.001
使用IEEE754标准表示为 16.125=1.0000001*24
1.0000001为尾数,2为基数,4为指数
2.浮点数存储
-
单精度浮点数
以float类型为例,它是单精度存储类型,占4个字节,一个字节有8位,因为它占32位内存空间
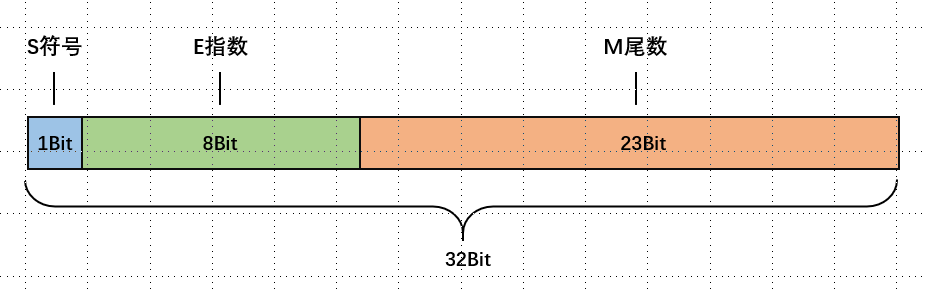
将16.125=10000.001=1.0000001*24的二进制存储到float中,s为0,E为4,M为1.0000001
值得注意的是,指数E有一个偏移值为127,正数则是加,负数则减;尾数M因在二进制中始终 1< M <2,所以M的第一位数永远为1,需在计算机中省略掉
指数127+4=131转为二进制10000011,尾数为0000001,需补齐23位,填入内存中为:

单精度类型float的取值范围是-3.4e38~3.4e38,有效数字为7,由于最高位不为1,可能是8
-
双精度浮点数
以double类型为例,它是双精度存储类型,占8个字节,拥有64位内存
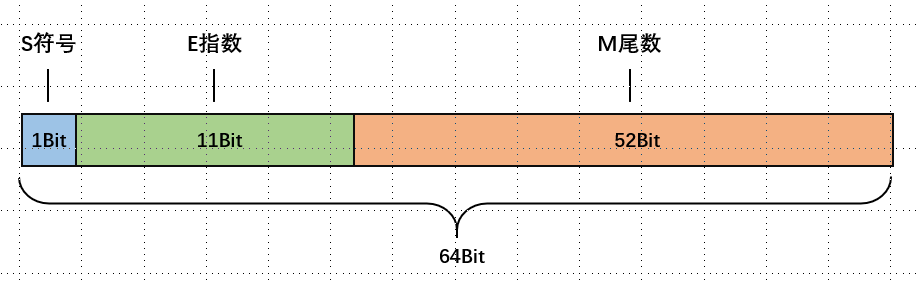
其存储方式与单精度相同,只是存储的大小和精度有所改变
双精度类型float的取值范围是-1.7e308~1.7e208,有效数字为15~16
3.定点数与浮点数区分
计算机中常用的数据表示格式有两种,一是定点格式,二是浮点格式,浮点格式应用较多
- 定义
定点数和浮点数,是指在计算机中一个数的小数点的位置是固定的还是浮动的
- 区分
1.如果一个数中小数点的位置是固定的,则为定点数;如果一个数中小数点的位置是浮动的,则为浮点数
2.定点格式可表示的数值的范围有限,但要求的处理硬件比较简单。而浮点格式可表示的数值的范围很大,但要求的处理硬件比较复杂
3.采用定点数表示法的计算机称为定点计算机,采用浮点数表示法的计算机称为浮点计算机。定点机在使用上不够方便,但其构造简单,造价低,一般微型机和单片机大多采用定点数的表示方法。浮点机可表示的数的范围比定点机大得多,使用也比较方便,但是比定点机复杂,造价高,在相同的条件下浮点运算比定点运算速度慢
- 表示法
通常将定点数据表示成纯小数或纯整数。为了将数表示成纯小数,通常把小数点固定在数值部分的最高位之前;而为了把数表示成纯整数,则把小数点固定在数值部分的最后面
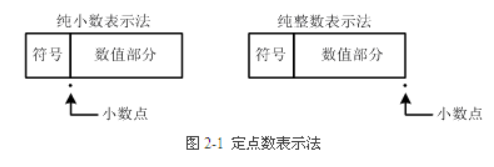
三、总结
1.负数在计算机中以补码形式存储,补码类似算术里的补数,二进制中补码为反码+1
2.小数点在计算机中以浮点形式存储,采用国际通用IEEE754标准,公式为V = (-1)s * M * 2E
3.除了浮点数还需要了解有定点数,顾名思义,小数点位置固定。
参考原文:https://blog.csdn.net/leonliu06/article/details/78685248
https://blog.csdn.net/baidu_35812312/article/details/79203971



 浙公网安备 33010602011771号
浙公网安备 33010602011771号