AIGC拾遗:SDE视角下的DDPM和score-based model
背景
本文尝试从SDE的视角下,统一DDPM和score-based model。
SDE
假设前向SDE过程为
考虑到实际情况下,\(f(x_{t}, t)\)只与\(x_{t}\)的一次项相关,因此上述公式可以改写为
其中,\(f(x_{t}, t)\)称为漂移系数,\(g(t)\)称为扩散系数。
逆向SDE
假设前向SDE过程为
其逆向SDE为
通过求解得分函数\(\nabla_{x_{t}}\log{p_{t}(x_{t})}\),即可通过逆向SDE过程生成样本。
前向扩散
无论是DDPM还是score-based model,前向扩散过程都能够写成
此时,\(x_{t} \sim \mathcal{N}(\alpha_{t}x_{0}, \sigma_{t}^{2}I)\)
均值与方差
我们想要通过\(\alpha_{t}\)和\(\sigma_{t}\)计算得到\(f(t)\)和\(g(t)\),可以借助方差与均值进行计算。
均值
\(\mathbb{E}[dx_{t}]=\mathbb{E}[f(t)x_{t}dt+g(t)dw_{t}]=f(t)\mathbb{E}[x_{t}]dt\),即
由前向扩散公式可知,\(\mathbb{E}[x_{t}]=\alpha_{t}x_{0}\),因此
方差
考虑到\(dVar[x_{t}]=d(\mathbb{E}[x^{2}_{t}]-\mathbb{E}^{2}[x_{t}])\)
- \(d(\mathbb{E}[x_{t}^{2}])=\mathbb{E}[dx_{t}^{2}]=\mathbb{E}[2x_{t}dx_{t}+(dx_{t})^{2}]\)
- \(d(\mathbb{E}^{2}[x_{t}])=2\mathbb{E}[x_{t}]d(\mathbb{E}[x_{t}])=2\mathbb{E}[x_{t}]\mathbb{E}[d(x_{t})]=2f(t)\mathbb{E}^{2}[x_{t}]dt\)
因此,
由前向扩散可得,\(Var[x_{t}]=\sigma_{t}^{2}\),因此
VE-SDE
对于score-based model,前向加噪过程为
其方差是逐步增大的,称为VE-SDE。前向加噪过程中的\(\alpha_{t}=1\),因此,对应的前向SDE为
VP-SDE
对于DDPM,前向加噪过程为
且\(\bar{\alpha}_{t}^{2}+\sigma_{t}^{2}=1\),其方差是有限的,称为VP-SDE。代入可得
为了对齐原始DDPM的加噪方式:\(x_{t+1}=\sqrt{1-\beta_{t}}x_{t}+\sqrt{\beta_{t}}\epsilon\),我们需要计算\(\bar{\alpha}_{t}\)与\(\beta_{t}\)的关系。
因此,DDPM的前向SDE为
逆向扩散
考虑到逆向SDE过程
对应的离散化过程为
对于VP-SDE,代入上式可得逆向采样过程为
\[x_{t-1}=(1+\frac{1}{2}\beta_{t})x_{t}+\beta_{t}s_{\theta}(x_{t}, t)+\sqrt{\beta_{t}}\epsilon \]进一步近似后\((1+\frac{1}{2}\beta_{t})\sim\frac{1}{\sqrt{1-\beta_{t}}}\),\(s_{\theta}(x_{t}, t)=-\frac{\epsilon_{\theta}(x_{t}, t)}{\sqrt{1-\bar{\alpha}_{t}}}\)可得
\[x_{t-1}=\frac{1}{\sqrt{1-\beta_{t}}}[x_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon_{\theta}(x_{t}, t)]+\sqrt{\beta_{t}}\epsilon \]这与DDPM中的采样公式一致。
对于VE-SDE,代入上式可得逆向采样过程为
\[x_{t-1}=x_{t}+(\sigma_{t}^{2}-\sigma_{t-1}^{2})s_{\theta}(x_{t}, t)+\sqrt{\sigma_{t}^{2}-\sigma_{t-1}^{2}}\epsilon \]
总结
本文在SDE的视角下,统一了DDPM与score-based model,可以由如下两图概括。
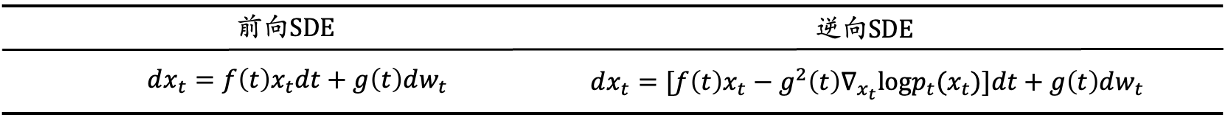





 浙公网安备 33010602011771号
浙公网安备 33010602011771号