仿射密码

前言

在密码学的发展历程中，从简单的凯撒密码到更具安全性的加密方式，仿射密码是重要的进阶。它基于数论知识，通过线性变换为信息加密，既保留了替换加密的简洁，又大幅提升了保密性，是理解现代加密算法的关键基础之一。

一、 数论

在正式介绍仿射密码之前，我们需要了解一些数论知识。为我们后面的学习有更好的基础。

1.1 数论的概念

这里我们主要说的是初等数论，其是数论的一个分支。一般说来，指用算术推导方法论证数论命题的分支学科。

1.2 算术基本定理

算术基本定理可表述为：任何一个大于1的自然数 N,如果N不为质数，那么N可以唯一分解成有限个质数的乘积。即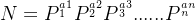
，这里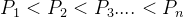
均为质数，其中指数是正整数。这样的分解称为N 的标准分解式。
定理的应用：
一个大于1的正整数N，如果它的标准分解式为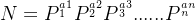：，那么它的正因数个数为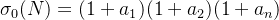
它的全体正因数之和为

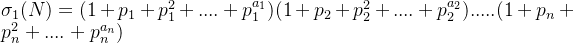
对于该定理我们可以使用python进行实现：

点击查看代码

def prime(n):
    factor = []
    for i in range(2,n+1):  # 从2开始遍历到n
        while n % i == 0:   # 如果n能被i整除
            factor.append(i)     # 把i加入因子列表
            n = n // i       # 把n除以i的商赋值给n
        if n == 1:
            break
    return factor
 
 
print(prime(30))

1.3 欧几里得算法

欧几里得算法又称辗转相除法，是指用于计算两个正整数a，b的最大公约数。计算公式为gcd(a,b) = gcd(b,a mod b)。
两个整数的最大公约数是能够同时整除它们的最大的正整数。辗转相除法基于如下原理：两个整数的最大公约数等于其中较小的数和两数相除余数的最大公约数。
将其编写为python语言为：

点击查看代码

def gcd(m,n):
    if(m % n == 0):
        return n
    else:
        return gcd(n,m % n)

1.4 扩展欧几里得算法

除了计算a、b两个整数的最大公约数，此算法还能找到整数x、y（其中一个很可能是负数）。通常谈到最大公因子时，我们都会提到一个非常基本的事实: 给予二整数a与b，必存在有整数x与y使得ax+by=gcd（a，b）。有两个数a,b，对它们进行辗转相除法，可得它们的最大公约数——这是众所周知的。然后，收集辗转相除法中产生的式子，倒回去，可以得到ax+by=gcd(a,b)的整数解。
例：求5x1(mod 18)

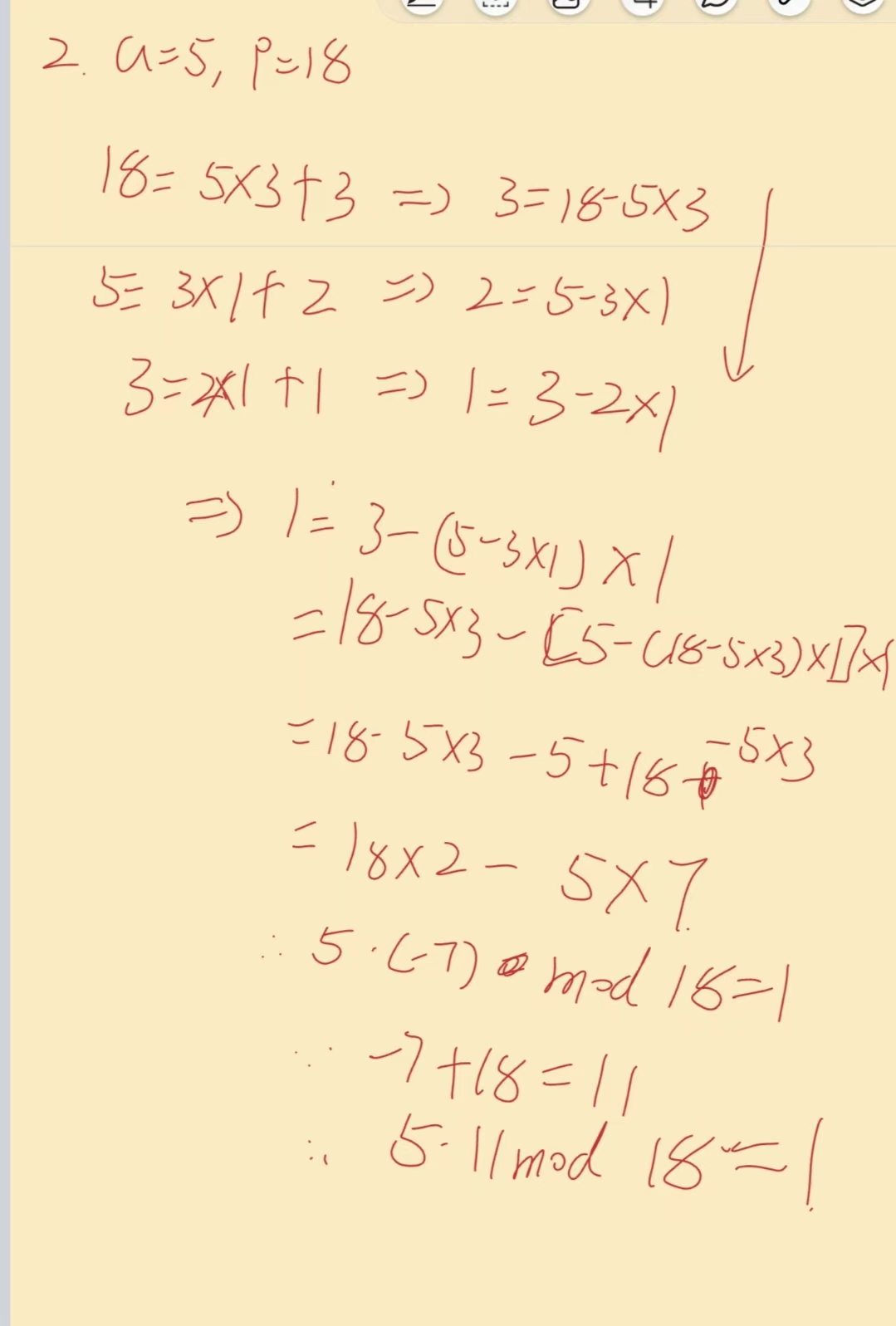
扩展欧几里得算法可以用来计算模逆元，而模反元素在RSA加密算法中有很重要的地位。用代码实现：

点击查看代码

def gcd(a,b):
    if a == 0:
        return b,0,1
    else:
        gcd1,x,y = gcd(b%a,a)
        return gcd1,y - (b//a) * x,x

1.5 孙子定理

孙子定理是中国古代求解一次同余式组的方法。是数论中一个重要定理。又称中国剩余定理。
孙子定理是初等数论中的一个重要定理，凝结着中国古代数学家的智慧，在加密、秘密共享、数字签名等领域都有重要应用。
用现代数学的语言来说明的话，中国剩余定理给出了以下的一元线性同余方程组：

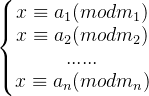
有解的判定条件，并用构造法给出了在有解情况下的具体形式。
中国剩余定理说明：假设整数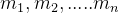两两互质，则对任意的整数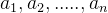,方程组（S）有解，并且通解可以为：

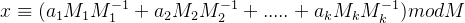
其中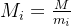
在此之前，我们需要了解几个知识点：

• a mod b = (a+k*b) mod b
• (a * k) mod b = k * (a mod b)
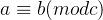• 的意思是a mod c = b mod c
  例：
  
  
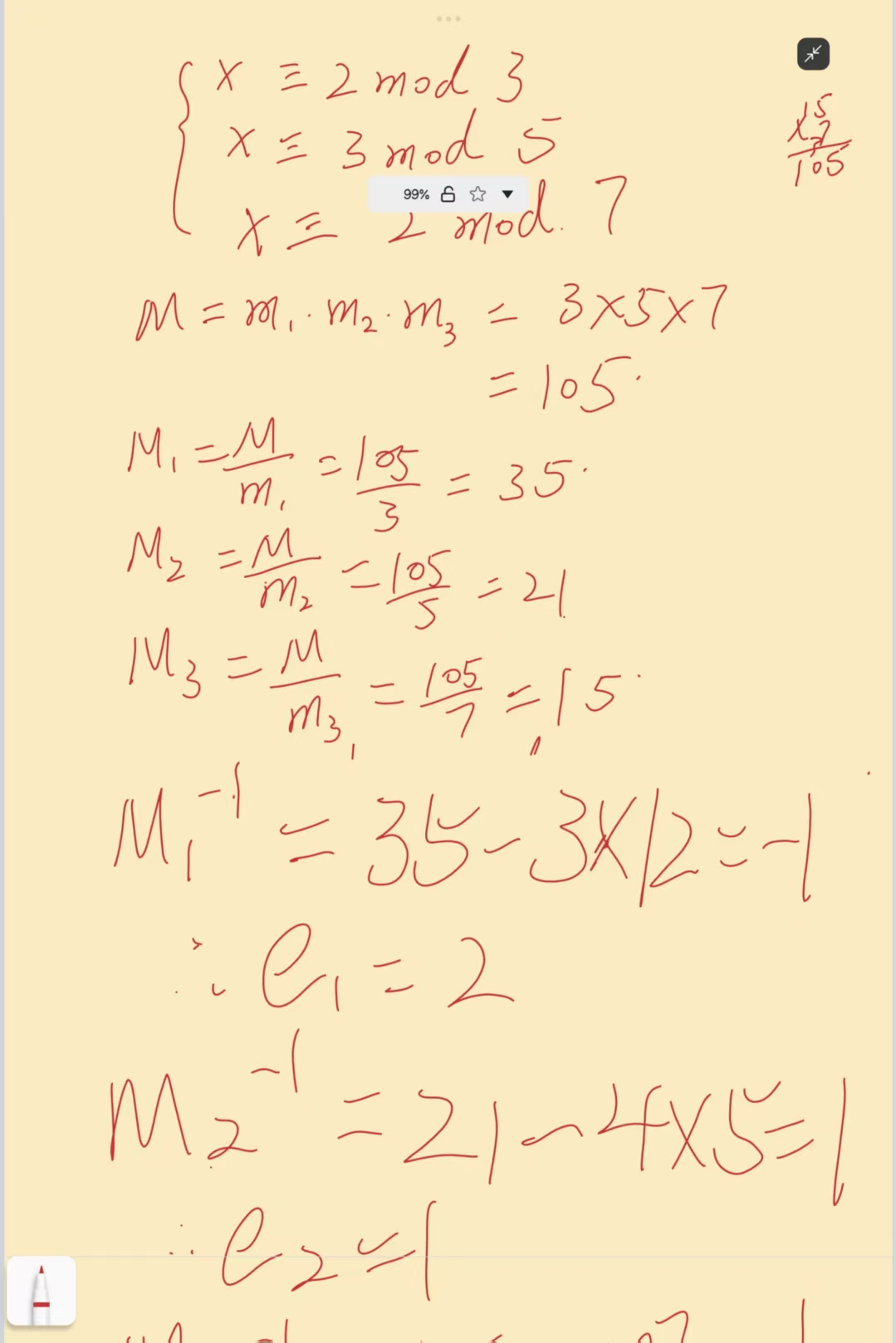
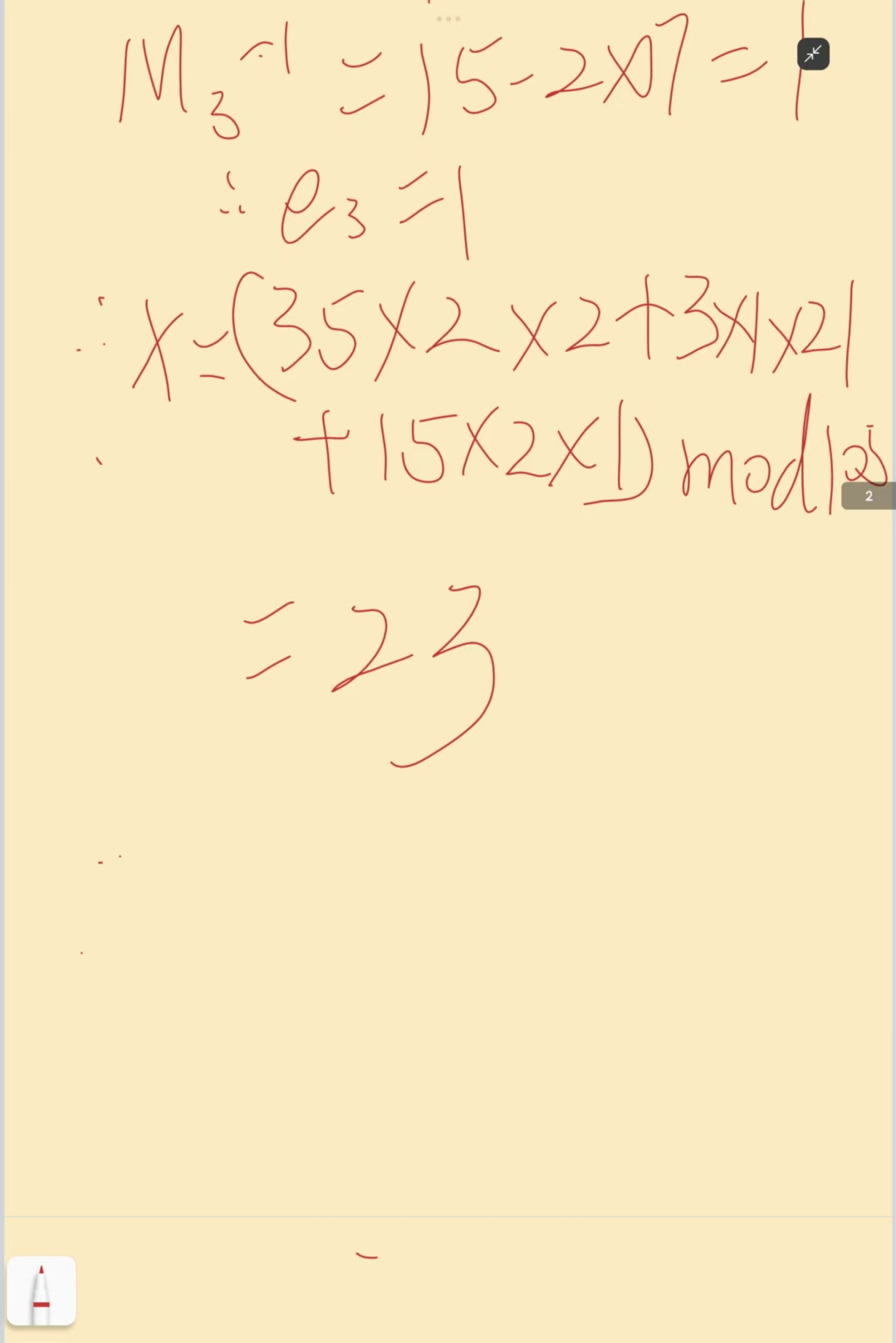
  所以对于中国剩余定理，我们可以写出如下算法步骤：
  判断正整数m1，m2，…，mk是否两两互素，是，则继续；否则跳出；
  计算m = m1m2…mk，Mj = m / mj；
  计算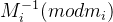
  计算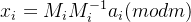
  计算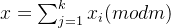

点击查看代码

def extended_gcd(a, b):
    if b == 0:
        return (a, 1, 0)
    else:
        g, x, y = extended_gcd(b, a % b)
        return (g, y, x - (a // b) * y)
 
def crt(remainders, moduli):
    if len(remainders) != len(moduli):
        return None  # 余数和模数数量必须相等
 
    x = 0
    M = 1  # 所有模数的乘积
 
    # 步骤 1: 计算所有模数的乘积 M
    for m in moduli:
        M *= m
 
    # 步骤 2: 循环求解每一个同余方程，并累加结果
    for a_i, m_i in zip(remainders, moduli):
        # 计算 M_i = M / m_i
        M_i = M // m_i
 
        # 步骤 3: 使用扩展欧几里得算法求 M_i 模 m_i 的逆元 inv_i
        # 即求解方程: M_i * inv_i ≡ 1 (mod m_i)
        g, inv_i, _ = extended_gcd(M_i, m_i)
 
        if g != 1:
            # 如果 M_i 和 m_i 的最大公约数不为1，说明模数之间不互质，
            # 在这种情况下，方程组可能无解。
            # 更严谨的做法是检查 a_i % g 是否等于 a_j % g，此处简化处理。
            return None
 
        # 关键步骤：确保逆元是正数
        inv_i = inv_i % m_i
 
        # 步骤 4: 将当前方程的解累加
        # 解的形式为: a_i * M_i * inv_i
        x += a_i * M_i * inv_i
 
    # 步骤 5: 返回最小非负整数解
    return x % M    

1.6 费马小定理

如果p是一个质数，而整数a不是p的倍数，则有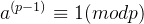
例如：计算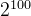除以13的余数

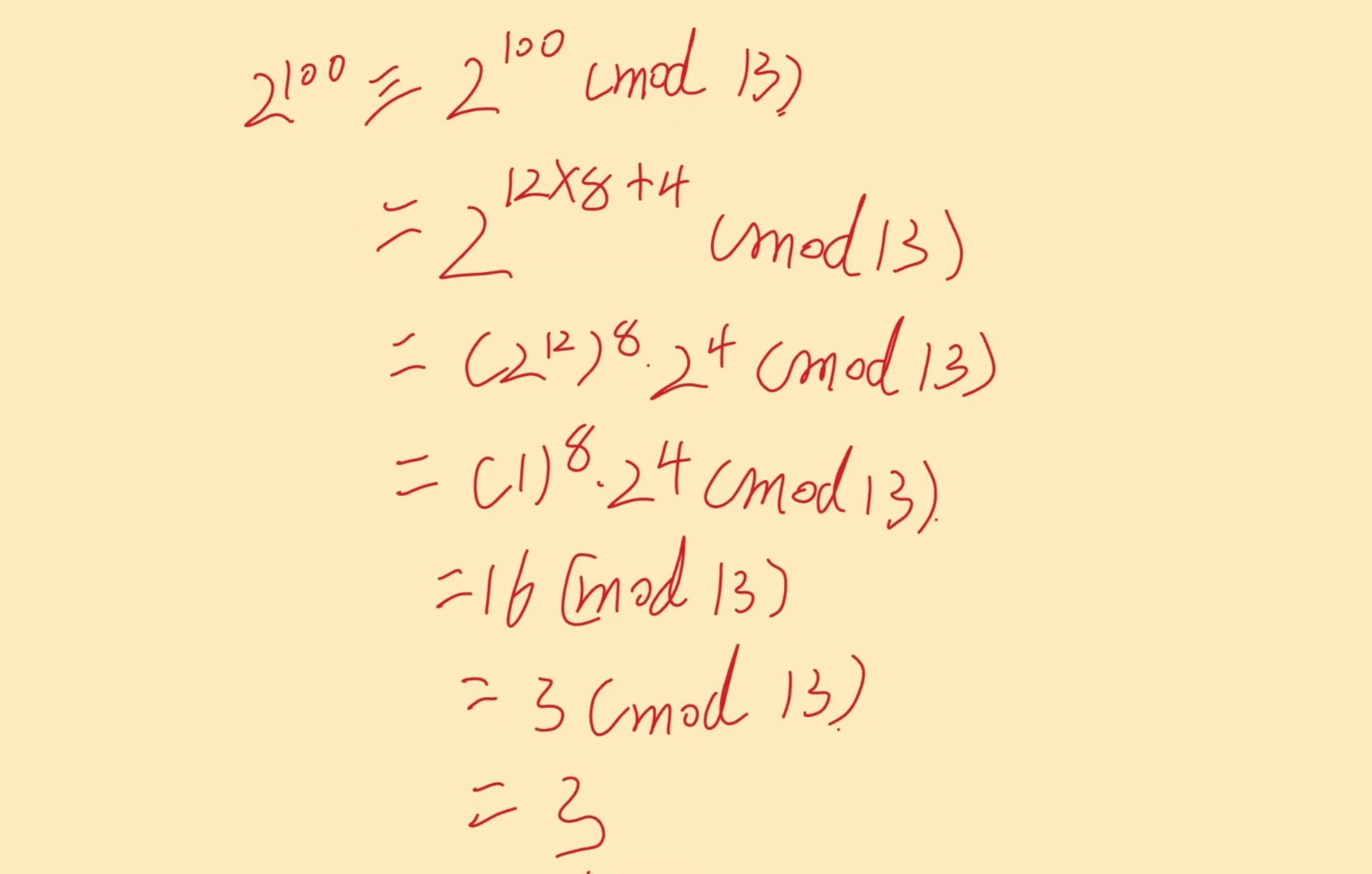
二、仿射密码

仿射密码将字母表中每个字母对应的值使用一个简单的数学函数映射到对应的数值，再把数值转化为字母。同理因为是一个单射函数，所以它也是单表替换加密。
字母和数值对应关系为A、B、C、……、X、Y、Z对应0、1、2、……、23、24、25。
假设我们选择的函数为

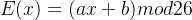
则对应的解密函数为

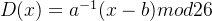
这里的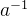即a在模26意义下的逆元。
用代码实现：

点击查看代码

#欧几里得算法
def gcd(a,b):
    if a == 0:
        return b,0,1
    else:
        gcd1,x,y = gcd(b%a,a)
        return gcd1,y - (b//a) * x,x
 
 
#加密
def affine_encrypt(text,a,b):
    result =""
    for char in text:
        if char.isalpha():
            # 计算加密后的字符：(a * (字母的数字表示) + b) % 26
            char_code = (a * (ord(char.upper()) - 65) + b) % 26
            result += chr(char_code + 65)
        else:
            result += char
    return result
 
#解密
def affine_decrypt(text,a,b):
    a_ni = gcd(a,26)[1]
    result =""
    for char in text:
        if char.isalpha():
            # 计算解密后的字符：a的逆元 * (字母的数字表示 - b) % 26
            char_code = (a_ni * ((ord(char.upper()) - 65) - b)) % 26
            result += chr(char_code + 65)
        else:
            result += char
    return result
 
while True:
    print("1.加密")
    print("2.解密")
    print("3.退出")
    choice = input("请输入你的选择：")
    if choice == "1":
        text = input("请输入要加密的文本：")
        a = int(input("请输入a的值："))
        b = int(input("请输入b的值："))
        print("加密后的文本为：" + affine_encrypt(text,a,b))
    elif choice == "2":
        text = input("请输入要解密的文本：")
        a = int(input("请输入a的值："))
        b = int(input("请输入b的值："))
        print("解密后的文本为：" + affine_decrypt(text,a,b))
    elif choice == "3":
        break
    else:
        print("输入错误，请重新输入")