MATLAB-卡尔曼滤波简单运用示例
1、角度和弧度之间的转换公式?
设角度为 angle,弧度为 radian
radian = angle * pi / 180;
angle = radian * 180 / pi;
所以在matlab中经常设置一个参数,用于角度与弧度之间的转换:deg_rad=0.01745329252e0;
2、注意下面角度Angint的表示方法:
Angint=[0,10,0]*deg_rad;
则:Angint(0) = 0;Angint(1) = 0.0175;Angint(2) = 0;
这种表示方法可以在四元数中应用:
例如:
q=[cos(Angint(3)/2)*sin(Angint(2)/2)*cos(Angint(1)/2)+sin(Angint(3)/2)*cos(Angint(2)/2)*sin(Angint(1)/2)
cos(Angint(3)/2)*cos(Angint(2)/2)*sin(Angint(1)/2)-sin(Angint(3)/2)*sin(Angint(2)/2)*cos(Angint(1)/2)
-sin(Angint(3)/2)*cos(Angint(2)/2)*cos(Angint(1)/2)+cos(Angint(3)/2)*sin(Angint(2)/2)*sin(Angint(1)/2)
cos(Angint(3)/2)*cos(Angint(2)/2)*cos(Angint(1)/2)+sin(Angint(3)/2)*sin(Angint(2)/2)*sin(Angint(1)/2)];
可以用q(0)、q(1)、q(2)、q(3)来代入公式计算三轴姿态角。
3、在滤波的过程中,要明确滤波时间和采样频率;
4、IMU数据仿真分析:
(1)先模拟加速度计和陀螺仪的真实输出:
[ Angle,Wibb,Fb ] = imu_true_out( tt,ynong,T );%tt=tt+TT;TT=1/f为时间间隔
注意:加速度计的输出要进行坐标转换: ao=Cnb*([0,0,g]’,
其中:Cnb
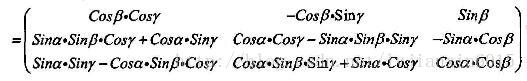
如果你要在加速度计的输出上添加一个随机干扰(可模拟非重力加速度干扰),可以使用函数awgn(); %Add white Gaussian noise to a signal.
ao=Cnb*([0,0,g]’+[0,awgn(0,ynong),0]’); %如果在指点的时间内添加这种干扰,可以加一个if函数
(2)模拟加速度计和陀螺仪的误差:
[Gyro_b,Gyro_r,Gyro_wg,Acc_r]=imu_err_random(tt,TT,Gyro_b,Gyro_r,Gyro_wg,Acc_r);
function [Gyro_b,Gyro_r,Gyro_wg,Acc_r]=imu_err_random(t,T,Gyro_b,Gyro_r,Gyro_wg,Acc_r) g=9.7803698; %重力加速度 (单位:米/秒/秒) Wie=7.292115147e-5; %地球自转角速度(单位:弧度/秒) deg_rad=0.01745329252e0;% Transfer from angle degree to rad Da_bias=[0.001; 0.001; 0.001]*g; %加速度零偏(应与非随机性误差中的加速度零偏保持一致) Ta=1800.0; %加速度一阶马尔可夫过程相关时间 Tg=3600.0; %陀螺一阶马尔可夫过程相关时间 %%%%%%%%%%%%%%%%%%随机性误差%%%%%%%%%%%%%%% if( t==0 ) Acc_r=Da_bias.*randn(3,1); %加速度一阶马尔可夫过程1.0e-4g Gyro_b=0.01*deg_rad/3600.0*randn(3,1); %随机常数0.1(deg/h) Gyro_r=0.01*deg_rad/3600.0*randn(3,1); %陀螺一阶马尔可夫过程0.1(deg/h) Gyro_wg=0.01*deg_rad/3600.0*randn(3,1);%陀螺白噪声0.1(deg/h) else Acc_wa=sqrt(2*T/Ta)*Da_bias.*randn(3,1);%加速度一阶马尔可夫过程白噪声 Acc_r=exp(-1.0*T/Ta)*Acc_r; %加速度一阶马尔可夫过程 Gyro_wr=0.01*sqrt(2*T/Tg)*deg_rad/3600.0*randn(3,1);%陀螺一阶马尔可夫过程白噪声0.1(deg/h) Gyro_r=exp(-1.0*T/Tg)*Gyro_r+Gyro_wr;%陀螺一阶马尔可夫过程0.1(deg/h) Gyro_wg=0.01*deg_rad/3600.0*randn(3,1);%陀螺白噪声0.1(deg/h) end
然后再在while(1)中将真实值+误差值按时间序列存储在数组中以备用,如下:
while tt<=T; [ Angle,Wibb,Fb ] = imu_true_out( tt,ynong,T ); [Gyro_b,Gyro_r,Gyro_wg,Acc_r]=imu_err_random(tt,TT,Gyro_b,Gyro_r,Gyro_wg,Acc_r); Ture_Angle(:,kk)=Angle/deg_rad;%模拟输出的三轴姿态角 gyro(:,kk)=Wibb+Gyro_b+Gyro_r+Gyro_wg;%模拟输出的陀螺仪输出 acc(:,kk)=Fb+Acc_r;%模拟输出的加速度计输出 tt=tt+TT; kk=kk+1;%这里TT=1/f=1/100为采样时间间隔,f为采样频率,T为采样时间,文中设置为30s end
5、函数randn的意思:
R = randn(3,1);%产生3行1列的随机R矩阵,R矩阵满足方差为1,均值为0;注意这里不是说这三个数的方差为1,均值为0,而是每次运行randn时,当运行的量足够大时,所有的R(0)的方差为1,均值为0,R(1)、R(2)同理。
例如1. randn(1) ;%生成一个随机数,要想满足方差为1,均值为0,也必须运行足够多的次数
例如2. x = .6 + sqrt(0.1) * randn(1);%产生均值为0.6,方差为0.1的一个5*5的随机数;sqrt(0.1)对0.1进行开方,直接写0.1那这里就是表示标准差了
randi([m,n],a,b) %[m,n] 的 a*b 随机数
6、axis()函数的用法:
axis([xmin xmax ymin ymax]);%定义x轴和y轴之间的间距
7、set()函数的用法:
plot(t,acc(2,:),'linewidth',1.3); set(gcf,'Position',[100 100 400 300]); %这里的100是指生成的图片距离左下角的距离,400和300分别表示长和宽 axis([0 T -4.9 2.0]); set(gca, 'YTick', [-4.9 -2.4 -0.1 2.0]) set(gca,'fontname','宋体','fontsize',10); %用于改变坐标轴坐标大小,10代表坐标大小; xlabel('时间/s','fontname','宋体','fontsize',10);%用于改变x轴标注的文字和大小; ylabel('加速度计数据/(g)','fontname','宋体','fontsize',10);%用于改变y轴标注的文字和大小; legend('accy');%标注
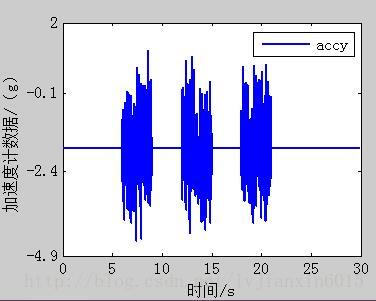
8、EKF的matlab实现:
kalman的前提条件:
1)线性系统
2)系统噪声和测量噪声服从高斯分布
卡尔曼最初提出的滤波理论只适用于线性系统,Bucy,Sunahara等人提出并研究了扩展卡尔曼滤波(Extended Kalman Filter,简称EKF),将卡尔曼滤波理论进一步应用到非线性领域。EKF的基本思想是将非线性系统线性化,然后进行卡尔曼滤波,因此EKF是一种次优滤波。其后,多种二阶广义卡尔曼滤波方法的提出及应用进一步提高了卡尔曼滤波对非线性系统的估计性能。二阶滤波方法考虑了Taylor级数展开的二次项,因此减少了由于 线性化所引起的 估计误差,但大大增加了运算量,因此在实际中反而没有一阶EKF应用广泛。
在状态方程或测量方程为非线性时,通常采用扩展卡尔曼滤波(EKF)。EKF对非线性函数的Taylor展开式进行一阶线性化截断,忽略其余高阶项,从而将非线性问题转化为线性,可以将卡尔曼线性滤波算法应用于非线性系统中。这样一来,解决了非线性问题。EKF虽然应用于非线性状态估计系统中已经得到了学术界认可并为人广泛使用,然而该种方法也带来了两个缺点,其一是当强非线性时EKF违背局部线性假设,Taylor展开式中被忽略的高阶项带来大的 误差时,EKF算法可能会使滤波发散;另外,由于EKF在线性化处理时需要用雅克比(Jacobian)矩阵,其繁琐的计算过程导致该方法实现相对困难。所以,在满足 线性系统、高斯白噪声、所有随机变量服从高斯(Gaussian)分布这3个假设条件时,EKF是最小方差准则下的次优滤波器,其性能依赖于局部非线性度。
%---------------------------EKF算法实现------------------------------------ for k=2:kk-1 %---------------不考虑噪声时,根据状态方程预测当前值-------------------------- Ag=AntiMatrix(gyro(:,k-1));%计算陀螺仪输出的反对称矩阵 Ag=[-Ag, gyro(:,k-1) -gyro(:,k-1)', 0]; Ag=expm(Ag/2/f); %系统一步转移矩阵 Tg=AntiMatrix(q(1:3,k-1)); Tg=[Tg+eye(3)*q(4,k-1) -(q(1:3,k-1))']; Tg=-0.5*Tg/f; %计算系统噪声矩阵 q(:,k)=Ag*q(:,k-1);%计算姿态四元数的状态估计值 %------------------------计算此时的方差------------------------------------- p=Ag*p*Ag'+Tg*Q*Tg'; %------------------------计算卡尔曼增益------------------------------------- r=[0,0,g]'; qv=q(1:3,k); %状态方程四元数矢量部分 qs=q(4,k); %状态方程四元数标量部分 %计算量测向量 Hg=2*[qv'*r*eye(3)+qv*r'-r*qv'+qs*AntiMatrix(r),qs*r+AntiMatrix(r)*qv]; Kg=p*Hg'*(Hg*p*Hg'+R)^-1;%计算卡尔曼增益 %------------------根据当前量测值,对预测更新-------------------------------- Cnb=(qs^2-qv'*qv)*eye(3)+2*qv*qv'-2*qs*AntiMatrix(qv); h=Cnb*r; q(:,k)=q(:,k)+Kg*(acc(:,k)-h); %-----------------------更新估计值方差-------------------------------------- p=(eye(4)-Kg*Hg)*p; %---------------------------归一化----------------------------------------- h(k)=sqrt(q(1,k)^2+q(2,k)^2+q(3,k)^2+q(4,k)^2); q(:,k)=q(:,k)/h(k); %----------------------------姿态角计算------------------------------------- %补偿后(-180,180)180会出现奇点,-180度正常,但是不影响,实际上-180和180是重合的 T33=(q(3,k))^2-(q(2,k))^2-(q(1,k))^2+(q(4,k))^2; T13=2*(q(1,k)*q(3,k)-q(4,k)*q(2,k)); T23=2*(q(2,k)*q(3,k)+q(4,k)*q(1,k)); if T33>0 %根据物理意义不可能出现0 ANGLE0(1,k)=-180/pi*atan(T13/T33); else ANGLE0(1,k)=180/pi*(-pi*sign(T13)-atan(T13/T33)); end ANGLE0(2,k)=180/pi*asin(T23); %俯仰角,绕X轴转动 end
注意此程序的特点,需关注以下问题:
1)如何根据陀螺仪输出计算系统一步转移矩阵:
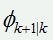
2)如何根据四元数计算系统的噪声矩阵:;
四元数卡尔曼滤波算法的状态方程(由陀螺仪输出计算得到):
;
四元数卡尔曼滤波的时间输出过程如下:
3)如何根据四元数计算系统的量测向量;
Hg=2*[qv’*r*eye(3)+qv*r’-r*qv’+qs*AntiMatrix(r),qs*r+AntiMatrix(r)*qv];
4)如何根据四元数计算系统的转态转移矩阵;
Cnb=(qs^2-qv’*qv)*eye(3)+2*qv*qv’-2*qs*AntiMatrix(qv);
注意对预测值(即四元数)的更新过程:
q(:,k)=q(:,k)+Kg*(acc(:,k)-h);
因为是由加速度计构建系统的量测方程的,acc(:,k)表示加速度计的量测值,h=Cnb*r为先验估计(不考虑误差,r=[0,0,g]’;),这里是将地理坐标系转化为导航坐标系。
实际上,kalman的5个公式一部分是从状态方程和量测方程上获取的。
5)如何根据四元数计算系统的姿态角: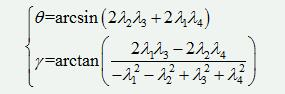
6)反对称矩阵用函数表示AntiMatrix():
function [A] = AntiMatrix(B) A=[0,-B(3,1),B(2,1) B(3,1),0,-B(1,1) -B(2,1),B(1,1),0]; end
----------------------------------------------------------------------分割线----------------------------------------------------------------------------
Z=(1:100); %观测值 noise=randn(1,100); %方差为1的高斯噪声 Z=Z+noise; X=[0; 0]; %状态 Sigma = [1 0; 0 1]; %状态协方差矩阵 F=[1 1; 0 1]; %状态转移矩阵 Q=[0.0001, 0; 0 0.0001]; %状态转移协方差矩阵 H=[1 0]; %观测矩阵 R=1; %观测噪声方差 figure; hold on; for i=1:100 X_ = F*X; Sigma_ = F*Sigma*F'+Q; K = Sigma_*H'/(H*Sigma_*H'+R); X = X_+K*(Z(i)-H*X_); Sigma = (eye(2)-K*H)*Sigma_; plot(X(1), X(2), '.','MarkerSize',10); %画点,横轴表示位置,纵轴表示速度 end plot([0,100],[1,1],'r-');
----------------------------------------------------------------------分割线----------------------------------------------------------------------------
一.离散时间线性动态系统的状态方程
线性系统采用状态方程、观测方程及其初始条件来描述。线性离散时间系统的一般状态方程可描述为
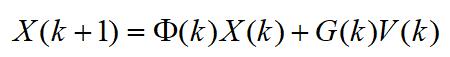
其中,X(k) 是 k 时刻目标的状态向量,V(k)是过程噪声,它是具有均值为零、方差矩阵为 Q(k) 的高斯噪声向量,即
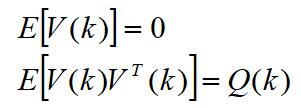
Q(k)是状态转移矩阵, G(k)是过程噪声增益矩阵。
二.传感器的测量(观测)方程
传感器的通用观测方程为
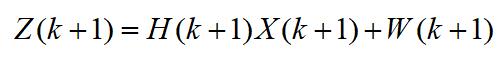
这里, Z(k+1)是传感器在 k+1 时刻的观测向量,观测噪声 W(k+1) 是具有零均值和正定协方差矩阵 R(k+1) 的高斯分布测量噪声向量,即
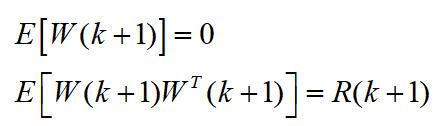
三.初始状态的描述
初始状态 X(0) 是高斯的,具有均值 X(0|0) 和协方差 ,即
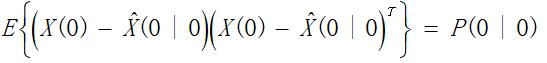
四.Kalman滤波算法
状态估计的一步预测方程为
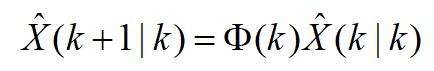
一步预测的协方差为
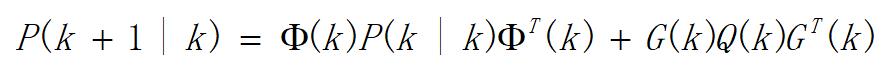
预测的观测向量为
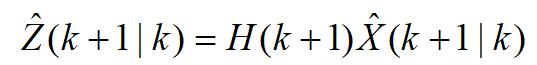
观测向量的预测误差协方差为
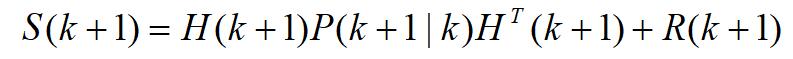
新息或量测残差为
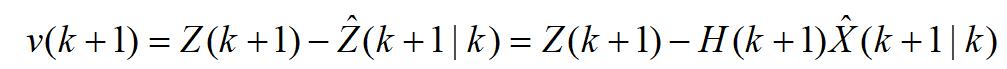
滤波器增益为
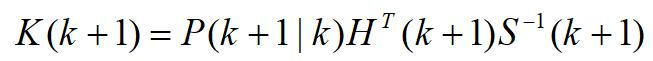
Kalman滤波算法的状态更新方程为
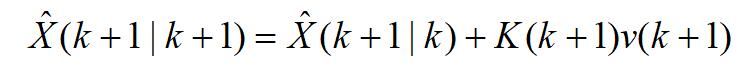
滤波误差协方差的更新方程为
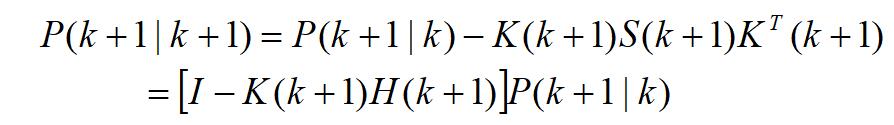
% Kalman滤波技术 A=1; % 状态转移矩阵 Φ(k) H=0.2; % 观测矩阵 H(k) X(1)=0; % 目标的状态向量 X(k) % V(1)=0; % 过程噪声 V(k) Y(1)=1; % 一步预测x(k)的更新 X(k+1|k+1) P(1)=10; % 一步预测的协方差 P(k) N=200; V=randn(1,N); % 模拟产生过程噪声(高斯分布的随机噪声) w=randn(1,N); % 模拟产生测量噪声 for k=2:N X(k) = A * X(k-1)+V(k-1); % 状态方程:X(k+1)=Φ(k)X(k)+G(k)V(k),其中G(k)=1 end Q=std(V)^2; % W(k)的协方差,std()函数用于计算标准偏差 R=std(w)^2; % V(k)的协方差 covariance Z=H*X+w; % 观测方程:Z(k+1)=H(k+1)X(k+1)+W(k+1),Z(k+1)是k+1时刻的观测值 for t=2:N P(t) = A * P(t-1)+Q; % 一步预测的协方差 P(k+1|k) S(t) = H.^2 * P(t)+R; % 观测向量的预测误差协方差 S(k+1) K(t) = H * P(t)/S(t); % 卡尔曼滤波器增益 K(k+1) v(t) = Z(t) - ( A * H * Y(t-1) ); % 新息/量测残差 v(k+1) Y(t)=A * Y(t-1) + K(t) * v(t); % 状态更新方程 X(k+1|k+1)=X(k+1|k)+K(k+1)*v(k+1) P(t)=(1-H * K(t)) * P(t); % 误差协方差的更新方程: P(k+1|k+1)=(I-K(k+1)*H(k+1))*P(k+1|k) end t=1:N; plot(t,Y,'r',t,Z,'g',t,X,'b'); % 红色线最优化估算结果滤波后的值,%绿色线观测值,蓝色线预测值 legend('Kalman滤波结果','观测值','预测值');
----------------------------------------------------------------------分割线----------------------------------------------------------------------------
但在实际工作中,我们的系统几乎都是非线性的,所以如何解决非线性系统 的滤波问题呢,这就是我们要讲的EKF(扩展卡尔曼滤波),它的原理很简单,就是在估计状态的地方进行线性化,线性化的方法也很简单,只需要进行泰勒的一 阶展开就行。当然我们也要说一下缺点,因为我们选择的线性化方法,所以只能达到二阶的精度(UKF可以达到四阶的精度),所以要求我们的系统是弱线性化 的。其实UKF也是对非线性系统的卡尔曼滤波,主要本人对其线性化方法(UT变换)不是很理解,等考完试再说。
首先,系统的状态方程和观测方程如下:
我们知道,在更新误差协方差矩阵的时候,不能直接用f和h的,所以我们要进行泰勒展开,也就是要求雅克比矩阵。再利用线性情况下的卡尔曼滤波进行计算更新。
预测:
利用雅克比矩阵进行更新模型:
更新:
下面我会展示一个目标追踪的EKF例子:
%扩展Kalman滤波在目标跟踪中的应用 %function EKF_For_TargetTracking clc;clear; T=1;%雷达扫描周期 N=60/T;%总的采样次数 X=zeros(4,N);%目标真实位置、速度 X(:,1)=[-100,2,200,20];%目标初始位置、速度 Z=zeros(1,N);%传感器对位置的观测 delta_w=1e-3;%如果增大这个参数,目标的真实轨迹就是曲线了 Q=delta_w*diag([0.5,1]);%过程噪声方差 G=[T^2/2,0;T,0;0,T^2/2;0,T];%过程噪声驱动矩阵 R=5;%观测噪声方差 F=[1,T,0,0;0,1,0,0;0,0,1,T;0,0,0,1];%状态转移矩阵 x0=200;%观测站的位置 y0=300; Xstation=[x0,y0]; for t=2:N X(:,t)=F*X(:,t-1)+G*sqrtm(Q)*randn(2,1);%目标真实轨迹 end for t=1:N Z(t)=Dist(X(:,t),Xstation)+sqrtm(R)*randn;%观测值 end %EKF Xekf=zeros(4,N); Xekf(:,1)=X(:,1);%Kalman滤波的状态初始化 P0=eye(4);%误差协方差矩阵的初始化 for i=2:N Xn=F*Xekf(:,i-1);%一步预测 P1=F*P0*F'+G*Q*G';%预测误差协方差 dd=Dist(Xn,Xstation);%观测预测 %求解雅克比矩阵H H=[(Xn(1,1)-x0)/dd,0,(Xn(3,1)-y0)/dd,0];%泰勒展开的一阶近似 K=P1*H'*inv(H*P1*H'+R);%卡尔曼最优增益 Xekf(:,i)=Xn+K*(Z(:,i)-dd);%状态更新 P0=(eye(4)-K*H)*P1;%滤波误差协方差更新 end %误差分析 for i=1:N Err_KalmanFilter(i)=Dist(X(:,i),Xekf(:,i));% end %画图 figure hold on;box on; plot(X(1,:),X(3,:),'-k');%真实轨迹 plot(Xekf(1,:),Xekf(3,:),'-r');%扩展Kalman滤波轨迹 legend(' real trajectory','EKF trajectory'); xlabel('X-axis X/m'); ylabel('Y-axis Y/m'); figure hold on ;box on; plot(Err_KalmanFilter,'-ks','MarkerFace','r') xlabel('Time /s'); ylabel('Position estimation bias /m'); %子函数 求欧氏距离 function d=Dist(X1,X2); if length(X2)<=2 d=sqrt((X1(1)-X2(1))^2+(X1(3)-X2(2))^2); else d=sqrt((X1(1)-X2(1))^2+(X1(3)-X2(3))^2); end %子函数 求欧氏距离 function d=Dist(X1,X2); if length(X2)<=2 d=sqrt((X1(1)-X2(1))^2+(X1(3)-X2(2))^2); else d=sqrt((X1(1)-X2(1))^2+(X1(3)-X2(3))^2); end



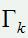 ;
;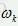 输出计算得到):
输出计算得到): 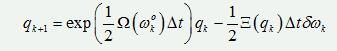 ;
;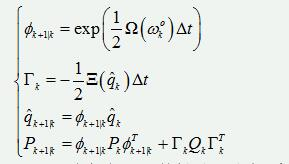













 浙公网安备 33010602011771号
浙公网安备 33010602011771号