Quoit Design

以下为本题用到的算法

概述

给定 \(n\) 个二维平面上的点，求一组欧几里得距离最近的点对。

下面我们介绍一种时间复杂度为 \(O(n\log n)\) 的分治算法来解决这个问题。该算法在 1975 年由 Franco P. Preparata 提出，Preparata 和 Michael Ian Shamos 证明了该算法在决策树模型下是最优的。

算法

与常规的分治算法一样，我们将这个有 \(n\) 个点的集合拆分成两个大小相同的集合 \(S_1, S_2\)，并不断递归下去。但是我们遇到了一个难题：如何合并？即如何求出一个点在 \(S_1\) 中，另一个点在 \(S_2\) 中的最近点对？这里我们先假设合并操作的时间复杂度为 \(O(n)\)，可知算法总复杂度为 \(T(n) = 2T(\frac{n}{2}) + O(n) = O(n\log n)\)。

我们先将所有点按照 \(x_i\) 为第一关键字、\(y_i\) 为第二关键字排序，并以点 \(p_m (m = \lfloor \frac{n}{2} \rfloor)\) 为分界点，拆分点集为 \(A_1,A_2\)：

\[A_1 = \{p_i \ \big | \ i = 0 \ldots m \}\\ A_2 = \{p_i \ \big | \ i = m + 1 \ldots n-1 \} \]

并递归下去，求出两点集各自内部的最近点对，设距离为 \(h_1,h_2\)，取较小值设为 \(h\)。

现在该合并了！我们试图找到这样的一组点对，其中一个属于 \(A_1\)，另一个属于 \(A_2\)，且二者距离小于 \(h\)。因此我们将所有横坐标与 \(x_m\) 的差小于 \(h\) 的点放入集合 \(B\)：

\[B = \{ p_i \ \big | \ \lvert x_i - x_m \rvert < h \} \]

结合图像，直线 \(m\) 将点分成了两部分。\(m\) 左侧为 \(A_1\) 点集，右侧为为 \(A_2\) 点集。

再根据 \(B = \{ p_i \ \big | \ \lvert x_i - x_m \rvert < h \}\) 规则，得到绿色点组成的 \(B\) 点集。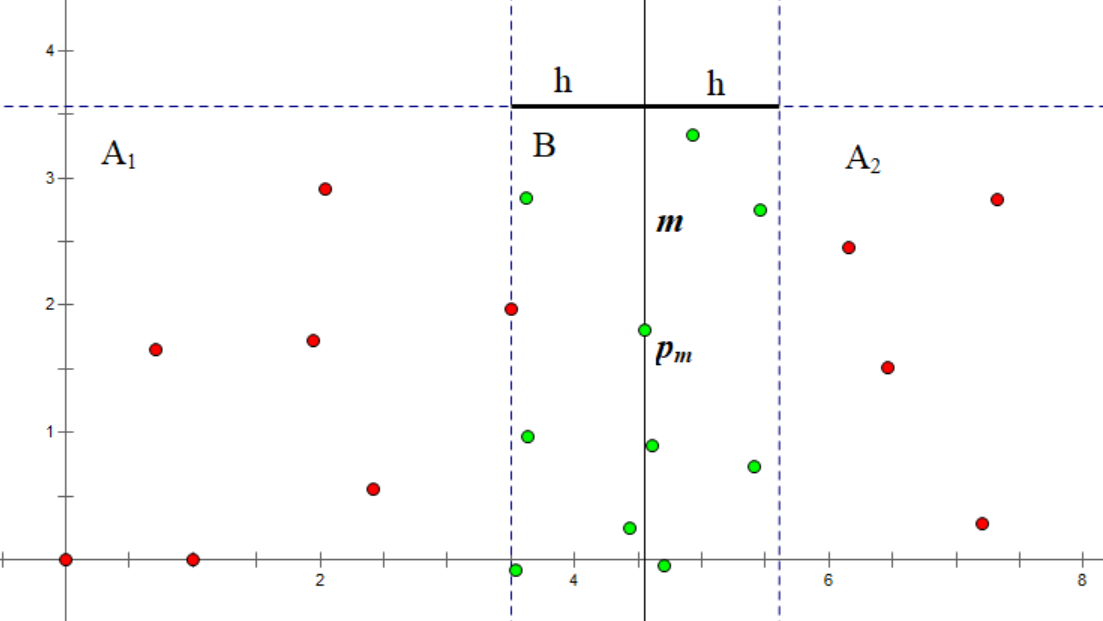

对于 \(B\) 中的每个点 \(p_i\)，我们当前目标是找到一个同样在 \(B\) 中、且到其距离小于 \(h\) 的点。为了避免两个点之间互相考虑，我们只考虑那些纵坐标小于 \(y_i\) 的点。显然对于一个合法的点 \(p_j\)，\(y_i - y_j\) 必须小于 \(h\)。于是我们获得了一个集合 \(C(p_i)\)：

\[C(p_i) = \{ p_j\ \big |\ p_j \in B,\ y_i - h < y_j \le y_i \} \]

在点集 \(B\) 中选一点 \(p_i\)，根据 \(C(p_i) = \{ p_j\ \big |\ p_j \in B,\ y_i - h < y_j \le y_i \}\) 的规则，得到了由红色方框内的黄色点组成的 \(C\) 点集。

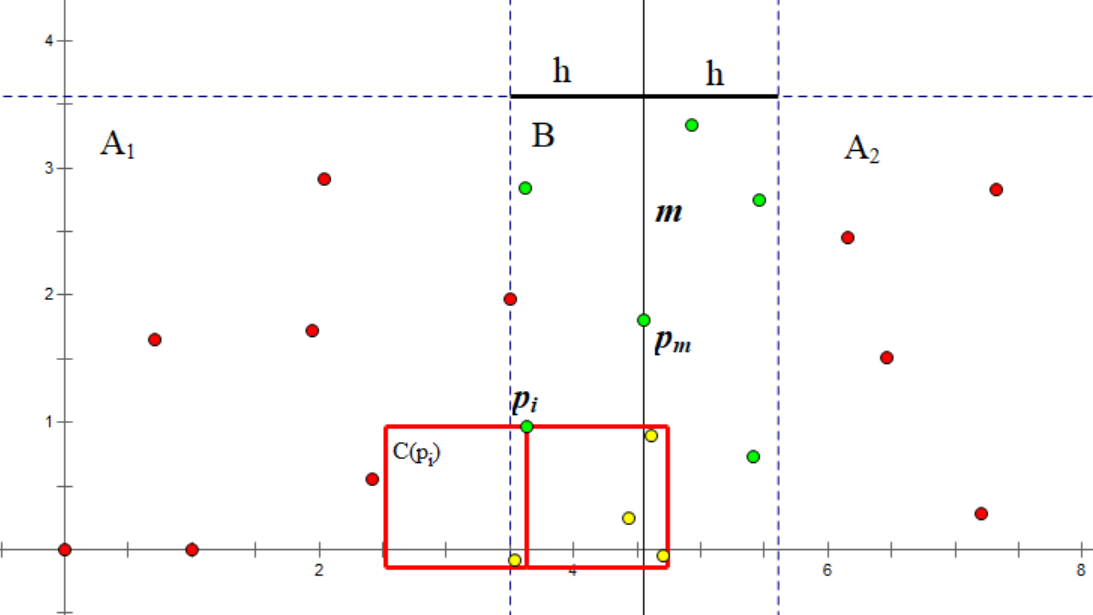
如果我们将 \(B\) 中的点按照 \(y_i\) 排序，\(C(p_i)\) 将很容易得到，即紧邻 \(p_i\) 的连续几个点。

由此我们得到了合并的步骤：

1. 构建集合 \(B\)。
2. 将 \(B\) 中的点按照 \(y_i\) 排序。通常做法是 \(O(n\log n)\)，但是我们可以改变策略优化到 \(O(n)\)（下文讲解）。
3. 对于每个 \(p_i \in B\) 考虑 \(p_j \in C(p_i)\)，对于每对 \((p_i,p_j)\) 计算距离并更新答案（当前所处集合的最近点对）。

注意到我们上文提到了两次排序，因为点坐标全程不变，第一次排序可以只在分治开始前进行一次。我们令每次递归返回当前点集按 \(y_i\) 排序的结果，对于第二次排序，上层直接使用下层的两个分别排序过的点集归并即可。

似乎这个算法仍然不优，\(|C(p_i)|\) 将处于 \(O(n)\) 数量级，导致总复杂度不对。其实不然，其最大大小为 \(7\)，我们给出它的证明：

复杂度证明

我们已经了解到，\(C(p_i)\) 中的所有点的纵坐标都在 \((y_i-h,y_i]\) 范围内；且 \(C(p_i)\) 中的所有点，和 \(p_i\) 本身，横坐标都在 \((x_m-h,x_m+h)\) 范围内。这构成了一个 \(2h \times h\) 的矩形。

我们再将这个矩形拆分为两个 \(h \times h\) 的正方形，不考虑 \(p_i\)，其中一个正方形中的点为 \(C(p_i) \cap A_1\)，另一个为 \(C(p_i) \cap A_2\)，且两个正方形内的任意两点间距离大于 \(h\)。（因为它们来自同一下层递归）

我们将一个 \(h \times h\) 的正方形拆分为四个 \(\frac{h}{2} \times \frac{h}{2}\) 的小正方形。可以发现，每个小正方形中最多有 \(1\) 个点：因为该小正方形中任意两点最大距离是对角线的长度，即 \(\frac{h}{\sqrt 2}\)，该数小于 \(h\)。

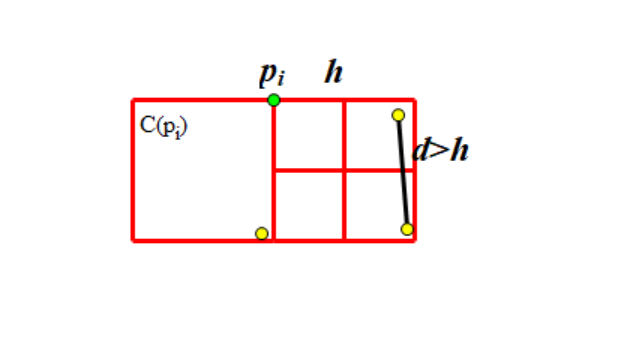
由此，每个正方形中最多有 \(4\) 个点，矩形中最多有 \(8\) 个点，去掉 \(p_i\) 本身，\(\max(C(p_i))=7\)。

#include<bits/stdc++.h>
using namespace std;

struct point
{
    double x,y;
    int id;
};

vector<point>a,t;
double midsdis;
int ansa,ansb;

bool cmp_x(const point &a,const point &b)
{
    return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
bool cmp_y(const point &a,const point &b)
{
    return a.y<b.y;//不关注x坐标
}

void up_ans(const point &a,const point &b)//更新答案
{
    //点对的距离
    double dis=sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
    if(dis<midsdis)
        midsdis=dis,ansa=a.id,ansb=b.id;//ans与id是更新点对
}

void divi(int l,int r)
{
    //1、先写边界条件
    if(r-l<=3){//此时可以暴力跑出最短点对
        for(int i=l;i<r;i++)
            for(int j=i+1;j<=r;j++)
               up_ans(a[i],a[j]);
        sort(a.begin()+l,a.begin()+r,cmp_y);//!!!
        return;
    }
    //2、 开始分治，去触及最小/边界条件
    int mid=(l+r)>>1;
    int midx=a[mid].x;
    divi(l,mid);
    divi(mid,r);
    //合并答案
    //merge()把两个有序的数列合并，copy（）是把他放回去
    merge(a.begin()+l,a.begin()+mid,a.begin()+mid,a.begin()+r,t.begin(),cmp_y) ;//正常使用5个参数，表示结构体大小，再加一个参数
    copy(t.begin(),t.begin()+r-l,a.begin()+l);

    int tsz=0;
    for(int i=l;i<r;i++){
        if(fabs(a[i].x-midx)<midsdis)//小于中线的位置
        {
            for(int j=tsz-1;j>=0&&a[i].y-t[j].y<midsdis;j--){
                up_ans(a[i],t[j]);
            }
                t[tsz++]=a[i];
        }

    }
}

int main()
{
    int n;
    while(~scanf("%d",&n)&&n!=0)
    {

        if(n==1)
        {
            double xx,yy;
            scanf("%lf %lf",&xx,&yy);
            printf("0\n");
            continue;
        }
        else
        {
            a.clear();
            t.clear();
            for(int i=0;i<n;i++)
            {
                point p;

                double xx,yy;
                scanf("%lf %lf",&xx,&yy);
                p.x=xx;
                p.y=yy;
                p.id=i;
                a.push_back(p);
            }
            sort(a.begin(),a.end(),cmp_x);
            midsdis=1e20;
            t.resize(n);//给t分配n个空间
            divi(0,n-1);
            printf("%.2f\n",midsdis/2.0);
        }

    }
    return 0;
}

本文来自hrbust hzy，侵删。