摘要：
Problem 已知抛物线 $C:~y^2=2x$ 的焦点为 $F$，准线为 $l$，点 $P$ 为抛物线 $C$ 上一动点（异于顶点），过 $P$ 做准线 $l$ 的垂线，垂足为 $H$，且 $\triangle PFH$ 重心为 $M$，求证 $MP$ 与抛物线 $C$相切。 Solution 阅读全文
摘要：
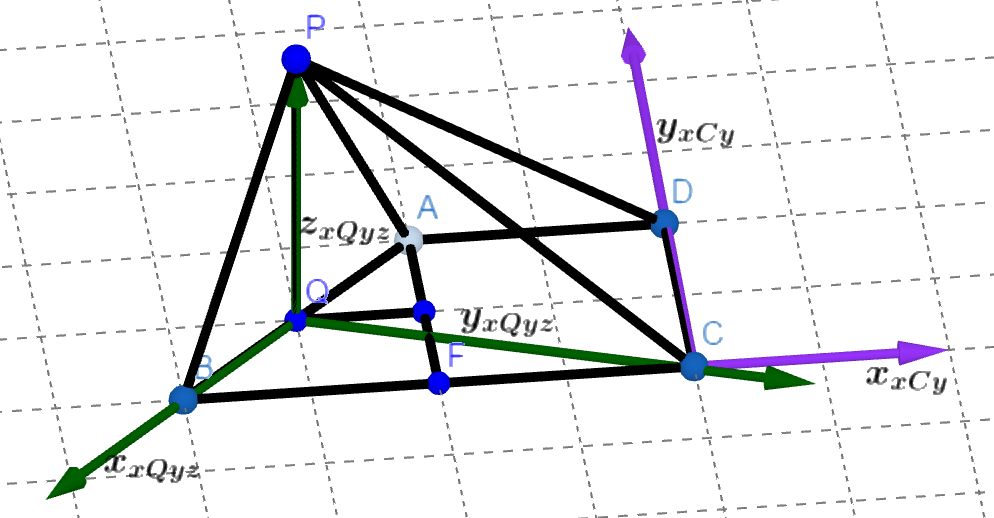如图所示，四边形 $ABCD$ 是直角梯形，$AD\parallel BC$，$AD\bot CD$，$\angle ABC=\frac{\pi}{3}$，$BC=2AD=2$，$PC=3$，$\triangle PAB$ 为等边三角形. 求证 $AB\bot PC$.
阅读全文
如图所示，四边形 $ABCD$ 是直角梯形，$AD\parallel BC$，$AD\bot CD$，$\angle ABC=\frac{\pi}{3}$，$BC=2AD=2$，$PC=3$，$\triangle PAB$ 为等边三角形. 求证 $AB\bot PC$.
阅读全文
摘要：
Forewords 今年 USACO 的比赛变化挺大的，有部分分了，而且不再是固定十个点了（部分分只说这几个点满足这几个性质，以为十个点的我还高兴了一会，一提交，...），除此之外居然赛后还排名了。这场打得意外的顺手，但是还是有点小遗憾吧。样例强度还是有点不够高的，但 IOI 赛制嘛，也不能说啥。 阅读全文
摘要：
这题其实和 "NIKKEI 2019 2 D Shortest Path on a Line" 差不多的啦，都是一种最短路的变形，把多个点和边关联了起来。 "题面" 你要从一楼到 $n$ 楼去，每层楼可以选择坐电梯和走楼梯，第 $i$ 和 $i+1$ 层之间的楼梯花费 $a_i$ 时间，而电梯花费 阅读全文
摘要：
请注意本文章所描写的算法只可以获得前 14 个测试点（含三个样例）的部分分，但是没有出现 WA 的情况。 "推荐阅读" "题面" 给出 $m$ 个线段，每次可以从线段上任意一点以代价 $c_i$ 走到线段上另一点，每条线段只能使用一次，求从 $1$ 位置走到 $n$ 位置的最小代价。 部分分题解 观 阅读全文
摘要：
题面 $q$ 个询问，每个询问给出一个字符串 $s$，要你在 $s$ 中用最小替换得到无穷字符串 的长度为定值 $k$ 的子串。 题解 一眼看过去可能是编辑距离什么的，但是仔细看 Hard 下的时间复杂度不允许，然后进行了一波分析... 上图模式串 2 同理。 从上图可以发现，其实就是主串往后移动一 阅读全文
摘要：
题意 有 $n$ 个数 $s+1\ldots s+n$，求是否能将这 $n$ 个数放到 $1\ldots n$ 上，且当令原数为 $x$，放到 $y$ 位置时有 $x \mod y=0$。 不超过 $100$ 组数据，$1\le n \le 10^9,0\le s\le 10^9$。 题解 看上去很 阅读全文
摘要：
Part A 预处理 预处理有，分析出联通块和文字区域 联通块分析 这个是个很简单的操作，因为之前已经把图像数据读入 vector 中了，但实际操作时有些问题。 一个就是，此处“联通块”的定义和一般定义不同，此处“联通块”的目的是找出各个字符所在区域，因此需要去除包含的联通块情况，如下图所示，上面的 阅读全文
摘要：
foreword ummm... 开始前几个小时被朋友拉来打了这一场，总体海星，题目体验极佳，很符合口味，稍微有点点简单了不知道是不是因为是 New Year Round，很快就打到了 D，但是题目阅读难度有点点大，Alice 和 Bob 永远离不开的博弈论，呼应去年的博弈论。 少有的评测机出锅（也 阅读全文
摘要：
前言 由于计算机最擅长二进制处理，因此将图片导入到计算模块前需要进行颜色空间上的调整，将 RGB 空间调整为黑白二色的颜色空间，同时对图像形态进行简单优化，使得处理更加快捷，处理效果更优化。 颜色空间转换 颜色空间调节的目标是将其从 RGB 空间调节到黑白颜色空间。首先，输入的是一张彩色图片，要将他 阅读全文