比较排序-交换排序(1)-冒泡排序算法

算法介绍

​ 冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

算法描述

• 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
• 针对所有的元素重复以上的步骤，除了最后一个；
• 重复步骤1~3，直到排序完成。

动图演示

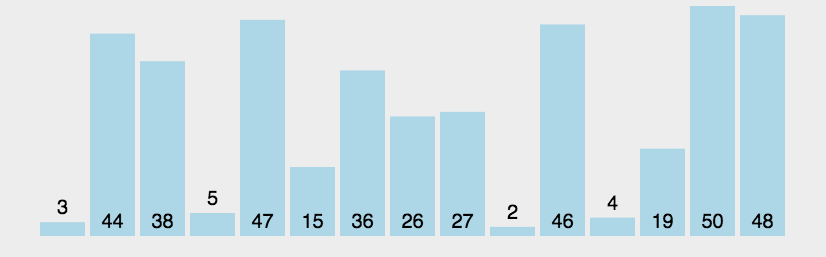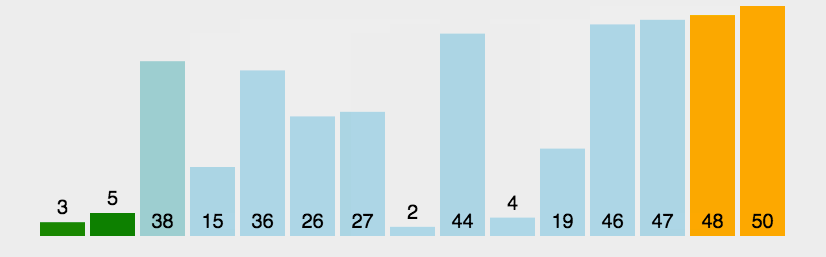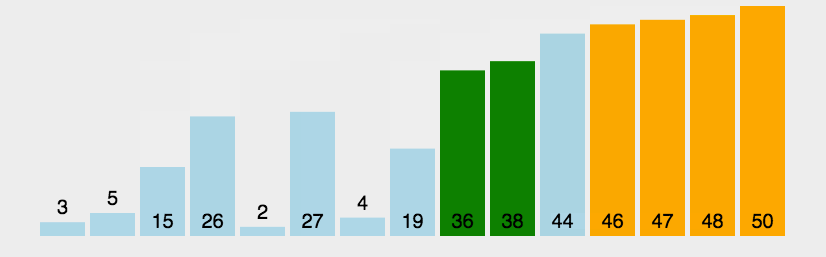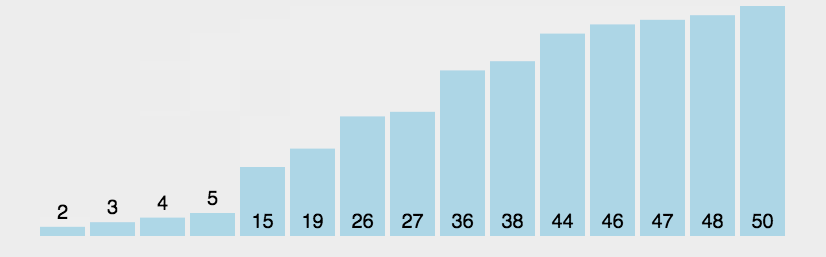
代码实现

第一版：

算法思想：每次都是从头一直比较到尾，即使有些元素已经有序了

func bubbleSort1(toSortNumbers []int) error {
	if len(toSortNumbers) == 0 {
		return fmt.Errorf("the sorting array is empty, nothing to do")
	}
	//最后一个元素不用再排序了，因此循环次数为：len(toSortNumbers)-1 次
	for i := 0; i < len(toSortNumbers)-1; i++ {
		var exchangeCount int
		for j := 0; j < len(toSortNumbers)-1; j++ {
			if toSortNumbers[j] > toSortNumbers[j+1] {
				exchangeCount++
				toSortNumbers[j], toSortNumbers[j+1] = toSortNumbers[j+1], toSortNumbers[j]
			}
		}
		if exchangeCount == 0 {
			break
		}
	}
	return nil
}

第二版

算法思想：外层循环最多只循环 length - 1 次，外层循环执行完一次，就有一个最大元素产生且已排好序，剩下的元素无须再和这些已排序的元素比较。

func bubbleSort2(toSortNumbers []int) error {
	if len(toSortNumbers) == 0 {
		return fmt.Errorf("the sorting array is empty, nothing to do")
	}
	//最后一个元素不用再排序了，因此循环次数为：len(toSortNumbers)-1 次
	for i := 0; i < len(toSortNumbers)-1; i++ {
		//后期优化参数，用于统计外循环执行次数
		outer++
		/*
			外层循环执行完一次，就有一个最大元素产生且已排好序，剩下的元素无须再和这些已排序的元素比较，因此就外层循环的i，
			就代表不用比较的元素个数。下面的len(toSortNumbers)-i-1 的"-1"为了防止数组越界。
		*/
		for j := 0; j < len(toSortNumbers)-i-1; j++ {
			//后期优化参数，用于统计内循环执行次数
			inner++
			if toSortNumbers[j] > toSortNumbers[j+1] {
				exchangeCount++
				toSortNumbers[j], toSortNumbers[j+1] = toSortNumbers[j+1], toSortNumbers[j]
			}
		}
	}
	return nil
}

第三版

算法思想：内层循环只要没有交换，说明当前序列已经有序，直接break掉外层循环，排序完成，这次就大大减少了内外层循环执行次数。

func bubbleSort3(toSortNumbers []int) error {
	if len(toSortNumbers) == 0 {
		return fmt.Errorf("the sorting array is empty, nothing to do")
	}
	//最后一个元素不用再排序了，因此循环次数为：len(toSortNumbers)-1 次
	for i := 0; i < len(toSortNumbers)-1; i++ {
		//后期优化参数，用于统计外循环执行次数
		outer++
		var exchangeCount int
		/*
			循环执行完一次，就有一个最大元素产生且已排好序，剩下的元素无须再和这些已排序的元素比较，因此就外层循环的i，
			就代表不用比较的元素个数。下面的len(toSortNumbers)-i-1 的"-1"为了防止数组越界。
		*/
		for j := 0; j < len(toSortNumbers)-i-1; j++ {
			//后期优化参数，用于统计内循环执行次数
			inner++
			if toSortNumbers[j] > toSortNumbers[j+1] {
				exchangeCount++
				toSortNumbers[j], toSortNumbers[j+1] = toSortNumbers[j+1], toSortNumbers[j]
			}
		}
		if exchangeCount == 0 {
			break
		}
	}
	return nil
}

第二版与第三版比较

func main() {
	/* test case:
	{7, 5, 6, 3, 4, 1, 2}
	{7, 6, 5, 4, 3, 2, 1}
	{1, 3, 5, 1, 8, 2, 0, 4, 6, 7, 5}
	{1, 3, 1, 3, 2, 9, 8, 1, 1, 8, 7}
	{1, 8, 7, 8, 4, 8, 5, 2, 6, 1, 8}
	{1, 2, 3, 4, 5, 6, 7}
	{1, 3, 2, 4, 5, 6, 7}
	*/
	toSort := []int{1, 2, 3, 4, 5, 6, 7}
	fmt.Println("排序前：", toSort)
	_ = bubbleSort2(toSort)
    // _ = bubbleSort3(toSort)
	fmt.Println("排序后：", toSort)
	fmt.Printf("outer: %d, innner: %d", outer, inner)
}

第二版结果：

排序前： [1 2 3 4 5 6 7]
排序后： [1 2 3 4 5 6 7]
outer: 6, innner: 21
Process finished with exit code 0

第三版结果：

排序前： [1 2 3 4 5 6 7]
排序后： [1 2 3 4 5 6 7]
outer: 1, innner: 6
Process finished with exit code 0

小结：第三版的的内外层执行次数明显大于第二版，第三版可以提高算法效率！