NOIP2017 列队
前置技能:动态开点线段树
题意:
Sylvia是一个热爱学习的女♂孩子。前段时间,
Sylvia参加了学校的军训。众所周知,军训的时候需要站方阵。Sylvia 所在的方阵中有 n*m 名学生,方阵的行数为 n ,列数为 m 。
为了便于管理,教官在训练开始时,按照从前到后,从左到右的顺序给方阵中 的学生从 1 到 n*m 编上了号码(参见后面的样例)。即:初始时,第 i 行第 j 列 的学生的编号是 (i−1)*m+j 。
然而在练习方阵的时候,经常会有学生因为各种各样的事情需要离队。在一天 中,一共发生了 qq 件这样的离队事件。每一次离队事件可以用数对 (x,y) (1≤x≤n, 1≤y≤m)(x,y)(1≤x≤n,1≤y≤m) 描述,表示第 x 行第 y 列的学生离队。
在有学生离队后,队伍中出现了一个空位。为了队伍的整齐,教官会依次下达 这样的两条指令:
向左看齐。这时第一列保持不动,所有学生向左填补空缺。不难发现在这条 指令之后,空位在第 x 行第 m 列。
向前看齐。这时第一行保持不动,所有学生向前填补空缺。不难发现在这条 指令之后,空位在第 n 行第 m 列。
教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后, 下一个学生才能离队。因此在每一个离队的学生要归队时,队伍中有且仅有第 n 行 第 m 列一个空位,这时这个学生会自然地填补到这个位置。
因为站方阵真的很无聊,所以
Sylvia想要计算每一次离队事件中,离队的同学 的编号是多少。注意:每一个同学的编号不会随着离队事件的发生而改变,在发生离队事件后 方阵中同学的编号可能是乱序的。
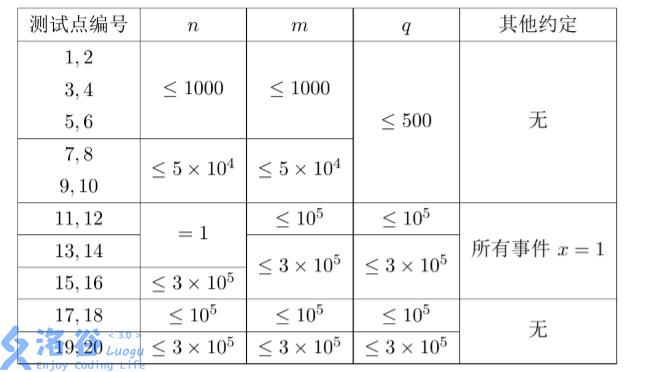
q<=500 50分 模拟
只有500组询问,妥妥的暴力
但是如果开出n*m的数组,空间就会炸
不难发现每个人的出队只会影响当前行和最后一列
所以只要维护这p行和最后一列的信息,空间复杂度:O(p*m+n)
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
#define N 501
#define M 50001
typedef long long LL;
LL pos[N][M],last[M];
struct node
{
int x,y;
}e[N];
int h[N];
void read(int &x)
{
x=0; char c=getchar();
while(!isdigit(c)) c=getchar();
while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); }
}
int main()
{
int n,m,q;
read(n); read(m); read(q);
for(int i=1;i<=q;++i)
{
read(e[i].x);
read(e[i].y);
h[i]=e[i].x;
}
sort(h+1,h+q+1);
int tot=unique(h+1,h+q+1)-h-1;
LL t;
for(int i=1;i<=tot;++i)
{
t=(LL)(h[i]-1)*m;
for(int j=1;j<=m;++j) pos[i][j]=++t;
}
for(int i=1;i<=n;++i) last[i]=last[i-1]+m;
int nx;
LL ans;
for(int i=1;i<=q;++i)
{
nx=lower_bound(h+1,h+tot+1,e[i].x)-h;
if(e[i].y==m) ans=last[h[nx]];
else ans=pos[nx][e[i].y];
cout<<ans<<'\n';
if(e[i].y!=m)
{
for(int j=e[i].y;j<m-1;++j) pos[nx][j]=pos[nx][j+1];
pos[nx][m-1]=last[h[nx]];
}
for(int j=h[nx];j<n;++j) last[j]=last[j+1];
last[n]=ans;
}
}
x=1
全部操作只涉及第一行和最后一列
可以开两个数组维护第一行和最后一列
整个过程可以总结为两个操作
1.从序列中找出第k个数并删除
2.把删除的数叫入到另一个序列
我们可以开两棵线段树维护这些信息
#include<cstdio>
#include<vector>
#include<iostream>
#include<algorithm>
using namespace std;
#define N 300001
typedef long long LL;
int n;
int sum[N<<2];
LL a[N<<1];
int sum2[N<<3];
void read(int &x)
{
x=0; char c=getchar();
while(!isdigit(c)) c=getchar();
while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); }
}
void build(int k,int l,int r)
{
sum[k]=r-l+1;
if(l==r) return;
int mid=l+r>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
}
int query(int k,int l,int r,int pos)
{
if(l==r) return l;
int mid=l+r>>1;
if(pos<=sum[k<<1]) return query(k<<1,l,mid,pos);
return query(k<<1|1,mid+1,r,pos-sum[k<<1]);
}
void change(int k,int l,int r,int pos)
{
if(l==r)
{
sum[k]=0;
return;
}
int mid=l+r>>1;
if(pos<=mid) change(k<<1,l,mid,pos);
else change(k<<1|1,mid+1,r,pos);
sum[k]=sum[k<<1]+sum[k<<1|1];
}
void build2(int k,int l,int r)
{
if(l==r)
{
if(l<=n) sum2[k]=1;
return;
}
int mid=l+r>>1;
build2(k<<1,l,mid);
build2(k<<1|1,mid+1,r);
sum2[k]=sum2[k<<1]+sum2[k<<1|1];
}
int query2(int k,int l,int r,int pos)
{
if(l==r) return l;
int mid=l+r>>1;
if(pos<=sum2[k<<1]) return query2(k<<1,l,mid,pos);
return query2(k<<1|1,mid+1,r,pos-sum2[k<<1]);
}
void change2(int k,int l,int r,int pos,int w)
{
if(l==r)
{
sum2[k]=w;
return;
}
int mid=l+r>>1;
if(pos<=mid) change2(k<<1,l,mid,pos,w);
else change2(k<<1|1,mid+1,r,pos,w);
sum2[k]=sum2[k<<1]+sum2[k<<1|1];
}
int main()
{
int m,q;
read(n); read(m); read(q);
build(1,1,m-1);
int i=1; LL j=m;
for(;i<=n;j+=m,++i) a[i]=j;
build2(1,1,n+q);
int x,y; LL ans;
for(int i=1;i<=q;++i)
{
read(x); read(y);
if(y<=sum[1])
{
ans=query(1,1,m-1,y);
cout<<ans<<'\n';
change(1,1,m-1,ans);
change2(1,1,n+q,n+i,1);
a[n+i]=ans;
}
else
{
y-=sum[1];
y=query2(1,1,n+q,y);
cout<<a[y]<<'\n';
change2(1,1,n+q,y,0);
change2(1,1,n+q,n+i,1);
a[n+i]=a[y];
}
}
}
100分
100分和80分其实很相似了,思想上没有太大的变化
想到很多位置都没有动,所以用动态开点线段树
另一个不同点是位置数组需要动态维护,所以开个vector存即可
#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#define RG register
#define il inline
#define iter iterator
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)<(b)?(a):(b))
using namespace std;
typedef long long ll;
const int N=300005,M=6000100;
vector<ll>S[N];
int n,m,Q,tot,root[N],ls[M],rs[M],v[M],cnt=0;
inline void Modify(int &rt,int l,int r,int sa){
if(!rt)rt=++cnt;
v[rt]++;
if(l==r)return ;
int mid=(l+r)>>1;
if(sa<=mid)Modify(ls[rt],l,mid,sa);
else Modify(rs[rt],mid+1,r,sa);
}
inline int qry(int rt,int l,int r,int k){
if(l==r)return l;
int mid=(l+r)>>1;
int sum=mid-l+1-v[ls[rt]];
if(k<=sum)return qry(ls[rt],l,mid,k);
return qry(rs[rt],mid+1,r,k-sum);
}
inline ll caline(int x){
int r=qry(root[n+1],1,tot,x);
Modify(root[n+1],1,tot,r);
return r<=n?1ll*(r-1)*m+m:S[n+1][r-n-1];
}
inline ll calrow(int x,int y){
int r=qry(root[x],1,tot,y);
Modify(root[x],1,tot,r);
return r<m?1ll*(x-1)*m+r:S[x][r-m];
}
void work()
{
int x,y;
ll ret,tmp;
scanf("%d%d%d",&n,&m,&Q);
tot=Max(n,m)+Q;
while(Q--){
scanf("%d%d",&x,&y);
if(y==m){
ret=caline(x);
S[n+1].push_back(ret);
printf("%lld\n",ret);
}
else{
ret=calrow(x,y);
printf("%lld\n",ret);
S[n+1].push_back(ret);
tmp=caline(x);
S[x].push_back(tmp);
}
}
}
int main()
{
freopen("pp.in","r",stdin);
freopen("pp.out","w",stdout);
work();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号