CF1787I Treasure Hunt 题解

CF1787I Treasure Hunt

“*3400 的标算被按在地上摩擦”—— RDFZchenyy。

首先，我们需要把前缀和转为差分。

然后发现答案是形如 \(+-+-\) 或 \(++--\) 的形式。

然后发现 \(t\le q\land s>q\) 的限制是没有用的，因为没有这个限制的话也是 \(++--\)。

然后就可以拆成两部分：所有区间的前缀最大和 \(+\) 所有区间的最大子段和。

前者是简单的，单调栈即可。关键是后者。

低劣的 \(O(n\log n)\) 分治做法

这个思想可以表述为，没有性质，通过“分讨”，硬造性质。然后造性质的代价就是花 log 分治一下。 —— oi tricks。

我们考虑分治。这样只需要考虑跨过区间中点的所有区间的答案。

我们发现，如果固定区间的左端点，右端点向右移动的时候，最大子段和区间是：一开始在左面，后来跨过区间中点，再后来在右面。

我们双指针一下就知道分界点了。知道后随便维护一下即可。

高贵的 \(O(n)\) 做法

考虑直接扫描线。通过打表或者仔细分析可以详细地刻画“右端点一定，左端点取遍 \([1,r]\) 时所有这些区间的最大子段和区间的结构”。

长这样：

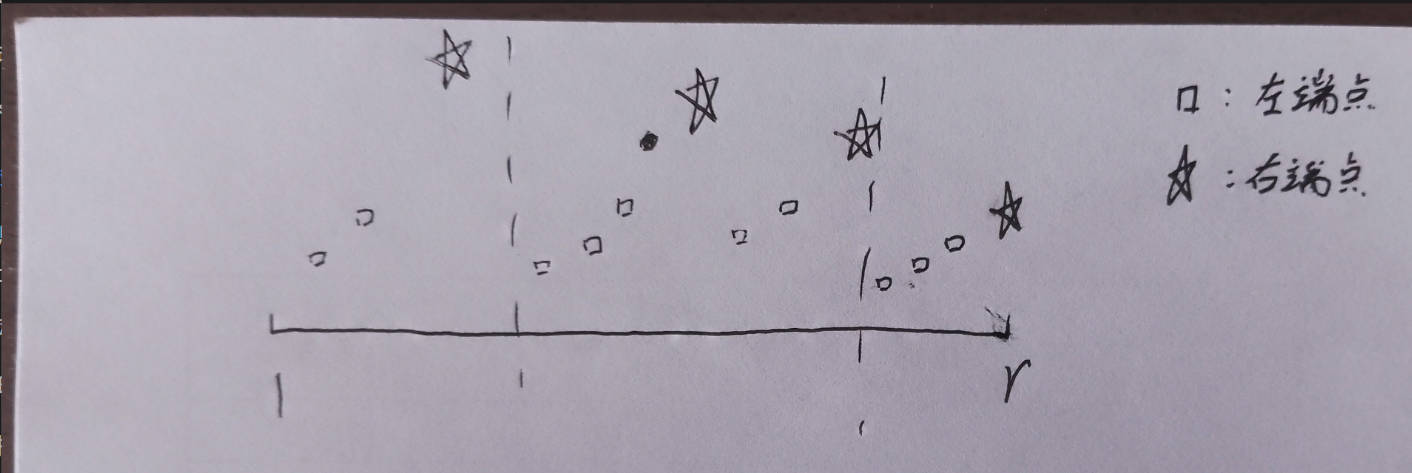
解释一下这个图：我们考虑所有这些结构，它形如：每个虚线段内的右端点和该段内的左端点配对，形成的所有区间。

右端点对应的数是单调递减的，每个段内左端点对应的数是单调递增的。

于是，我们用一个结构维护这样一个段，这个结构本身又在单调栈里。

每次合并的时候有两种情况：

• 单调栈合并：当新来一个星号比上一个星号高，则上一个段没有任何用了，需要把段与段合并。合并的时候，左端点需要“链”起来（一些没有用的左端点会被 pop_back 掉）。

• 最优性合并：当前段和上一个段相比，上一个段末尾的若干元素是没有用的，需要不断 pop_back（注意：有可能导致上一个段被删空，从而导致连锁反应）。

使用 vector 套 list 状物维护，每次使用 a.splice(a.end(),b) 来实现 a+=b 的结果。

以下是不用 std::list 的实现：

const int maxn=1e6+5,mod=998244353;
 
int n,a[maxn];
ll qzh[maxn];
 
ll calc1(){
    qzh[n+1]=LLONG_MAX/3;
    vector<int> stk={n+1};
    ll sum=0,ans=0;
    rev(i,n,0){
        while(qzh[i]>=qzh[stk.back()]) sum-=(stk.end()[-2]-stk.back())*qzh[stk.back()],stk.pop_back();
        stk.pb(i),sum+=(stk.end()[-2]-i)*qzh[i];
        (ans+=sum-(n-i+1)*qzh[i])%=mod;
    }
    return ans;
}
 
int pre[maxn],nxt[maxn];
 
struct List{
    ll sum;
    int high,l,head,tail;
    void pop_back(){
        int tmp=pre[tail];
        if(tmp!=-1) nxt[tmp]=-1;
        pre[tail]=-1;
        tail=tmp;
    }
    vector<int> lst(){
        if(head==-1){
            assert(tail==-1);
            return {};
        }
        assert(pre[head]==-1&&nxt[tail]==-1);
        int x=head;
        vector<int> v;
        debug(head,tail);
        while(x!=tail) v.pb(x),x=nxt[x],debug(x);
        v.pb(tail);
        return v;
    }
    int lastlen()const{return tail+(head==tail? -l+1: -pre[tail]);}
    ll lastgap()const{return qzh[high]-qzh[tail];}
    ll firstgap()const{return qzh[high]-qzh[head];}
    ll getsum()const{return tail==-1? 0: 1ll*(tail-l+1)*qzh[high]-sum;}
};
 
List merge(List a,List b){
    int l=a.l;
    while(a.tail!=-1&&qzh[a.tail]>=qzh[b.head]){
        a.sum-=qzh[a.tail]*a.lastlen();
        b.sum+=qzh[b.head]*a.lastlen();
        a.pop_back();
    }
    b.sum+=a.sum;
    if(a.tail!=-1) pre[b.head]=a.tail,nxt[a.tail]=b.head,b.head=a.head;
    b.l=l;
    return b;
}
 
ll calc2(){
    ll ans=0,sum=0;
    vector<List> v;
    rep(i,0,n) pre[i]=nxt[i]=-1;
    rep(i,0,n){
        v.pb({qzh[i],i,i,i,i}),sum+=v.back().getsum();
        while(v.size()>=2u&&qzh[v.end()[-2].high]<=qzh[v.end()[-1].high]){
            sum-=v.end()[-2].getsum(),sum-=v.end()[-1].getsum();
            List l=merge(v.end()[-2],v.end()[-1]);
            v.pop_back(),v.pop_back();
            v.pb(l),sum+=v.back().getsum();
        }
 
        while(v.size()>=2u){
            if(v.end()[-2].tail==-1){
                v.end()[-2]=v.end()[-1];
                v.pop_back();
            }
            else if(v.end()[-2].lastgap()<=v.end()[-1].firstgap()){
                ll len=v.end()[-2].lastlen();
                sum-=v.end()[-2].getsum(),sum-=v.end()[-1].getsum();
                ll f1=len*qzh[v.end()[-2].tail],f2=len*qzh[v.end()[-1].head];
                v.end()[-2].sum-=f1;
                v.end()[-1].sum+=f2;
                v.end()[-2].pop_back();
                v.end()[-1].l-=len;
                sum+=v.end()[-2].getsum(),sum+=v.end()[-1].getsum();
            }
            else break;
        }
        (ans+=sum)%=mod;
    }
    return ans;
}
 
void solve(){
    cin>>n;
    rep(i,1,n) cin>>a[i],qzh[i]=qzh[i-1]+a[i];
    cout<<(calc1()+calc2())%mod<<endl;
}
 
signed main(){
    cin.tie(0)->sync_with_stdio(0);
    int id,t;
    cin>>t;
    while(t--) solve();
}