ex-deque

不要用冗余的信息消耗你的时空

前言 ex-queue

我们有时候维护一个队列时，会想求其中的信息

如果这个信息具有结合律，那么我们可以做到线性

我们以一道题目为例：

你现在有若干个队列，每个队列初始为空，有以下操作：

• 1 x a11 a12 a21 a22 向第 \(x\) 个队列中 push_back 矩阵 $ \begin{bmatrix} a_{1 1} & a_{1 2} \ a_{2 1} & a_{2 2}\end{bmatrix}$。

• 2 x 第 \(x\) 个队列 pop_front，保证这个队列不为空。

• 3 x 求第 \(x\) 个队列矩阵的乘积（如果队列为空，则输出单位矩阵）。

强制在线

这个问题，显然是可以线段树的

但是，如果我们用线段树维护，就会造成许多的冗余信息，从而导致时间复杂度为 \(O(n\log n)\)

为了避免信息的冗余，我们可以使用以下的结构维护：

struct X{
    vector<pair<int,int>> l,r;
};

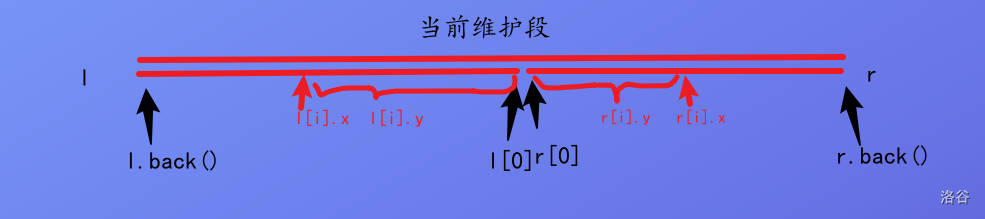
这样，一般情况下，只需要 \(O(1)\) 单次修改

然而，我们有时候会出现 l.empty() 的情况

这时候，我们只需要将 \(r\) 全部转移到 \(l\) 即可，复杂度读者自证不难

ex-deque

有时候，这个 queue 会变成 deque

你现在有若干个队列，每个队列初始为空，有以下操作：

• 1 x a11 a12 a21 a22 向第 \(x\) 个队列中 push_back 矩阵 $ \begin{bmatrix} a_{1 1} & a_{1 2} \ a_{2 1} & a_{2 2}\end{bmatrix}$。

• 2 x a11 a12 a21 a22 向第 \(x\) 个队列中 push_front 矩阵 $ \begin{bmatrix} a_{1 1} & a_{1 2} \ a_{2 1} & a_{2 2}\end{bmatrix}$。

• 3 x 第 \(x\) 个队列 pop_back，保证这个队列不为空。

• 4 x 第 \(x\) 个队列 pop_front，保证这个队列不为空。

• 5 x 求第 \(x\) 个队列矩阵的乘积（如果队列为空，则输出单位矩阵）。

强制在线

这时候，似乎上面的这种结构就无能为力了

不断在上面重构的时候 pop_front，pop_back 即可卡满

然后，我们很自然地想到：重构的时候均匀分配到两个 vector 中

下面证明这个想法的复杂度为 \(O(n)\)

我们定义势能 \(\Phi=|size_l-size_r|\)

每次不重构的时候，只可能至多让势能函数 \(+1\)

重构前，\(\Phi=size_l+size_r\)，重构复杂度为 \(O(size_l+size_r)\)，重构后 \(\Phi=0\)，即 势能减少量等于动能增加量，机械能守恒

可能的实现：

struct Node{
	vector<pair<Mat,Mat>> l,r;
	map<int,int> mp;
	void push_back(Mat x){
		auto pre=(r.empty()?one():r.back().x);
		r.pb({pre*x,x});
	}
	void push_front(Mat x){
		auto pre=(l.empty()?one():l.back().x);
		l.pb({x*pre,x});
	}
	void pop_back(){
		if(r.empty()){
			vector<pair<Mat,Mat>> tmp;
			swap(tmp,l);
			for(int i=(int)(tmp.size()+1)/2;i<(int)tmp.size();i++) push_front(tmp[i].y);
			for(int i=(int)(tmp.size()+1)/2-1;i>=0;i--) push_back(tmp[i].y);
		}
		r.pop_back();
	}
	void pop_front(){
		if(l.empty()){
			vector<pair<Mat,Mat>> tmp;
			swap(tmp,r);
			for(int i=(int)tmp.size()/2;i>=0;i--) push_front(tmp[i].y);
			for(int i=(int)tmp.size()/2+1;i<(int)tmp.size();i++) push_back(tmp[i].y);
		}
		l.pop_back();
	}
	size_t size()const{return l.size()+r.size();}
	Mat calc()const{return (l.empty()?one():l.back().x)*(r.empty()?one():r.back().x);}
}；

merge! split!

有些时候，虽然没有让维护双端队列，但涉及到队列的合并

这对于普通的 ex-queue 来说无能为力，但是 deque 双端可加入的性质就能很好地解决这个问题

可能的实现：

void merge(Node& x){
	if(size()>=x.size()){
		for(int i=x.l.size()-1;i>=0;i--) push_back(x.l[i].y);
		for(auto i:x.r) push_back(i.y);
	}
	else{
		for(int i=r.size()-1;i>=0;i--) x.push_front(r[i].y);
		for(auto i:l) x.push_front(i.y);
		swap(x,*this);
	}
	x={};
}

同理，ex-deque 也支持启发式分裂

应用

• P8496 [NOI2022] 众数

因为摩尔投票具有结合律，因此可以直接套用上面的结构维护，复杂度 \(O(n)\)

值得一提的是，此题不需要平均分配，用 ex-queue 的分裂方式即可

但是，这题难受的一点是还要无解输出 -1，因此再加上 set 启发式合并的复杂度就只能得到 \(O(n\log^2n)\) 的总复杂度了