Lecture 02 Bits, Bytes, and Integer

通过位可以表示集合

例如，一个 \(8\) 位的二进制数 \(01101001\) ，可以用于表示一个全集为 \(\{0,1,2,3,4,5,6,7\}\) 的集合 \(\{0,3,5,6\}\)

• \(01101001\)
• \(76543210\)

通过上面的一一对应关系可以确认集合中的元素。
通过这种表示方法，二进制的位运算可以转换为集合之间的运算：

符号	位运算	集合运算
&	与	交集
|	或	并集
^	异或	对称差
~	非	补集

通过逻辑运算符的短路特性可以避免访问空指针

int *p;
if (p && *p) {
    ...
}

当 \(p\) 为空指针时，会直接返回 \(0\)，当 \(p\) 不为空指针时，才会对 \(*p\) 的值进行判断。

位移运算

当进行位移运算时，向左位移只有唯一一种情况，而向右位移有两种情况，分为逻辑位移和算数位移。两种右位移的区别是填充方式不同。

位移方式	填充
左位移	\(0\)
逻辑右位移	\(0\)
算数右位移	符号位( \(0\) 或 \(1\) )

举例如下：

运算方式	二进制表示
\(x\)	\(01100010\)
<< \(3\)	\(00010000\)
Log.>> \(2\)	\(00011000\)
Arith.>> \(2\)	\(00011000\)

运算方式	二进制表示
\(x\)	\(10100010\)
<< \(3\)	\(00010000\)
Log.>> \(2\)	\(00101000\)
Arith.>> \(2\)	\(11101000\)

补码的实际含义

在有符号整数的计算过程中，将最高位作为负数进行计算，即可直接得到补码，而不需要取反再加一。
用5位数举例如下：

	4	3	2	1	0
原码	16	8	4	2	1
补码	-16	8	4	2	1

• 假设一个数为 \((10110)_2\)，即 \((-10)_{10}\)
• 正常方式计算：补码 \(10110\) \(=>\) 反码 \(10101\) \(=>\) 原码 \(11010\) => \(-8+(-2)=-10\)
• 新算法：补码 \(10110\) => \(-16+4+2=-10\)

通过这种方式可以更好理解补码编码后的极值问题。例如只有 \(5\) 位的情况下，只有第一位表示负数，因此最小的负数一定是 \(10000\)， 而最大的正数一定是 \(01111\)。

无符号整数和有符号整数的转换关系

存在如图的映射关系，其中 \(TMax\) 为有符号整数上限，\(TMin\) 为有符号整数下限，\(UMin\) 为无符号整数上限

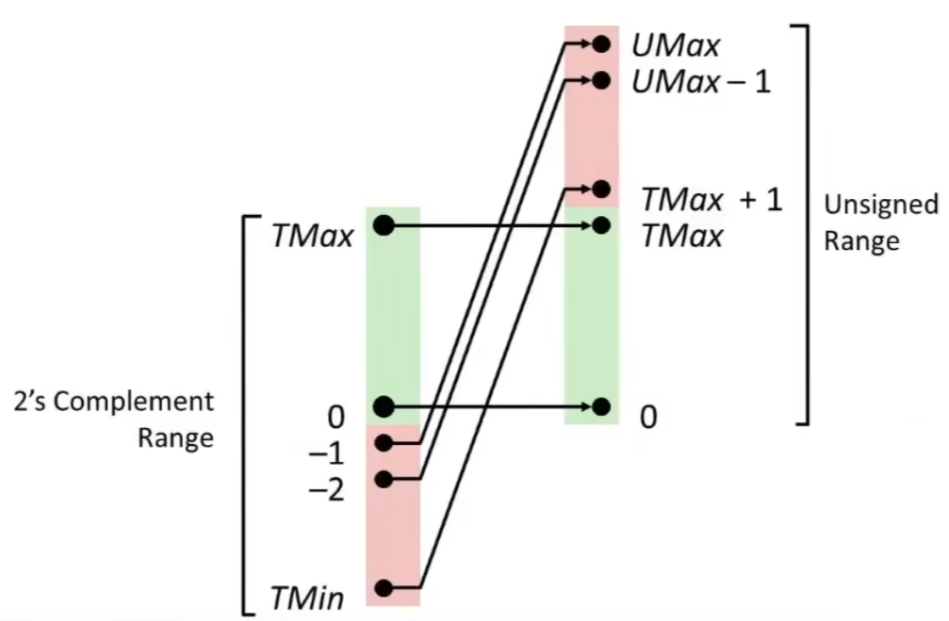
\(UMax=2TMax+1\)的解释

\(TMax=011...1\)
\(2TMax=TMax<<1=11...10\)
\(2TMax+1=11...11=UMax\)

编程时可能出现的问题

当 \(i\) 为无符号整数时
for (i = n - 1; i >= 0; i--) {...}
由于 \(i\) 为 \(0\) 时，再次减一会得到 \(UMax\)，因此该循环将不会结束。
当循环条件中出现sizeof（返回值为size_t，无符号）时容易出现该问题，如：
for (int i = n - 1; i - sizeof(char) >= 0; i--) {...}
此时由于sizeof(char)为无符号，因此运算时 \(i\) 会被转换为无符号整数，循环变为死循环。

符号位拓展

可以使用任意位作为符号位，不会影响数值大小。
当该数为正数时，填充符号位填充的数为 \(0\)，不影响大小。
当该数位负数时，填充符号位填充的数为 \(1\)，假设该数有 \(n\) 位：
计算补码可以发现，新填充的 \(1\) 表示的数为 \(-2^n\)，原本的符号位 \(1\) 表示的数为 \(2^{n-1}\)，两者相加会得到 \(-2^{n-1}\)，与原符号位相同，因此也不影响大小。
举例：

• 原数为 \((0110)_2\)，即 \((3)_{10}\)
• 扩充一位后得到 \((00110)_2\)，\(2+1=(3)_{10}\)
• 原数为 \((1110)_2\)，即 \((-2)_{10}\)
• 扩充一位后得到 \((11110)_2\)，\(-8+4+2+1=(-2)_{10}\)

该操作也解释了右移位时算数移位的意义，即将右移位作为除 \(2^n\) 的除法时，填充 \(1\) 才会得到正确的除法结果。

二进制截断

对于无符号整数，截断二进制的后 \(n\) 位相当于对 \(2^n\) 取模。

• 对于 \((11011)_2\)，即\((27)_{10}，\)截断其后 \(4\) 位，得到 \((1011)_2\)，即 \((11)_{10}\)，相当于对 \(2^4=16\) 取模。
  对于有符号整数，没有计算方面的关联性，但是将其转换为无符号整数后可以进行相同的取模操作。