大一下第二学期期中复习知识梳理 之 c++模板与数据结构

一、函数模板

1.概念

2.声明和定义

声明：必须有形参名，且与定义一致

定义：template<模板参数表> 返回类型 函数模板名（形参表）

 求最大值函数模板应用实例：

#include<iostream>
#include<string>
using namespace std;
template <typename T> T max(T *a,int size)
{
    T temp=a[0];
    for(int i=1;i<size;i++)
    {
        if(a[i]>temp) temp=a[i];
    }
    return temp;
}
int ia[5]={10,7,14,3,25};
double da[6]={10.2,7.1,14.5,3.2,25.6,16.8};
string sa[5]={"上海","北京","沈阳","广州","武汉"};
int main() {
    int i=max(ia,5);
    cout <<"整数最小值为："<<i<<endl;
    double  d=max(da,6);
    cout <<"实数最小值为："<<d<<endl;
    string  s=max(sa,5);
    cout <<"字典排序最小为："<<s<<endl;
    return 0;
}

 

3、函数模板实例化

 1）隐式指定

 例子：

定义一次之后已经生成相关类型的函数，等下次再使用相同类型的函数时可以同时使用。

  2）显式指定

 例子：

3）矩阵转置/相乘函数模板应用实例

一维数组类型：与长度有关。

二维数组类型： 由数据最低维度确定 ： 同：相同类型：eg：a[2][4]与b[3][4] ，都由4决定；异：不同类型：eg：a[2][3]与b[2][4]，一个为3一个为4. 

矩阵乘法类型变化: T1([2][4])*T2([3][4])=T2([2][3]).

多维数组类型：由最高位之后整体维度确定：eg：a[3][4][1]与b[3][4][2]不同类；a[5][4][3]与b[10][4][3]同类。

#include<iostream>
#include<iomanip>
using namespace std;
template<typename T1,typename T2>
void inverse(T1 *mat1,T2 *mat2,int t1,int t2)
{
	for(int i=0;i<t2;i++)
		for(int j=0;j<t1;j++)
			mat2[j][i]=mat1[i][j];
}
template<typename T1,typename T2>
void multi(T1 *mat1,T2 *mat2,T2 *mat3,int t1,int t2,int t3)
{
	for(int i=0;i<t3;i++)
		for(int j=0;j<t2;j++)
			for(int k=0;k<t1;k++)
		mat3[k][i]=mat2[j][i]*mat1[k][j];
}
template<typename T>
void output(T *mat,char *a,int t1,int t2)
{
	cout<<a<<endl;
	for(int i=0;i<t1;i++)
		{{for(int j=0;j<t2;j++)
		cout<<setw(4)<<mat[i][j];}
	cout<<endl;}
}
int main()
{
int middle[6][3], result[6][4];
int matrix1[3][6]={8,10,12,23,1,3,5,7,9,2,4,6,34,45,56,2,4,6}; 
int matrix2[3][4]={3,2,1,0,-1,-2,9,8,7,6,5,4};
char *s1="result", *s2="middle";
inverse(matrix1,middle,6,3); 
//显式：inverse<int[6],int[3]> (matrix1,middle,6,3);
multi(middle,matrix2,result,6,3,4); 
//显式：multi <int[3],int[4]> (middle,matrix2,result,6,3,4);
output(matrix1, "matrix1", 3, 6);
output(middle, s2, 6, 3);
output(matrix2, "matrix2", 3, 4);
output(result, s1, 6, 4);
	return 0;
}

　　

4、函数模板和函数重载异同

 

 

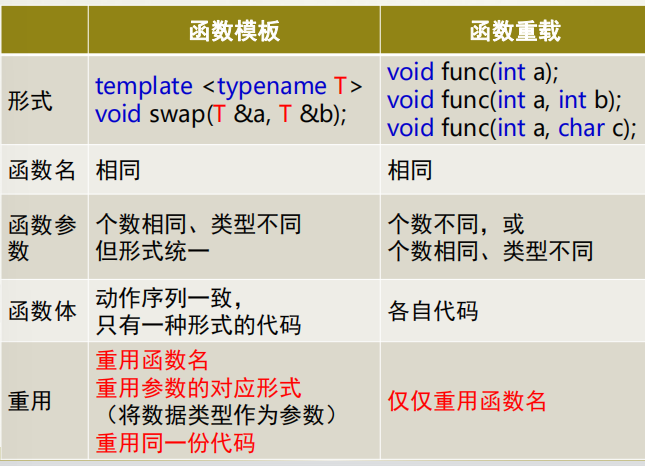
 注意：函数模板定义时要明白哪些类型，使得这些类型都可实现。重用参数非所有数据类型都可以。

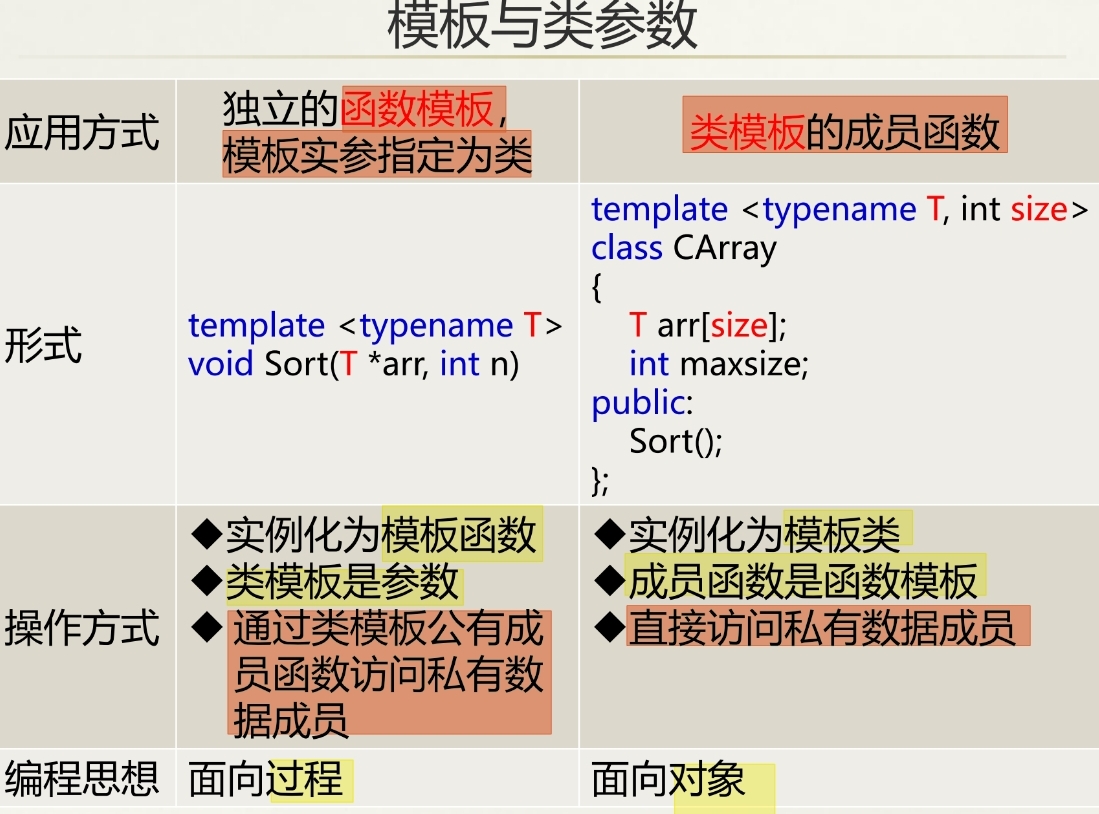
二、类模板

1.概念

具有相同特征的类族。 类名相同, 成员构成相同

2.定义：

template<模板参数表>

定义类；

（类模板内可定义非类模板的成员函数，但此必须在类内写完；类模板外定义的成员函数必须是函数模板）

template<模板参数表>

函数类型名 类模板名 <模板参数名>:: 函数名（函数参数表）｛｝

size在类模板中用作常量，不可在后续成员函数中修改。

例如：

3.模板实例化

4.

三、线性表

（一）概念

（二）分类

按访问方式分类：

顺序表（数组）：直接随机访问

链表：间接顺序访问

队列：双端单向访问；链队，顺序队 

栈：单端双向访问；链栈，顺序栈

（三）顺序表

1.概念

直接随机访问的线性表

元素顺序排列（如数组元素顺序连续排列），

通过下标访问——访问元素(读写已知位置)的时间开销与表长度无关

2.属性

数据表（数组）：开大空间，以空间换存储使用便利性，大开小用

表头位置：通常为0；表尾未知：任意位置；表长=表尾位置－表头位置+1=表尾位置+1(表头为0时)。最大表长=数组大小。

3.操作

（1）表长计算与表空满判断

（2）下标操作

（3）查找元素位置

（4）插入元素：时间开销与表的长度（后面元素个数，到表尾为止）有关（成正比），必须是顺序操作（防止数据被覆盖）

（5）删除元素：时间开销与表的长度（后面元素个数，到表尾为止）有关（成正比），必须是顺序操作（防止数据被覆盖）

4.实现:顺序表类模板实例

封装成类的形式

#include<iostream>
using namespace std;
template<typename T,int size>
class seqlist
{
private:
    T m_list[size];   //存放顺序表的数组
    int m_max_size;  //最大可容纳元素个数
    int m_last;  //表尾元素位置:为最后一个有效数值的位置
public:
//构造函数：初始化为空表(不能用默认构造函数)
seqlist()
{m_last=-1; m_max_size=size;}
//计算表长度：表长=表尾位置-表头位置+1;最大表长=数组大小 .const:表示常函数（在此函数中不能对类任何数据成员修改）
int Length() const 
{return m_last+1;}
//判断表是否空：判断m_last位置，若表长=0，则m_last+1==0，即m_last==-1.
bool isempty() const 
{return m_last==-1;}
//判断表是否满
bool isfull() const
{return m_last==m_max_size-1;}
//取第i个结点，注意判断i值合理性
T Get(int i)  
{return i<0||i>m_last?NULL:m_list[i];}
//重载下标运算符[]
T& operator[](int i);
//寻找x在表中位置
int Find(T &x)const;
//判断x是否在表中
bool IsIn(T &x)const;
//寻找x的后继位置（下标）
int Next(T &x)const;
//寻找x的前驱位置（下标）
int Prior(T &x)const;
//x插入到列表中的i位置（下标）
bool Insert(T &x,int i);
//删除x
bool Remove(T &x);
};
//下标操作（运算符[]重载）：返回地址，带&可作为左值使用。
template<typename T,int size>
T & seqlist<T,size>::operator[](int i)
{
    if(i==m_last+1) m_last++;
else if(i<0||i>m_last||i>=m_max_size)
    {
     cout<<"下标出界！"<<endl;
     exit(1);
    }
    return m_list[i];
}
//查找元素位置：从前向后逐个比对
template<typename T,int size>
int seqlist<T,size>::Find(T &x)const
{
    int i=0;
    while(i<=m_last&&m_list[i]!=x) i++;
if(i>m_last) return -1;
else return i;
}
//判断元素是否在表中
template<typename T,int size>
bool seqlist<T,size>::IsIn(T &x)const
{
    int i=0;
    bool found=0;
    while(i<=m_last&&!found) 
if(m_list[i]!=x) i++;
else found=1;
return found;
}
//插入操作:从后往前：固定头尾，第一次m_list[last]=m_list[last-1]，最后一次m_list[i+1]=m_list[i].
template<typename T,int size>
bool seqlist<T,size>::Insert(T &x,int i)
{
    int j;
    if(i<0||i>m_last+1||m_last==m_max_size-1) return false;
    else
    {
        m_last++;
for(int j=m_last;j>i;j--)
            m_list[j]=m_list[j-1];
        m_list[i]=x;
        return true;
    }
}
//删除操作：从前往后：固定头尾；第一次m_list[i]=m_list[i+1],最后一次m_list[m_last]=m_list[m_last+1].
template<typename T,int size>
bool seqlist<T,size>::Remove(T &x)
{
    int i;
    i=Find(x);
    if(i>=0)
    {
        m_last--;
        for(int j=i;j<=m_last;j++)
            m_list[j]=m_list[j+1];
        return true;
    }
    return false;
}
//查找前驱元素位置：表头无前驱
template <typename T,int size>
int seqlist<T,size>::Prior(T &x) const
{
    int i=Find(x);
    if(i>0&&i<=m_last) return i-1;
    return -1;
}
//查找后继元素位置：表尾无后继
template <typename T,int size>
int seqlist<T,size>::Next(T &x) const
{
    int i=Find(x);
    if(i>=0&&i<m_last) return i+1;
    return -1;
}
int main()
{
    seqlist <int,100> seqlisti; //顺序表对象seqlisti的元素为整型
    int i,j,k,a[10]={2,3,5,7,11,13,17,19,23,29};
    for(j=0;j<10;j++)
    if (!seqlisti.Insert(a[j],j)){//把素数写入
    cout<<"数据太多表放不下了!"<<endl; break;}
    j=seqlisti.Length();
    for(i=0;i<j;i++) cout<<seqlisti.Get(i)<<' '; //2 3 5 7 11 13 17 19 23 29
    cout << endl ;
    for(j=0;j<10;j++) seqlisti[j]=0; //采用下标运算符运算
    for(j=0;j<10;j++) cout<<seqlisti[j]<<' '; //0 0 0 0 0 0 0 0 0 0
    cout<<endl;
    for(j=0;j<10;j++) seqlisti[j]=a[j];
    seqlisti[10]=31; //实验能否增加元素
    for(j=0;j<11;j++) cout<<seqlisti[j]<<' '; //2 3 5 7 11 13 17 19 23 29 31
    cout<<endl;
    k=7;
    if (seqlisti.IsIn(k)) cout<<"素数7在顺序表中"<< endl; //素数7在顺序表中
    //因形参为引用，所以实参不可用整数常量7
    else cout <<"素数7不在顺序表中"<<endl;
    k=17;
    if (seqlisti.Remove (k)) cout<<"删除素数17"<<endl; //删除素数17
    else cout<<"找不到素数17，无法删除";
    j=seqlisti.Length( ) ;
    for (i=0;i<j;i++) cout<<seqlisti.Get(i)<<' '; //2 3 5 7 11 13 19 23 29 31
    cout<<endl;
    if (seqlisti.Insert(k,j-1)){ // 把素数17装回去,成功则打印
    j=seqlisti.Length ( );
    for (i=0;i<j;i++) cout<<seqlisti.Get(i)<<' '; 
    cout<<endl;} //2 3 5 7 11 13 19 23 29 17 31
    return 0;
}

操作算法：

查找元素：从前向后，逐个比对

插入元素：从后向前，逐个后移

删除元素：从前向后，逐个前移

四、排序算法

思想：使顺序序列叠加顺序元素个数依次增多

双重循环：外循环：遍历所有元素；内循环：遍历所有可能性

（一）插入排序（直接插入排序）

template <typename T, int size> 
void Orderedlist<T,size>::InsertSort(){ //升序
T temp; //暂存待插入数据
int i, j;
for (i=1;i<=last;i++){ //注意从i=1开始，只做last轮
temp=slist[i]; //第i轮插入slist[i]，先暂存到temp
j=i; //j是插入位置，初始值是i
while (j>0&& temp<slist[j-1]){ //从后向前找到插入位置j
slist[j]=slist[j-1]; //如果不是即将j-1数据后移
j--; //依次往前
}
slist[j]=temp; //插在位置j
}
}

（二）交换排序

 （三）冒泡排序

template <typename T, int size> 
void Orderedlist<T,size>::BubbleSort(){
bool noswap; //为真时表示本轮未发生交换，可结束排序
int i, j; T temp;
for (i=0;i<last;i++){ //最多做last-1轮
noswap=true; //默认为真，发生交换后置为假
for (j=last;j>i;j--){ //从底至首，两两比较
if (slist[j]<slist[j-1]){ //发现逆序对
temp=slist[j];slist[j]=slist[j-1];slist[j-1]=temp; //交换
noswap=false; //标记发生交换
}
}
if (noswap) break; //本轮未发生交换，结束排序
}
}

（四）直接选择排序（选择排序）

1、选择排序

 2、直接选择排序

template <typename T, int size> 
void Orderedlist<T>::SelectSort(){
int i,j,k; T temp;
for(i=0;i<last;i++){ //做last-1轮
k=i; //最小元素下标，初始值i
temp=slist[i]; //最小元素，初始值slist[i]
for (j=i;j<=last;j++) //找出真正的最小元素
if (slist[j]<temp){ //发现比temp小的，替换之
k=j;
temp=slist[j];
}
if(k!=i) //最小元素(k)与未排序首元素(i)交换
temp=slist[i]; slist[i]=slist[k]; slist[k]=temp;
}
}