51nod 1284

//给出一个数N，求1至N中，有多少个数不是2 3 5 7的倍数。
#include<iostream>
using namespace std;
int main()
{long long n;
long long sum=0;
cin>>n;
sum+=(n/2+n/3+n/5+n/7);
sum-=(n/6+n/10+n/14+n/15+n/21+n/35);
sum+=(n/30+n/42+n/70+n/105);
sum-=(n/210);              //先计算出1到n中有多少数是2 3 5 7的倍数，利用了容斥原理求2 3 5 7倍数的并集
cout<<n-sum;
}

容斥原理是一种重要的组合数学方法，可以让你求解任意大小的集合，或者计算复合事件的概率。

描述

       容斥原理可以描述如下：

         要计算几个集合并集的大小，我们要先将所有单个集合的大小计算出来，然后减去所有两个集合相交的部分，再加回所有三个集合相交的部分，再减去所有四个集合相交的部分，依此类推，一直计算到所有集合相交的部分。

关于集合的原理公式

      上述描述的公式形式可以表示如下：
       

 

        

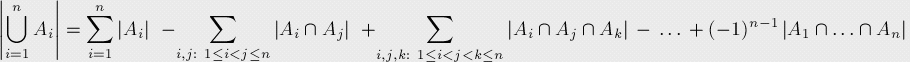
关于维恩图的原理

       用维恩图来表示集合A、B和C：

       

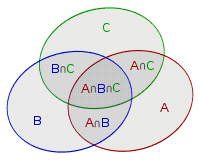
         那么的面积就是集合A、B、C各自面积之和减去 , ,  的面积，再加上的面积。

         由此，我们也可以解决n个集合求并的问题。