用集合说明可以用与或非来表示异或

用集合说明可以用与或非来表示异或

异或（XOR，记作 A⊕B）可以通过与（AND，记作 ∧）、或（OR，记作 ∨）、非（NOT，记作 ¬）的组合来表示。以下是两种常见的表达式形式：

1. 直接组合形式

异或的逻辑可以描述为：当且仅当 A 和 B不同时为真时输出真。

即：

A	B	A⊕B
0	0	0
0	1	1
1	0	1
1	1	0

所以可以表示为下图形式

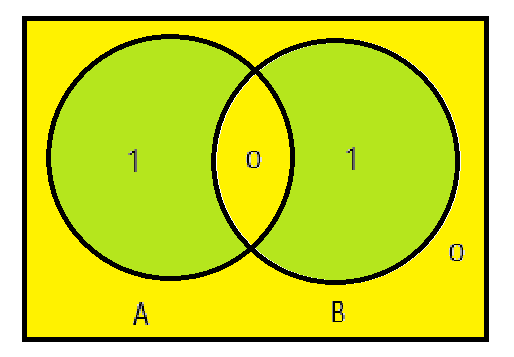
通过集合可以很清楚的得到对应的逻辑表达式为：

A⊕B = (A∧¬B) ∨ (¬A∧B)

而通过这个逻辑表达式可以说明：

异或可以通过与或非来表示

2. 全加器C_out的表达式

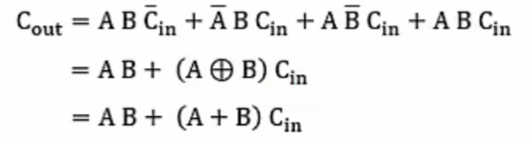
注意后两个等式，说明的不是A⊕B等于A+B ，而是AB+(A⊕B)C_in = AB+(A+B)C_in ，

因为 AB + (A ⊕ B)C_in = **AB + ABC_in + (A ⊕ B)C_in ** = AB+(A+B)C_in

---

学习视频

• 021_运算方法和运算电路_全加器和并行加法器_哔哩哔哩_bilibili