简读||Signals With Sparse Mutual Interference for Sounding Massive MIMO Channels

原文链接：https://ieeexplore.ieee.org/document/9424581

摘要

摘要：提出了新的探测参考信号（SRS），针对信道老化（aging）的时分双工，大规模MIMO。提出的SRS之间是稀疏的，即有零相关区（ZCZ）。仿真中通过峰均功率比（PAPR）来衡量SRS的性能，并给出构建低PAPR的SRS方法。

关键词

关键词：大规模 MIMO、探测参考信号(SRS)、信道老化（aging）、零相关区(ZCZ)。

一、介绍

  SRS常用来接收端估计信道脉冲响应（CIR），用于上行链路（UL）的基站（BS），也可以利用蜂窝系统的互易性转换成下行链路（DL）的CIR，并估计DL的预编码，预编码可以使得DL的CIR估计无需UE的CSI反馈。当UL和DL信号的时间间隔较大时，通过SRS估计出的UL－CIR与DL数据的时间差别过大，性能下降。现有的研究应对信道老化的方法复杂度高且假设在理想信道，不能完全解决问题。

  另一种方法是使用更短的SRS间隔，当SRS成对正交且对互非零延迟也是零成对互相关，但SRS正交对的增多会占用信息传输的时频资源。

  有研究提出，使用不同功率的非正交SRS实现短周期，离BS近的UE是强UE，发射更少的功率，使远近两个UE接收信号的功率大致相同。对于近UE，远UE的信号功率强，可以串行干扰消除（SIC），对于远UE，近UE功率小可认为小噪声忽略。最后BS根据两个UE的CIR选出相同的预编码，选出二者DL信息的重合。非正交SRS造成更多的CIR估计错误，而CIR的估计错误又减少了可降低信道老化的公共预编码数量。

二、系统模型和基础信息

  TDD　OFDM　ｍMIMO系统由一个NA天线的BS和E用户的单天线用户组成，N个子载波且等间隔（SCS），信道是一般的多径信道，信道互易性成立，信道系数随着UE的移动而变化，具有信道老化特征。

信道互易性：基本思想是利用无线信道互易性建立共享密钥，即一个无线链路的发射器和接收器可以同时观察同一信道。上行方向的信道估计可以直接用于下行链路的链路自适应。由于TDD系统中上下行链路在相同的频率上进行传输，当上下行的发送时间间隔足够短时，可认为上行信道与下行信道的衰落基本相同，即TDD系统中上下行信道具有互易性。UL发送SRS，BS运算能力强来计算CSI，通过互易性，在DL直接使用CSI。

A、定时提前机制

  定时提前机制（TA）就是不同UE可以提前传输信息，使得BS接收时各UE的信号时域对齐。

B、UL SRS 传输

  假设所有UE的CIR的最大延迟都小于OFDM符号的循环前缀（CP）长度，BS的第$r$个天线接收到的信号为：

$$\begin{aligned}{y_{r}}^{(UL,o)}(k)&=\sum_{e=0}^{E_{0}-1}\sum_{m=0}^{L_{max}-1}h_{e,r}^{(o)}(m)s_{e}(k-m)+{z_{r}}^{(UL,o)}(k) \\&=\sum_{e=0}^{E_{0}-1}\sum_{m=0}^{L_{max}-1}h_{e,r}^{(o)}(m)s_{e}((k-m)\ \textrm{mod }\ N)+{z_{r}}^{(UL,o)}(k) \end{aligned}\tag{1}\label{f1}$$

  这里的$h_{e,r}^{(o)}(m)$是第$r$个天线，第$e$个用户，第$o$个OFDM符号的信道脉冲响应CIR，假设每个OFDM符号的$h_{e,r}^{(o)}(m)$是相同的，不同符号间的$h_{e,r}^{(o)}(m)$是变化的（信道老化）。${z_{r}}^{(UL,o)}(k)$是独立同分布的AWGN。

C、UL信道估计

  BS收到SRS后通过匹配滤波器生成CIR，参考信号{$s_{e}^{*}(k)$}匹配滤波器的输出：

$$\begin{aligned}\theta _{y_{r},s_{e}}(p)&\\ &=\sum_{k=0}^{N-1}s_{e}^{*}(k)y_{r}^{(UL,o)}((k+p)\ mod \ N)\\ &=\sum_{e^{'}=0}^{E_{0}-1}\sum_{m=0}^{L_{max}-1}h_{e^{'},r}^{(o)}(m)\sum_{k=0}^{N-1}s_{e}^{*}(k)s_{e^{'}}(k)((k+p-m)\ mod\ N)+\sum_{k=0}^{N-1}s_{e}^{*}(k)z_{r}^{(UL,o)}((k+p)\ mod\ N)\\ &=\sum_{m=0}^{L_{max}-1}h_{e,r}^{(o)}(m)\theta _{s_{e},s_{e}}(p-m)+\sum_{e^{'}=0,e^{'}\neq e}^{E_{0}-1}\sum_{m=0}^{L_{max}-1}h_{e^{'},r}^{(o)}(m)\theta _{s_{e^{'}},s_{e}}(p-m)+\tilde{z}_{e,r}^{(UL,o)}(p)\end{aligned}\tag{2}\label{f2} $$ $$\begin{aligned}\theta _{s_{e^{'}},s_{e}}(p)=\sum_{k=0}^{N-1}s_{e}^{*}(k)s_{e^{'}}(k)((k+p)\ mod\ N)\end{aligned}\tag{3}\label{f3} $$

  \eqref{f3}是周期互相关函数，当$e^{'}=e$时变为周期自相关函数。$\tilde{z}_{e,r}^{(UL,o)}(p)=\sum_{k=0}^{N-1}s_{e}^{*}(k)z_{r}^{(UL,o)}((k+p)\ mod\ N)$是匹配滤波器输出的噪声。

相关：$\int_{-\infty }^{\infty }s_{1}(t)s_{2}^{*}(t-\tau )dt=\int_{-\infty }^{\infty }s_{1}(t+\tau)s_{2}^{*}(t )dt$

卷积：$f(t)*g(t)=\int_{-\infty }^{\infty }f(\tau)g(t-\tau )d\tau=\int_{-\infty }^{\infty }f(t-\tau)g(\tau)d\tau$

  SRS的有长度为$D_{ZAZ}$的零自相关区（ZAZ）\eqref{f4}，不同的SRS间具有长度为$D_{ZCCZ}$的零互相关区（ZAZ）\eqref{f5}

$$ \begin{aligned}\theta _{s_{e},s_{e}}(p)=\begin{cases}=0, & \left| p\right|=1,2,...,D_{ZAZ} \\ \neq 0,& p= D_{ZAZ}+1 \ \textup{or} -(D_{ZAZ}+1) \end{cases}\end{aligned}\tag{4}\label{f4} $$ $$\begin{aligned}\theta _{s_{e^{'}},s_{e}}(p)=\begin{cases}=0, & \left| p\right|=1,2,...,D_{ZCCZ} \\ \neq 0,& p= D_{ZCCZ}+1 \ \textup{or} -(D_{ZCCZ}+1) \end{cases}\end{aligned}\tag{5}\label{f5} $$

  ZAZ和ZCCZ中最小的区域称为零相关区（ZCZ），当$D_{ZCZ}\geqslant L_{max}$且检测时间窗口$p$满足$L_{max}\leqslant D \leqslant D_{ZCZ}+1$，\eqref{f2}简化成为：

$$\begin{aligned}\theta _{y_{r},s_{e}}(p)=\begin{cases}h_{e,r}^{(o)}(p)\theta_{s_{e},s_{e}}(0)+\tilde{z}_{e,r}^{(UL,o)}(p),& 0\leqslant p< L_{max} \\ \tilde{z}_{e,r}^{(UL,o)}(p),& L_{max}\leqslant p< D \end{cases}\end{aligned}\tag{6}\label{f6} $$

  给定$D_{ZCZ}$的最大用户数（SRS数）为$\frac{N}{D_{ZCZ}+1}$，当用户数过多时采用时分复用（TDM）重复利用SRS，这样会导致更长的SRS和信道老化。

D、DL数据发送

  BS向第$e$个UE发送OFDM符号$d_{e}^{(o^{'})}(f)$，符号被分配到第$f$个子载波上，$N_{A}$个BS天线的预编码向量$v_{e,0}^{(o^{'})}(f),...,v_{e,N_{A}-1}^{(o^{'})}(f)$，发送信号：

$$\begin{aligned}x_{e,r}^{(o^{'})}(k)=\frac{1}{\sqrt{N}}\sum_{f=0}^{N-1}v_{e,r}^{(o^{'})}(f)d_{e}^{(o^{'})}(f)W_{N}^{-kf}\end{aligned}\tag{7}\label{f7} $$

  $W_{N}=e^{-\sqrt{-1}2\pi /N}$，BS发送信号时加入了循环前缀（CP），UE收到的信号为：

$$\begin{aligned}{y_{e}}^{(DL,o^{'})}(k)=\sum_{r=0}^{N_{A}-1}\sum_{m=0}^{L_{max}-1}h_{e,r}^{(o^{'})}(m)x_{e,r}^{(o^{'})}(k-m)+{z_{e}}^{(DL,o^{'})}(k)\end{aligned}\tag{8}\label{f8} $$

  发送给其他用户对接收信号的干扰被省略。在\eqref{f7}中预编码是基于最新估计出的UL CIR，使用DFT变换到频域，然后计算预编码：

$$\begin{aligned}\hat{H}_{e,r}^{(o)}(f)=\frac{1}{\sqrt{N}}\sum_{m=0}^{L_{max}-1}\hat{h}_{e,r}^{(o^{'})}(m)W_{N}^{fm}\end{aligned}\tag{9}\label{f9}$$ $$\begin{aligned}v_{e,r}^{(o^{'})}(f)=\frac{(\hat{H}_{e,r}^{(o)}(f))^{*}}{(\sum_{r^{'}=0}^{N_{A}-1}\left| \hat{H}_{e,r^{'}}^{(o)}(f)\right|^{2})^{1/2}}\end{aligned}\tag{10}\label{f10}$$

三、稀疏相关性的SRS

  $QA$SRS包含$Q$个SRS子集，每个子集里面有$A$个SRS，表示为$s_{q,n}(k)$，由DFT生成:

$$\begin{aligned}s_{q,n}(k)=\frac{1}{\sqrt{N}}\sum_{f=0}^{N-1}S_{q,n}(f)W_{N}^{-kf}\end{aligned}\tag{11}\label{f11}$$ $$\begin{aligned}S_{q,n}(f)=\begin{cases}W_{N}^{\Delta _{q}f}c_{q,n}(Ai+l), & f=\delta i+j_{l}\in \bar{\Omega} \\ 0,& else \end{cases} \end{aligned}\tag{12}\label{f12}$$

  其中$\bar{\Omega}$有块重复结构，$N=\delta t$，$t$个子带各有$\delta$个子载波。在子带中找$A$个相同子载波去构建$\bar{\Omega}$

$$\begin{aligned}\bar{\Omega}=\{\left.\begin{matrix}\delta i+j_{l} \end{matrix}\right|i=0,1,...,t-1,l=0,1,...,A-1\}\end{aligned}\tag{13}\label{f13}$$

  每个子带中不重合的$A$个子载波，可以构建$\left \lfloor \delta /A\right \rfloor$正交交织。不同交织上的SRS彼此正交互不影响。\eqref{f12}中的单位幅度序列$c_{q,n}(u)$总长度为$At$

$$\begin{aligned}c_{q,n}(u)=b_{q,n}(u\ mod\ A)a(u)\end{aligned}\tag{14}\label{f14}$$

  $b_{q,n}(l)$是短序列，长度为$A$，在相同的第$q$个子集中是正交的。$a(u)$是长序列，长度为$At$取值任意。相位旋转$\Delta _{q}$是第$q$子集的SRS实现时域循环偏移，不同子集的周期互相关函数也会相应偏移，在匹配滤波器的输出处可以减轻相互干扰。

$$\begin{aligned}0\leq \Delta _{0}<\Delta _{1}<...<\Delta _{Q-1}<t\end{aligned}\tag{15}\label{f15}$$ $$\begin{aligned}\Delta _{q}=q\left \lfloor t/Q\right \rfloor,\ q=0,1,...,Q-1\end{aligned}\tag{16}\label{f16}$$ $$\begin{aligned}\Delta _{q}=\left \lfloor qt/Q\right \rfloor,\ q=0,1,...,Q-1\end{aligned}\tag{17}\label{f17}$$

  \eqref{f16}和\eqref{f17}是为了让非零互相关值远离零互相关值

A、相关性质

  定理1：\eqref{f11}-\eqref{f14}构建的SRS周期自相关$D_{ZAZ}\geq t-1$

  定理2：\eqref{f11}-\eqref{f17}构建的SRS周期互相关，两个SRS来自同一正交SRS子集时$D_{ZCCZ}\geq t-1$；来自不同正交SRS子集时$D_{ZCCZ}\geq \left \lfloor t/Q\right \rfloor-1$

  在生成的SRS集合中，每个SRS子集的ZCZ有$D_{ZCZ}=t-1$，对于整个SRS集合，有$D_{ZCZ}=\left \lfloor t/Q\right \rfloor-1$

B、对CIR估计的影响

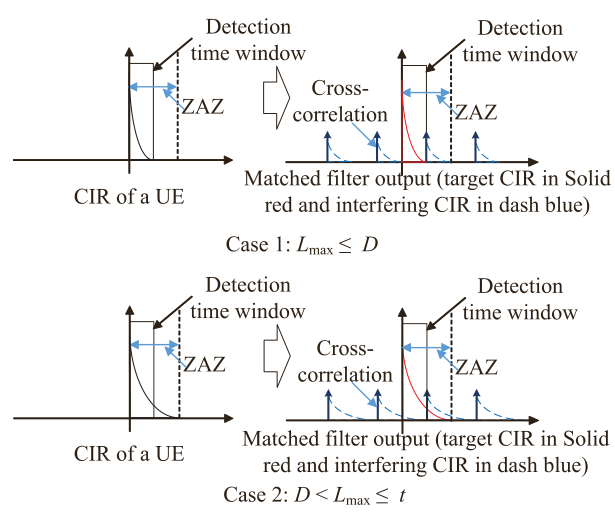
  来自相同SRS子集的并发SRS，当$L_{max}\leq t$时，设置时间检测窗口$D= min\begin{Bmatrix} L_{max},t\end{Bmatrix}$可以保证无干扰CIR估计。由定理1和定理2可知，不同SRS接收的间隔最小为$\left \lfloor t/Q\right \rfloor$。来自不同SRS子集的SRS信号，检测窗口$D= min\begin{Bmatrix} L_{max},\left \lfloor t/Q\right \rfloor\end{Bmatrix}$可以实现无干扰CIR估计。当$L_{max}\leq \left \lfloor t/Q\right \rfloor$时，如图中情况1，CIR信息没有被干扰；当$L_{max}> \left \lfloor t/Q\right \rfloor$时，如图中情况2，只有其他SRS信号的尾部有干扰，但是可以忽略。当信道抽头不在CIR前端首部时，只要所有SRS都被分配给相似CIR的UE时（不同的CIR可以通过正交交织消除干扰），结论仍然成立。BS只需要移动窗口覆盖主要的信道抽头就能估计出CIR。

四、SRS的实施

A、参数设置和参考方案

  以$N$个子载波的妹1/4作为参考（Comb-4），NR的SRS由12个等距线性相位旋转的ZC序列（Zaddoff Chu，ZC）生成。取$A=12,\delta =48$。设置SRS子集数量$Q$，SRS总数大于等于UE的数量：

$$\begin{aligned}Q=\left \lceil E/A\right \rceil\end{aligned}\tag{18}\label{f18}$$

B、短序列构造

  在\eqref{f14}中，第$q$个子集的短序列$b_{q,n}(l)$，把其作为$A\times A$的DFT序列的不同列，逐元素乘长度为$A$的序列。

C、长序列构造

  长序列取值任意，可以用来优化生成SRS的PAPR，最小PAPR的长序列$a(u)$是可调制恒幅度零自相关序列（CAZAC），只在$t\ mod\ A=0$时存在：

$$\begin{aligned}a(iA+l)=\eta (l)g_{l}(i\ mod\ t/A)W_{t}^{\mu (l)i}\end{aligned}\tag{19}\label{f19}$$

CAZAC：长度为$L$的序列在除了零延迟之外的所有延迟偏移处都具有恒定幅度和零周期性自相关。

$$x_{u}(n)=e^{-j\frac{\pi un(n+1)}{N-1}}$$

  $\eta (l)$是单位幅度序列，$\mu (l)$是置换函数，$g_{l}$是CAZAC。对于$t\ mod\ A\neq 0$，只能构建次优的SRS。

  方法1：

$$\begin{aligned}a(iA+l)=\eta (l)g_{l}(i\ mod\ s_{l})W_{t^{'}}^{\mu (l)i}\end{aligned}\tag{20}\label{f20}$$

  对于\eqref{f20}，有三种实现方法，并给出了PAPR

  方法2：

$$\begin{aligned}a(u)=exp(-\sqrt{-1}\frac{\pi ru(u+1)}{N_{ZC}})\end{aligned}\tag{25}\label{f25}$$

五、仿真结果

六、结论